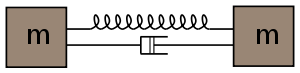
Masse-Feder-System (Computergrafik)

Ein mögliches Anwendungsgebiet des Masse-Feder-Systems ist die Darstellung korrekter physikalischer Materialeigenschaften wie bei diesem Modell, das mit Blender erstellt wurde.

Das Masse-Feder-System (kurz MFS, englisch Mass-Spring-System), in der Literatur auch Masse-Feder-Modell (kurz MFM), ist ein Verfahren in der Computergrafik, um das Deformationsverhalten von auf Polygonnetzen basierenden Objekten zu bestimmen. Es kann sowohl auf ebene, als auch auf räumliche Objekte angewandt werden.

Die Gründe für die weite Verbreitung des Masse-Feder-Systems sind das leichtverständliche physikalische Konzept, die einfache Implementierung und die relativ niedrigen Rechenanforderungen.^[1]

Geschichte

Das Masse-Feder-System basiert auf den physikalischen Ansätzen des Hookeschen Gesetzes.

Aufgrund der geringen Rechenleistung früherer Computer wurde es nur für Flächen genutzt (sowohl zweidimensionale, als auch im dreidimensionalen Raum eingebettete Flächen, zum Beispiel ein Tischtuch, das über einen Tisch fällt). Deshalb wurde es bei seinen ersten Verwendungen ab dem Jahr 1981 zunächst nur zur Haut- und Stoffverhaltenssimulation verwendet.^[2][3] Erst 1989 wurden die ersten MFS-Volumenmodelle veröffentlicht.^[4][5]

Heute ist es ein gängiges Verfahren in der Computerspielbranche und in der Medizin^[1] zur Simulation operativer Eingriffe.

Aufbau

Zwei Masseknoten, die mit einer Feder und einem Dämpfer verbunden sind.

In einem Masse-Feder-System werden Objekte durch ein Netz aus Masseknoten, mechanischen Federn und Dämpfungsgliedern dargestellt.^[2][6]

Ablauf der Verschiebung eines Punktes in einem Masse-Feder-System zu verschiedenen Zeitpunkten.

Die Knoten eines Polygonnetzes bekommen jeweils eine Masse. Die Kanten werden durch eine mechanische Feder, die mit einem Dämpfungsglied parallel geschaltet ist, dargestellt. Somit hat sie eine Federkonstante, eine Ruhelänge und eine Abklingkonstante. Das Dämpfungsglied ist notwendig, wenn das Objekt nach der Deformation nicht schwingen sondern eine Ruhelage finden soll. In Abhängigkeit der Masseknoten wird der Reibungskoeffizient errechnet.

Die Masseknoten sind regelmäßig im ganzen Objekt verteilt und stellen es so dar. Zur Verbindung der Masseknoten werden Federn zwischen sie gesetzt. Sind zwei Masseknoten miteinander verbunden, nennt man sie benachbart. Die Ausgangsform des Objekts liegt vor, wenn alle Federn in Ruhelage sind (E_pot = 0), also deren Ruhelänge haben. Wird nun ein Masseknoten verschoben, liegt an den benachbarten Federn eine potentielle Energie an ($E_{pot} \neq 0$), die nun durch Verschieben der benachbarten Massepunkten minimiert wird. Eine solche Verschiebung wirkt sich auf das ganze Netz aus, wodurch sich dieses verschiebt.

Um einer Verschiebung im Raum entgegenzuwirken, können Punkte „befestigt“ werden (an einer absoluten Position oder an einer relativen Position zu einem anderen Massepunkt).^[6] Dadurch kann unter anderem eine plastische Deformation erzielt werden.

Das Masse-Feder-System kann, um physikalisches Verhalten realistischer zu machen, um eine Kollisionserkennung ergänzt werden, damit die Massepunkte auf Kollisionen untereinander und auf Kollisionen mit anderen Objekten reagieren können.

Berechnung

In der folgenden Herleitung wird von einem d-dimensionalen Raum ausgegangen.

Masse-Feder-Systeme haben ihren Ursprung in der klassischen Mechanik. Sie basieren auf der Idee, dass ein Körper M durch einen einzelnen Masseknoten m repräsentiert werden kann. Weitergehend kann dieser Masseknoten in n kleinere Masseknoten m_i, verteilt über den ganzen Körper, unterteilt werden, sodass gilt:

$m=\sum \limits_{i=1}^{n} m_i$

Nach dem Hookeschen Gesetz ist das Verhalten einer Feder mit parallelem Dämpfungsglied folgendermaßen definiert:

$\vec F_s = -k \cdot \vec s - \mu \cdot \dot{\vec s}$

wobei k die Federkonstante, $\vec s$ die Auslenkung der Feder zur Ruhelage und μ der Reibungskoeffizient ist.

Newtons Definition zum Verhalten einer bewegten Masse ist:

$\vec F = m \cdot \vec a$

$\vec F$ ist die Kraft, die dem Körper der Masse m die Beschleunigung $\vec a$ erteilt.

Auf Basis dieser letzten beiden Gleichungen kann die Bewegungsgleichung eines einzelnen Masseknotens i hergeleitet werden.

Auf den Masseknoten i mit der Masse m_i wird bei der Verschiebung um $\vec s_i \in \mathbb{R}^d$ die Kraft $\vec F_i$ ausgeübt:

$\vec F_i = m_i \cdot \ddot{\vec s_i}$

Die Auslenkung $\vec s_{ij}$ wird bei zwei Masseknoten i und j in einem Masse-Feder-System mit der Distanz voneinander abzüglich der Länge der Feder im Ruhezustand l_0,ij berechnet:

$\vec s_{ij} = \frac{\vec x_j - \vec x_i}{\begin{vmatrix}\vec x_j - \vec x_i\end{vmatrix}} \cdot (\begin{vmatrix}\vec x_j - \vec x_i \end{vmatrix} - l_{0,ij})$

$\vec x_i$ ist die Position des i-ten Masseknotens. Mit $\frac{\vec x_j - \vec x_i}{\begin{vmatrix}\vec x_j - \vec x_i\end{vmatrix}}$ wird der Richtungsvektor als Einheitsvektor von Masseknoten i zu Masseknoten j berechnet. Der Betrag von $\begin{vmatrix}\vec x_j - \vec x_i\end{vmatrix} - l_{0,ij}$ ist der Abstand zwischen Masseknoten i und Masseknoten j minus der Ruhelänge der Feder, was den Längenskalar darstellt. Das Skalarprodukt $\vec s_{ij}$ ist die Auslenkung des Masseknotens i in Abhängigkeit vom Masseknoten j.

Das führt zu folgender Kraft, die auf den einzelnen Masseknoten i mit dem benachbarten Knoten j wirkt:

$\vec F_{s,ij} = -k_{ij} \cdot \vec s_{ij} -\mu_{ij} \dot{\vec s_i}$

Die externen Kräfte, die auf den Masseknoten i wirken, können als $\vec F_{ext,i}$ zusammengefasst werden:

$\vec F_{ext,i} = \vec F_{G,i} + \vec F_{e,i}$

mit dem Vektor der äußeren Kraft $\vec F_{ext,i}$, dem Gravitationsvektor $\vec F_{G,i}$ und dem Vektor der anderen externen Einwirkungen $\vec F_{e,i}$.

Fasst man alle auf den Masseknoten i wirkenden Kräfte zusammen, erhält man folgende Differenzialgleichung als Bewegungsgleichung, wobei N die Menge der benachbarten Masseknoten ist:

$\vec F_{i} = \sum \limits_{j \in N}\vec F_{s,ij} + \vec F_{ext,i}$

Es gilt $\vec F_i = m_i \ddot{\vec s_i}$:

$m_i \ddot{\vec s_i} = \sum \limits_{j \in N}\vec F_{s,ij} + \vec F_{ext,i}$

Die Bewegungsgleichung für das gesamte System erhält man, indem man alle Verschiebungen s_i mit dem Vektor $\vec s = (\vec s_1, \vec s_2, ..., \vec s_n)^T$, die Massen m_i mit der Matrix M, die Reibungskoeffizienten μ_ij mit der Matrix D und die Federkonstanten k_ij der einzelnen Masseknoten durch die Matrix K beschreibt: ^[1]

$\vec F_{ext} = M \cdot \ddot{\vec s} + D \cdot \dot{\vec s} + K \cdot \vec s$

Die Matrizen D und K sind beide symmetrisch, da μ_ij = μ_ji und k_ij = k_ji. Daraus folgt, dass jeweils nicht alle n² Komponenten, sondern nur $\frac{n^2+3n}{2}$ Komponenten berechnet werden müssen. Außerdem können die Komponenten auf der Hauptdiagonalen der Matrizen D und K (also die Komponenten μ_ii und k_ii) vernachlässigt werden, da es keine Feder gibt, die an beiden Enden mit demselben Masseknoten verbunden ist. Die Anzahl der zu berechnenden Komponenten verringert sich somit auf $\frac{n^2+n}{2}$.

Siehe auch

• Federpendel
• Harmonischer Oszillator

Weblinks

•  Commons: Masse-Feder-Systeme – Sammlung von Bildern, Videos und Audiodateien
• Beispiele zum Masse-Feder-System von Johan Jansson
• Max-Planck-Institut – MEDUSA erweckt virtuelle Gesichter zum Leben

Einzelnachweise

1. ↑ ^{a b c} Markus A. Schill: Biomechanical Soft Tissue Modeling Techniques, Implementation and Applications. Universität Mannheim, Mannheim 2001 (Dissertation, PDF, 24,6MB, abgerufen am 1. Juli 2011).
2. ↑ ^{a b} S. Platt, N. Badler: Animating Facial Expressions. In: Computer Graphics. 15, Nr. 3, 1981 (PDF).
3. ↑ K. Waters: A Muscle Model for Animating Three-Dimensional Facial Expression. In: Computer Graphics. 21, Nr. 4, 1987 (Link).
4. ↑ J. Chadwick, D. Haumann, R. Parent: Layered Construction for Deformable Animated Characters. 1989 (PDF).
5. ↑ D. Terzopoulos, K. Waters: Physically-based Facial Modelling, Analysis and Animation. 1, 1990 (PDF).
6. ↑ ^{a b} Jens Neumann: Verfahren zur adhoc-Modellierung und -Simulation räumlicher Feder-Masse-Systeme für den Einsatz in VirtualReality-basierten Handhabungssimulationen. Technische Universität Berlin, Fraunhofer IRB Verlag, 2009, ISBN 978-3-8167-7954-4 (Dissertation).