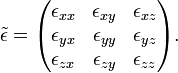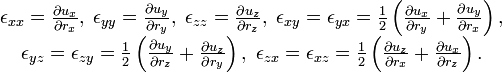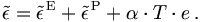Elastizitätstheorie

Die Kontinuumsmechanik ist das Teilgebiet des theoretischen Bauingenieurwesens, Maschinenbaus und der Physik, das vom Verformungsverhalten verschiedener Substanzen handelt.

Übersicht

In der Kontinuumsmechanik wird vom mikroskopischen Aufbau der Materie, also zum Beispiel der Gitterstruktur kristalliner Festkörper und der molekularen Struktur von Flüssigkeiten, abgesehen und der Untersuchungsgegenstand als ein Kontinuum genähert.

Eine grundlegende Einteilung der Kontinuumsmechanik basiert auf der Unterscheidung zwischen elastischer (reversibler) und plastischer (irreversibler) Deformation oder Verformung. Bei Überschreitung des plastischen Fließvermögens kommt es zum Bruch des Festkörpers oder zum Zerreißen der Flüssigkeit. Bei der Deformation einer Flüssigkeit ist die Oberflächenspannung zu berücksichtigen.

Die Elastizitätstheorie (siehe Elastizität (Mechanik)) beruht auf dem verallgemeinerten Hookeschen Gesetz, das einen linearen, tensoriellen Zusammenhang zwischen einer Verspannung und der daraus resultierenden Verzerrung des Kontinuums herstellt.

Plastische Verformungen (Plastizität) werden in der Rheologie und der Strömungslehre näher untersucht.

Die mathematische Struktur der Elastizitätstheorie weist erhebliche Ähnlichkeit mit der Strömungslehre auf; zur Beschreibung viskoelastischer Materialien können beide Theorien miteinander vereinigt werden.

Beschreibung von Verzerrungen

Die mechanischen Eigenschaften eines Materials können als der mathematische Zusammenhang zwischen Spannungen und Verzerrungen ausgedrückt werden. Im einfachsten Fall, beschrieben durch das Hookesche Gesetz, ist dieser Zusammenhang linear: Die Verformung eines Materials ist linear zu einer angelegten äußeren Kraft.

Ausgangspunkt der Kontinuumsmechanik ist somit die mathematische Beschreibung von Verzerrungen und Spannungen.

Unter einer Verzerrung oder Deformation versteht man in der Physik die Veränderung der gegenseitigen Lagebeziehungen der Materieelemente. Diese Änderung der inneren Anordnung korrespondiert mit einer Änderung der äußeren Gestalt des Festkörpers.

Ein Spezialfall der elastischen Verformung ist die Dehnung eines Stabs in Längsrichtung. Naiv könnte man meinen, dass sich dieser Spezialfall eindimensional durch einen linearen Zusammenhang zwischen ausgeübter Kraft und resultierender Längenänderung beschreiben lässt. Tatsächlich aber führt die ausgeübte eindimensionale Belastung bereits zu einer mehrdimensionalen Verzerrung, da sich auch der Durchmesser des Stabs ändert (Querkontraktion). Deshalb ist selbst in den einfachsten Fällen eine dreidimensionale, tensorielle Beschreibung von Verzerrungen erforderlich.

Wir betrachten eine Verzerrung, die ein Materieelement aus einem Punkt r in einen Punkt r`=r+u transportiert hat. Dieser Sachverhalt lässt sich durch ein Vektorfeld u(r) ausdrücken. Ein konstantes Feld u(r)=c entspricht einer Translation des Festkörpers als ganzem; ein Feld u(r)=A r (mit einer orthogonalen Matrix A) entspricht einer Drehung. Solche Verschiebungen bewirken keine innere Verzerrung. Eine Verzerrung tritt nur dann auf, wenn benachbarte Materieelemente in unterschiedlicher Weise verschoben werden; wenn sich also u(r) und u(r+dr) voneinander unterscheiden. Die Verformung des einzelnen Materieelements kann deshalb durch die partiellen Ableitungen der Komponenten von u nach den Komponenten von r beschrieben werden. Diese Ableitungen bilden den Verzerrungstensor

$\tilde\epsilon= \begin{pmatrix} \epsilon_{xx} & \epsilon_{xy} & \epsilon_{xz} \\ \epsilon_{yx} & \epsilon_{yy} & \epsilon_{yz} \\ \epsilon_{zx} & \epsilon_{zy} & \epsilon_{zz} \end{pmatrix}.$

Seine Komponenten lauten

$\begin{matrix} &\epsilon_{xx}=\frac{\partial u_x}{\partial r_x},\; \epsilon_{yy}=\frac{\partial u_y}{\partial r_y},\; \epsilon_{zz}=\frac{\partial u_z}{\partial r_z},\; \epsilon_{xy}=\epsilon_{yx}=\frac12\left(\frac{\partial u_x}{\partial r_y}+ \frac{\partial u_y}{\partial r_x}\right),\\ &\epsilon_{yz}=\epsilon_{zy}=\frac12\left(\frac{\partial u_y}{\partial r_z}+ \frac{\partial u_z}{\partial r_y}\right),\; \epsilon_{zx}=\epsilon_{xz}=\frac12\left(\frac{\partial u_z}{\partial r_x}+ \frac{\partial u_x}{\partial r_z}\right). \end{matrix}$

Die Symmetriebeziehungen ε_xy = ε_yx usw. folgen aus der Forderung, dass Drehungen des gesamten Körpers unberücksichtigt bleiben sollen. Deshalb hat der Verzerrungstensor nur sechs unabhängige Komponenten.

Beschreibung von Spannungen

siehe einstweilen den Artikel Mechanische Spannung.

Verzerrungs-Spannungs-Beziehungen

Die lineare elastische Deformation

Siehe:

• Hookesches Gesetz
• Energieelastische Deformation

Die nichtlineare elastische Deformation

Bei der nichtlinearen elastischen Deformation ist die Verschiebung benachbarter Punkte des Kontinuums nicht proportional zum Abstand dieser Punkte. Die nichtlineare elastische Deformation kann beispielsweise an Gummi beobachtet werden, in diesem Zusammenhang spricht man von Gummielastizität oder auch Entropieeleastizität. In diesem Fall kann das Hookesche Gesetz nicht angewandt werden. Diese Situation ist in der Natur die Regel. Wo möglich wird versucht, dieses Problem in einer linearen Näherung zu behandeln. Insbesondere für kleine Deformationen ε ist diese Näherung häufig gerechtfertigt.

Die plastische Deformation

In realen Medien ist jede Deformation nur bis zu einer gewissen Grenze elastisch. Wird diese Grenze überschritten, so tritt bei duktilen Materialien plastische Deformation (Plastisches Fließen) auf. Bei der plastischen Deformation kehrt der Körper mit dem Ausbleiben der für die Deformation verantwortlichen mechanischen Belastung nicht wieder in seine Ausgangsform zurück. In diesem Fall genügt die Angabe der Positionen von Punkten des Festkörpers nicht mehr zur Kennzeichnung des Zustands des Festkörpers, sondern es muss auch der Prozess berücksichtigt werden, d. h. 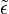$\tilde\epsilon$ ist in diesem Fall keine Zustandsgröße.

Im allgemeinen Fall kann die Deformation durch 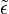$\tilde\epsilon$ angegeben werden. Die Gesamtdeformation 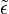$\tilde\epsilon$ setzt sich aus einem elastischen Anteil 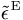$\tilde\epsilon^{\,\rm E}$, einem plastischen Anteil 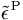$\tilde\epsilon^{\,\rm P}$ und dem temperaturbedingten Anteil zusammen:

$\tilde\epsilon = \tilde\epsilon^{\,\rm E} + \tilde\epsilon^{\,\rm P} + \alpha \cdot T \cdot e\,.$

Elastisch-plastisches Materialverhalten kann beschrieben werden durch eine Fließbedingung, ein Fließgesetz, und ein Verfestigungsgesetz.

Fließbedingung

Die Fließbedingung legt all diejenigen mehrachsigen Spannungszustände fest, an denen das Material plastisch fließt. Es ist üblich, die Fließbedingung als eine konvex gekrümmte Fläche im Spannungsraum anzugeben, die Fließortfläche heißt. Für Spannungszustände innerhalb des von der Fließortfläche umschlossenen Raums deformiert das Material rein elastisch. Liegt der aktuelle Spannungszustand auf der Fließortfläche, so kann plastisches Fließen eintreten. Spannungszustände außerhalb des umschlossenen Raums sind bei elasto-plastischen Materialverhalten unmöglich.

Gebräuchliche Fließbedingungen für metallische Werkstoffe wurden von Huber, von Mises und Tresca formuliert. Ihnen liegt die Annahme isotropen Verhaltens zu Grunde.

Die Fließbedingung nach R. v. Mises lautet:

$0 = \frac{3}{2} \tilde{s}^T\cdot\tilde{s} - k_{\rm f}^2$,

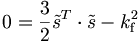wobei 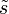$\tilde{s}$ den Spannungsdeviator und k_f die Streckgrenze bezeichnet. Der Spannungsdeviator ist der um den hydrostatischen Anteil reduzierte Spannungstensor

$\tilde{s}=\sigma-p\cdot e\ \textrm{mit}\ p = \frac{\sigma_x + \sigma_y + \sigma_z}{3}$.

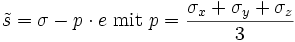Nach Tresca ist die Fließbedingung:

$0 = \frac{\sigma_I-\sigma_{II}}{2}- k$,

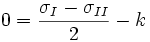k_f = σ_I − σ_II

mit σ_I und σ_II der größten bzw. kleinsten Hauptnormalspannung. Für eine graphische Interpretation der Trescaschen Regel können die Mohrschen Spannungskreise herangezogen werden.

Beide Formulierungen werden häufig angewendet. Die Regel von v. Mises ist im allgemeinen Fall einfach anzuwenden. Wenn die Lage des Hauptachsensystems bekannt ist, wird oft mit der Trescaschen Regel gerechnet. Für numerisches Rechnen hat diese die Nachteile, dass jeweils eine Hauptachsentransformation nötig ist und dass die Fließortfläche nicht stetig differenzierbar ist.

Fließgesetz

Das Fließgesetz bestimmt die plastischen Verzerrungsinkremente. Im Falle assoziierter Plastizität ist dieses Inkrement coaxial zum Normalenvektor der Fließortfläche am aktuellen Spannungsort. Die Größenordnung des Inkrements bestimmt der skalarwertige plastische Multiplikator.

Im Falle nicht-assoziierter Plastizität bedient man sich zur Festlegung der plastischen Verzerrungsrichtung häufig eines für diesen Zweck definierten plastischen Potentials. Man kann den assoziierten Fall also auch als den Spezialfall auffassen, bei dem plastisches Potential und Fließbedingung dieselbe Fläche im Spannungsraum projizieren.

Verfestigungsgesetz

Das Verfestigungsgesetz legt fest, auf welche Weise die Fließbedingung während des Fließens modifiziert wird. Idealisiert kann von zwei unterschiedlichen Verfestigungsverhalten ausgegangen werden, dem isotropen und kinematischen Verfestigen.

Durch isotropes Verfestigen kann das Materialverhalten beschrieben werden, wenn es von der vorhergehenden Belastungsrichtung unabhängig ist, bzw. wenn sich die Belastungsrichtung nicht ändert. Das isotrope Verfestigen wird durch Expansion der Fließortfläche ausgedrückt. Das heißt, die Streckgrenze k_f steigt abhängig von der aufgebrachten Verformung um einen gewissen Betrag an.

Durch kinematisches Verfestigen kann zum Beispiel der Bauschingereffekt beschrieben werden, d.h. die Streckgrenze ist bei Belastung in Gegenrichtung deutlich niedriger als während der vorherigen Belastung. Dieses Phänomen kann durch Verschieben der Fließortfläche beschrieben werden. Die Streckgrenze k_f bleibt dabei konstant, es verändert sich nur der "Mittelpunkt des Fließorts" (back stress) 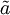$\tilde{a}$. In der Fließregel muss dann die Fließspannung durch die „reduzierte Spannung” 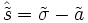$\hat{\tilde s}=\tilde\sigma-\tilde{a}$ ersetzt werden.

Homogenität

Auf atomarer Ebene sind die physikalischen Eigenschaften der Materie nicht homogen sondern ortsabhängig, und zwar unabhängig, ob es sich dabei um ein Gas, eine Flüssigkeit, oder einen Festkörper handelt. Beispielsweise Massedichte, oder auch Ladungsdichte variieren zwischen den Materiebausteien (Moleküle eines Gases, Ionenrümpfe eines Kristallgitters, Elektronen des Leitungsbands, etc.), und schon diese Bausteine selbst können im Allgemeinen nicht als homogen betrachtet werden.

In der Praxis können diese Schwankungen auf atomarer Ebene jedoch häufig vernachlässigt werden, und Materie kann als homogen angesehen werden, wenn sie in ihren Eigenschaften auf makroskopischen Längenskalen gleichförmig ist.

Isotropie

Auf atomarer Ebene gilt zur Isotropie Vergleichbares wie zur Homogenität: Von einem Materiebaustein aus gesehen treten im Allgemeinen in verschiedenen Richtungen unterschiedliche Nachbarn in unterschiedlichen Abständen auf. Dadurch entsteht generell Richtungsabhängigkeit (Anisotropie). Auf makroskopischer Betrachtungsebene können sich diese Unregelmäßigkeiten aber wieder herausmitteln, sodass der Körper auf dieser Ebene als isotrop angesehen werden kann.

Eine Besonderheit stellen Kristalle dar. Die der Gitterstruktur entsprechende, richtungsabhängige Anordnung der elementaren Bausteine tritt hier regelmäßig auf. Sie kann deshalb auch makroskopisch observiert werden. Selbiges gilt für das konstitutive Verhalten von aus Kristallen aufgebauten Körpern. Aus Gittersymmetrien ergeben sich zusätzliche Bedingungen. Zum Beispiel hat ein Kristall mit hexagonaler Kristallstruktur in Richtung der c-Achse (das ist die sechszählige Achse des Hexagons) eine unterschiedliche Festigkeit als senkrecht dazu. Da sich aber metallische Werkstoffe aus einer Vielzahl von Kristallen zusammensetzen (die werden dann Kristallite genannt), ist die makroskopisch messbare Anisotropie von der Vorzugsrichtung der Kristallite abhängig.

Fließen

Die Deformation findet nicht homogen im gesamten Material, sondern nur an energetisch bevorzugten Kristallbaufehlern wie Versetzungen, Phasengrenzen und amorphen Einlagerungen statt.

Literatur

• Arnold Sommerfeld: Mechanik der deformierbaren Medien, Leipzig : Becker & Erler, 1945. - Vorlesungen über theoretische Physik ; Band 2 (6. Auflage, Harri Deutsch, Thun 1992, ISBN 3-87144-375-1)

Siehe auch

• Hookesches Gesetz
• Konfiguration (Mechanik)
• Beobachtung
• Verformung
• Plastizitätstheorie

Weblinks

• Lehr- und Forschungsgebiet Kontinuumsmechanik, Prof. Itskov, RWTH Aachen