Feynmans verschollene Vorlesung: Die Bewegung der Planeten um die Sonne

Feynmans verschollene Vorlesung ist ein Buch über eine von Richard Feynman gehaltene Physik-Vorlesung über die Bewegung der Planeten um die Sonne.

Die Vorlesung, um die es hier geht, hat Richard Feynman am 13. März 1964 am California Institute of Technology nach eigener Aussage zum Vergnügen der Studenten gehalten. Sie gehörte nicht mehr zum Prüfungsstoff und hatte keinen Eingang in das dreibändige Werk “Feynman-Vorlesungen über Physik” gefunden. 1992 konnte die Archivarin Judith R. Goodstein eine Tonbandaufnahme und einige von Feynman angefertigte Skizzen sicherstellen und anschließend zusammen mit ihrem Mann, dem Physiker David. L. Goodstein, diese als verschollen geglaubte Vorlesung rekonstruieren. Daraus ist das 1996 bei W. W. Norton & Company erschienene Buch Feynman's Lost Lecture entstanden, es wurde von Anita und Jürgen Ehlers ins Deutsche übersetzt.

Nach einem kurzen historischen Rückblick von Copernicus zu Newton und einigen biographischen Anmerkungen zu Richard Feynman wird Feynmans von Goodstein rekonstruierter und in allen Details ausgearbeiteter Beweis des Ellipsensatzes dargestellt, schließlich wird die Vorlesung selbst im Wortlaut wiedergegeben. In der amerikanischen Ausgabe liegt das vorhandene Tondokument auch als CD bei.

Es wird ausgeführt, wie Newton auf Basis des dritten keplerschen Gesetzes das richtige Abstandsgesetz zu seinem Gravitationsgesetz fand und dann umgekehrt auf Basis dieses Gravitationsgesetzes und seiner Mechanik die keplerschen Gesetze hergeleitet hatte. Dabei ist der Ellipsensatz, nach dem sich die Planeten auf elliptischen Bahnen um die Sonne bewegen, der schwierigste Teil. Feynman erwähnte, dass auch Newton in den Philosophiae Naturalis Principia Mathematica einen rein geometrischen Beweis dargelegt hatte, dabei aber Argumente über Kegelschnitte verwendet hatte, die ihm (Feynman) nicht geläufig seien. Er habe den Beweis daher auf eine eigene Weise zu Ende gebracht. Genau dieser Beweis steht im Mittelpunkt des Buches. Er zeichnet sich dadurch aus, dass er elementar ist in dem Sinne, dass nur Mathematik der Sekundarstufe I verwendet wird. Dennoch wird der Beweis als nicht einfach bezeichnet.

Skizze zur beschriebenen Ellipsenkonstruktion

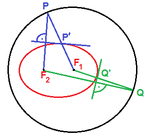
Ausgehend von der Definition einer Ellipse als Menge aller Punkte, die von zwei vorgegebenen Punkten, den sogenannten Brennpunkten, eine konstante Abstandssumme haben (Gärtnerkonstruktion), wird hergeleitet, dass ein von einem Brennpunkt ausgehender Lichtstrahl von der Ellipsenlinie in den anderen Brennpunkt reflektiert wird. Daraus ergibt sich folgendes Konstruktionsverfahren einer Ellipse aus einem vorgegebenen Kreis: Neben dem Kreismittelpunkt F₁ wird ein weiterer Punkt F₂ aus dem Kreisinneren als Brennpunkt ausgezeichnet. Zu jedem Punkt P der Kreislinie konstruiert man dann den Bildpunkt P^' als Schnittpunkt aus der Strecke $\overline{F_1P}$ und der Mittelsenkrechten zur Strecke $\overline{F_2P}$. Die Menge aller so konstruierten Bildpunkte ergibt eine Ellipse. Das ist dann später die entscheidende geometrische Tatsache in Feynmans Argumentation, die von einem Geschwindigkeitsdiagramm der Planetenbewegung auf die Ellipsenform der Bahn schließt. Feynman nennt als Quelle seiner Beweisidee eine Arbeit von U. Fano über die Rutherfordsche Streuformel, letztere wird im abschließenden Teil der Vorlesung ebenfalls ausgeführt.

Literatur

• David L. Goodstein, Judith R. Goodstein: Feynmans verschollene Vorlesung. Die Bewegung der Planeten um die Sonne, Piper Verlag GmbH (1998), ISBN 3-492-03922-7
• David L. Goodstein, Judith R. Goodstein: Feynman's Lost Lecture. The Motion of Planets Around the Sun, W. W. Norton & Company (1996), ISBN 0-393-03918-8