Liouville-Funktion

Die Liouville-Funktion, benannt nach Joseph Liouville, ist eine multiplikative zahlentheoretische Funktion. Sie wird mit dem griechischen Buchstaben λ bezeichnet und ist wie folgt definiert:

$\lambda(n)=(-1)^{\Omega(n)},\,$

wobei Ω(n) die Anzahl der (nicht notwendigerweise verschiedenen) Primfaktoren bezeichnet.

Man definiert außerdem λ(0) = 0 und λ(1) = 1.

Die ersten Werte (beginnend bei n = 1) sind

1, -1, -1, 1, -1, 1, -1, -1, 1, 1, -1, -1, -1, 1, 1, 1, -1, -1, -1, -1, ...^[1]

Eigenschaften

Es gilt^[2]

$\sum_{d|n}\lambda(d)=\begin{cases} 1, \qquad \mathrm{wenn}\; n\; \mathrm{eine\; Quadratzahl\; ist} \\ 0,\qquad\mathrm{sonst}\end{cases}$

Die Liouville-Funktion ist verwandt mit der Möbius-Funktion μ durch^[3]

$\lambda(n)=\sum_{d^2|n} \mu\left(\frac{n}{d^2}\right)$

Reihen

Die Dirichlet-Reihe der Liouville-Funktion lässt sich durch die riemannschen Zeta-Funktion ζ ausdrücken:^[4]

$\sum_{n=1}^\infty \frac{\lambda(n)}{n^s}=\frac{\zeta(2s)}{\zeta(s)}$

Ihre Lambert-Reihe ist gegeben durch

$\sum_{n=1}^\infty \frac{\lambda(n)q^n}{1-q^n}=\sum_{n=1}^\infty q^{n^2}=\frac12(\vartheta_3(q)-1)$

wobei $\vartheta_3$ die Jacobische Theta-Funktion bezeichnet.

Summen

Es sei

$L(n)=\sum_{k=1}^n \lambda(k).$

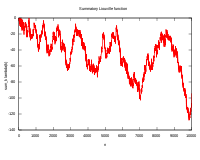
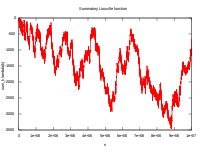
• Graphen von L(n)
• 

  L_n bis n=10.000

• 

  und bis 10⁷ (anderer Maßstab!)

Die Pólya-Vermutung besagt, es sei – wie die Grafiken oben vermuten ließen – stets^[5]

$L(n)\le 0.$

Diese Vermutung wurde mittlerweile widerlegt; das kleinste Gegenbeispiel ist n = 906150257. Es ist bisher allerdings nicht bekannt, ob L sein Vorzeichen unendlich oft wechselt.

Eine verwandte Summe ist

$M(n)=\sum_{k=1}^n \frac{\lambda(k)}k.$

Für diese wurde vermutet, sie sei für hinreichend große n stets positiv; dies wurde von Haselgrove^[6] widerlegt, wobei er zeigte, dass M unendlich oft negative Werte annimmt. Ein Beweis der Vermutung hätte die Richtigkeit der riemannschen Vermutung zur Folge.^[7]

Referenzen

1. ↑ Folge A008836 in OEIS, vgl. Folgen A026424 und A028260
2. ↑ Liouville Function auf PlanetMath
3. ↑ http://eom.springer.de/L/l059620.htm
4. ↑ R. S. Lehman: On Liouville's Function In: Math. Comput. 14, 1960, S. 311-320
5. ↑ Eric W. Weisstein: Polya Conjecture. In: MathWorld. (englisch)
6. ↑ C.B.Haselgrove: A disproof of a conjecture of Polya. Mathematika 5 (1958), S. 141–145.
7. ↑ Hisanobu Shinya: On an arithmetical approach to the Riemann hypothesis, 23. Juni 2009, arXiv:0906.4155

1. Eric W. Weisstein: Liouville Function. In: MathWorld. (englisch)