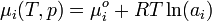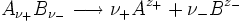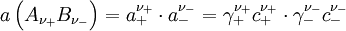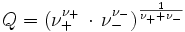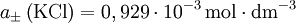- Chemische aktivität
-
Die Aktivität oder die thermodynamische Aktivität ist eine konzentrationsabhängige, dimensionslose Größe in der physikalischen Chemie. Die Aktivität stellt eine Art effektive Konzentration dar, die die Effekte der Nichtidealität der betreffenden Phase beinhaltet.
Die Aktivität wird bei der Berechnung von Reaktionsgeschwindigkeiten und Energiegrößen einer chemischen Reaktion angewendet (siehe chemisches Potential).
Inhaltsverzeichnis
Definition
In einer idealen Mischung ergibt sich das chemisches Potential der Komponenten aus der Gleichung
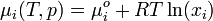 .
.
Für eine reale Mischung muss eine Korrektur vorgenommen werden:
Man sieht, dass die Aktivität dimensionslos sein muss, da eine zu logarithmierende physikalische Größe immer dimensionslos ist. Die Aktivität selbst ist eine Funktion der Stoffmenge und einem unbekannten Faktor:
-
- ai = γi xi
Dieser Faktor wird als Aktivitätskoeffizient bezeichnet. Er ist dimensionlos. Während in einer idealen Mischung keinerlei intermolekulare Wechselwirkungen vorhanden sind und somit die chemischen Potentiale und alle damit verbundenen Größen auf die Stoffmengenanteile der Komponenten zurückzuführen sind, sind in einer realen Mischung Wechselwirkung zwischen den Teilchen vorhanden. Diese Wechselwirkungen können z.B. elektrostatisch sein. Der Aktivitätskoeffizient beschreibt genau diese Abweichungen der Mischung vom Idealverhalten. Er wurde Gilbert Newton Lewis 1907 als rein empirische Größe für starke Elektrolyte eingeführt. Physikalisch untermauert wurde dessen Theorie erst durch Berechnungen von Debye und Hückel.
Aktivität und Aktivitätskoeffizient sind oftmals nur schwer theoretisch bestimmbar. Aus diesem Grund gibt es eine Reihe von Näherungen, mit deren Hilfe man unter bestimmten Umständen wiederum sehr leicht Zugang zu Aktivität findet. Eine Herangehensweise ist, dass man sehr kleine Stoffmengen wählt. Dies führt (natürlich nur in der Theorie) zu folgenden Überlegungen/Ergebnissen:
- wenige Teilchen bedeutet einen großen Abstand der Teilchen und somit keine Wechselwirkungen
- es können Wechselwirkungen mit den Gefäßwänden vernachlässigt werden
Bei Lösungen wird noch angenommen, dass keinerlei nennenswerte Wechselwirkung zwischen Lösemittel und gelöstem Stoff vorhanden sind. Mathematisch lassen sich die Näherungen wie folgt ausdrücken:
-
- ai = xi (allgemein)
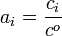 (in Lösungen)
(in Lösungen)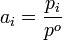 (in Gasgemischen)
(in Gasgemischen)
Die Näherung für Lösungen ist bei Konzentration im Bereich von ca.
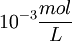 relativ gut (es kommt natürlich auch auf die verwendete Messmethode an). Der Divisor folgt aus der Dimension des chemischen Potentials: Soll a dimensionslos sein, muss man die entsprechende Konzentration durch irgendeine Konzentration teilen. Per definitionem wird die Standardkonzentration co verwendet. Um nun wieder den Schritt zu realen Mischungen zu gehen, werden die benötigten Terme einfach mit dem Aktivitätskoeffizienten multipliziert.
relativ gut (es kommt natürlich auch auf die verwendete Messmethode an). Der Divisor folgt aus der Dimension des chemischen Potentials: Soll a dimensionslos sein, muss man die entsprechende Konzentration durch irgendeine Konzentration teilen. Per definitionem wird die Standardkonzentration co verwendet. Um nun wieder den Schritt zu realen Mischungen zu gehen, werden die benötigten Terme einfach mit dem Aktivitätskoeffizienten multipliziert.Aktivitätskoeffizient
Ingenieurbereich
Im technischen Bereich werden für die Abschätzung des Aktivitätskoeffizienten unter anderem NRTL (Non-Random-Two-Liquid), UNIQUAC (Universal Quasichemical) und UNIFAC (Universal Quasichemical Functional Group Activity Coefficients) eingesetzt.
Elektrochemie
Nach der Interpretation von Debye und Hückel ist
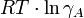 die elektrostatische potentielle Energie, die entsteht, wenn 1 Mol der Ionensorte A vom fiktiven ungeladenen Zustand auf seine reale Ladungsmenge innerhalb seiner entgegengesetzt geladenen Ionenwolke aufgeladen wird. Diese potentielle Energie ist somit negativ („Man muss Energie hineinstecken, um die Ionensorte A aus seiner Ionenwolke zu entfernen“).
die elektrostatische potentielle Energie, die entsteht, wenn 1 Mol der Ionensorte A vom fiktiven ungeladenen Zustand auf seine reale Ladungsmenge innerhalb seiner entgegengesetzt geladenen Ionenwolke aufgeladen wird. Diese potentielle Energie ist somit negativ („Man muss Energie hineinstecken, um die Ionensorte A aus seiner Ionenwolke zu entfernen“).Debye-Hückel:
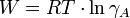
Darin ist R die universelle Gaskonstante und T die Temperatur. W ist negativ; somit liegt γ zwischen 0 und 1. Die Theorie von Debye-Hückel verlangt eine starke Verdünnung von A.
Experimentelle Messungen ergaben eine Abhängigkeit zwischen der Ionenkonzentration von A und seinem Aktivitätskoeffizienten. Für große Konzentrationen von A wird γ größer als eins („Ich gewinne Energie, wenn ich A entferne“). Große Ionenkonzentrationen von A werden von der Debye-Hückel-Theorie nicht berücksichtigt.
Beispiel: Für 1-molare Essigsäure ist γ = 0,8 und für 0,1-molare Essigsäure 0,96.
Ein Verfahren zur Abschätzung von Aktivitätskoeffizienten ist die reguläre Lösungstheorie.
Aktivität eines Lösungsmittels
In Lösungen ist die Aktivität aB eines Stoffes B definiert über
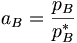
wobei
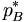 der Dampfdruck des reinen Lösungsmittels ist (der als Standardfugazität gewählt wird), pB der Dampfdruck des Lösungsmittels in der Lösung (eigentlich die Fugazität). a ist in diesem Fall analog zum Molenbruch zu sehen: Dies ist der Molenbruch, der bei Betrachtungen des Systems ausschlaggebend ist. Das Raoultsche Gesetz gilt für Lösungsmittel umso mehr, je näher der Molenbruch sich 1 annähert, d.h. je reiner das Lösungmittel ist. Um das Verhalten anschaulich zu beschreiben, wurde hier ebenfalls ein Korrekturfaktor eingeführt, der nun aB wie folgt definiert:
der Dampfdruck des reinen Lösungsmittels ist (der als Standardfugazität gewählt wird), pB der Dampfdruck des Lösungsmittels in der Lösung (eigentlich die Fugazität). a ist in diesem Fall analog zum Molenbruch zu sehen: Dies ist der Molenbruch, der bei Betrachtungen des Systems ausschlaggebend ist. Das Raoultsche Gesetz gilt für Lösungsmittel umso mehr, je näher der Molenbruch sich 1 annähert, d.h. je reiner das Lösungmittel ist. Um das Verhalten anschaulich zu beschreiben, wurde hier ebenfalls ein Korrekturfaktor eingeführt, der nun aB wie folgt definiert:aB = γBxB mit
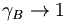 für
für 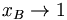
Dieser Zusammenhang lässt sich aus dem chemischen Potential und dem Raoultschen Gesetz ableiten.
Grenzaktivitätskoeffizient
Der Grenzaktivitätskoeffizient
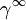 ist der Aktivitätskoeffizient einer Komponente bei unendlicher Verdünnung (
ist der Aktivitätskoeffizient einer Komponente bei unendlicher Verdünnung (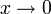 ) in einem Lösungsmittel oder einem Lösungsmittelgemisch.
) in einem Lösungsmittel oder einem Lösungsmittelgemisch.Aktivität von Ionen und Elektrolyten
Für verdünnte Elektrolyte lässt sich der Aktivitätskoeffizient aus der Debye-Hückel-Theorie berechnen. Dabei ist zu beachten, dass die oben angegebene Definitionsgleichung nur für jede individuelle Ionensorte i gilt
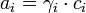
Da aber jede Lösung elektroneutral sein muss, das heißt gleich viele positive wie negative Ladungen aufweisen muss, können individuelle Aktivitäten zwar nutzbringend berechnet, aber nicht gemessen werden. Für einen nach der Gleichung
ν stöchiometrische Koeffizienten z Ladungszahlen (negativ für Anionen) vollständig dissoziierenden Elektrolyten gilt, wenn wir die Indices + für die Kationen
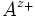 und - für die Anionen
und - für die Anionen 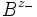 verwenden,
verwenden,Zur Vereinfachung werden
die mittlere Aktivität
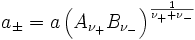
und der mittlere Aktivitätskoeffizient
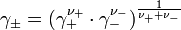
definiert.
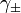 ist z. B. in galvanischen Zellen messbar. Für die mittlere Aktivität des Elektrolyten gilt dann
ist z. B. in galvanischen Zellen messbar. Für die mittlere Aktivität des Elektrolyten gilt dann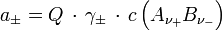
- Darin ist
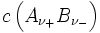 die Konzentration des Elektrolyten.
die Konzentration des Elektrolyten.
Beispiele:
- Für eine wässrige Lösung, die je 10−3 mol · dm–3 Kaliumchlorid (KCl) und Natriumsulfat (Na2SO4) enthält, wird aus dem Debye-Hückel-Grenzgesetz
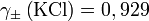 berechnet. Es ist Q = 1, also
berechnet. Es ist Q = 1, also
- Für 0,1-molare Magnesiumchlorid-Lösung (MgCl2) ist
-
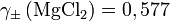 . Mit
. Mit ![Q=\left(1^1\cdot 2^2\right)^\frac{1}{1+2}=\sqrt[3]{4}](/pictures/dewiki/53/5eca8d5dceb109c24857e70e679f8630.png) ergibt sich
ergibt sich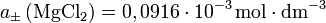 .
.
Siehe auch
Wikimedia Foundation.