- Cramer-Rao-Schranke
-
Die Cramér-Rao-Ungleichung, benannt nach den beiden Mathematikern Harald Cramér und Calyampudi Radhakrishna Rao, liefert in der mathematischen Statistik eine obere Schranke für die Genauigkeit bzw. eine untere Schranke für die Varianz eines Schätzers für einen unbekannten Parameter
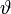 aus dem Parameterraum
aus dem Parameterraum 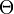 .
.Inhaltsverzeichnis
Definition
Formal gilt für eine Zufallsvariable
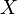 mit unbekannter Dichte
mit unbekannter Dichte 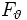 und jeden Schätzer
und jeden Schätzer 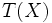 für
für 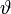 die Ungleichung
die Ungleichung![\mathrm{Var}_{\vartheta}(T(X)) \geq \frac{(\frac{\partial}{\partial \vartheta} \mathrm{E}_{\vartheta}[T(X)])^2}{I(\vartheta)}](/pictures/dewiki/49/15f774ad0bd4336054ca186c52e71d86.png) ,
,sofern die Familie der Wahrscheinlichkeitsdichten bestimmte Regularitätsbedingungen erfüllt:
- Der Träger der Wahrscheinlichkeitsdichten darf nicht vom unbekannten Parameter
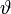 abhängen
abhängen - Die Wahrscheinlichkeitsdichten müssen stetig nach
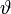 differenzierbar sein
differenzierbar sein ![\mathrm{E}_{\vartheta} \left[T(X)^2 \right]<\infty](/pictures/dewiki/50/29b7cf58b754a0a0af2003138d981ec8.png)
- Es muss folgende Vertauschungsrelation gelten:
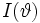 bezeichnet die Fisher-Information.
bezeichnet die Fisher-Information.Effizienz und Optimalität
Wenn für einen Schätzer
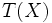 die Identität
die Identität![\mathrm{Var}_{\vartheta}(T(X)) = \frac{(\frac{\partial}{\partial \vartheta} E_{\vartheta}[T(X)])^2}{I(\vartheta)}](/pictures/dewiki/55/7d5a6255705202fe5b5e59f2cc72cb18.png)
gilt, so heißt er effizient. Wenn er zudem erwartungstreu ist, so ist er bezüglich der mittleren quadratischen Abweichung optimal. Für einen erwartungstreuen Schätzer vereinfacht sich die untere Schranke zur inversen Fisher-Information.
Regularitätsbedingungen und Beweisidee
Der Beweis der Cramér-Rao-Ungleichung beruht im wesentlichen auf der Cauchy-Schwarz-Ungleichung und zwei Modellannahmen, die die Vertauschbarkeit von Differentiation und Integration regeln.
Einerseits soll
gelten und andererseits nehmen wir
an. Direktes Einsetzen in die Cauchy-Schwarz-Ungleichung liefert dann die Behauptung.
Mehrdimensionale Formulierung
Unter ähnlichen Regularitätsbedingungen ist die Cramér-Rao-Ungleichung auch im Falle mehrdimensionaler Parameter formulierbar. Die Aussage überträgt sich dann auf die Betrachtung der Kovarianzmatrix des mehrdimensionalen Schätzers und liefert eine
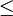 -Relation im Sinne der Löwner-Ordnung für Matrizen.
-Relation im Sinne der Löwner-Ordnung für Matrizen. - Der Träger der Wahrscheinlichkeitsdichten darf nicht vom unbekannten Parameter
Wikimedia Foundation.

![\mathrm\frac{\partial}{\partial\vartheta}{E}_{\vartheta}\left[T(X) \right]=\frac{\partial}{\partial\vartheta}\int (T \cdot F_{\vartheta})(x) \;\mu \,(dx) =\int \frac{\partial}{\partial\vartheta}(T \cdot F_{\vartheta})(x) \;\mu \,(dx)](/pictures/dewiki/102/fba5c6310c866675d4e590102374348b.png)
![\mathrm{E}_{\vartheta}
\left[
\frac{\partial}{\partial\vartheta} \log f_{\vartheta}(X_i)
\right]
= 0](/pictures/dewiki/56/8219ecde00fa9abb12c5f45c611760c2.png)
![\mathrm{E}_{\vartheta}
\left[
T(X) \frac{\partial}{\partial\vartheta} \log f_{\vartheta}(X_i)
\right]
=
\frac{\partial}{\partial\vartheta} \mathrm{E}_{\vartheta}
\left[
T(X)
\right]](/pictures/dewiki/56/844362399b3a2470e7eddae631e6fb8f.png)