- Deckungsgleichheit
-
In der Geometrie sind zwei Flächen kongruent (deckungsgleich) (von lat. congruens = übereinstimmend, passend), wenn sie durch eine Kongruenzabbildung ineinander überführt, d.h. zur Deckung gebracht werden können. Kongruenzabbildungen (auch Bewegungen genannt) sind Parallelverschiebung, Drehung, Spiegelung und die Verknüpfungen dieser Abbildungen.
Die Kongruenz ebener geometrischer Figuren lässt sich anschaulich so deuten: Man kann die eine Figur mit der Schere ausschneiden und so auf die andere legen, dass beide genau übereinander liegen. Das Gegenteil der Kongruenz ist die Inkongruenz.
Kongruente Figuren zeichnen sich dadurch aus, dass entsprechende Streckenlängen und Winkelgrößen übereinstimmen.
Inhaltsverzeichnis
Beispiel
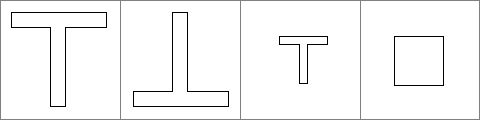
Die ersten beiden Figuren sind kongruent. Die dritte hat zwar dieselbe Form, ist aber kleiner. Sie ist daher ähnlich zu der ersten und zweiten Figur, aber nicht kongruent. Die letzte Figur ist zwar gleich groß wie die dritte, hat aber nicht dieselbe Form und ist somit nicht kongruent.
Kongruenz von Dreiecken
Besonders leicht lässt sich die Kongruenz von Dreiecken überprüfen. Die vier Kongruenzsätze SSS, WSW, SWS und SSW (W = Winkel, S = Seite) liefern einfache Bedingungen, unter denen zwei Dreiecke kongruent sind.
Punktgruppe (Symmetriegruppe) einer Figur
Die Menge aller Kongruenzabbildungen (Kongruenzen) einer Figur bildet deren Punktgruppe oder auch Symmetriegruppe. Im obigen Beispiel besteht diese aus der Identität und einer Spiegelung. Im Fall des regulären n-Ecks besteht diese aus n Drehungen (einschl. der Identität) und n Spiegelungen.
Kongruenz in der Raumgeometrie
In der Stereometrie (Raum-Geometrie) spricht man bei Polyedern gegebenenfalls auch von der Kongruenz von Ecken, falls zwei Ecken dieselbe Anzahl von Kanten und Flächen mit denselben Winkeln (in derselben Reihenfolge) vereinigen; dabei müssen nicht nur die Winkel in den Seitenflächen des Polyeders gleich sein, sondern auch alle Winkel zwischen entsprechenden Kantenpaaren. Die eine Ecke muss sich ggf. durch eine Kongruenzabbildung in die andere überführen lassen, dies ist die wesentliche Eigenschaft.
Wikimedia Foundation.