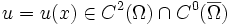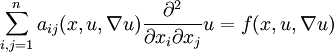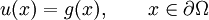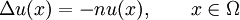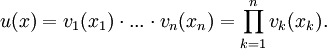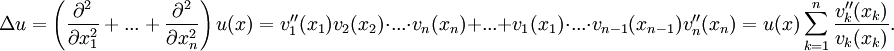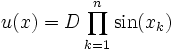Dirichlet-Rand

Als Dirichlet-Randbedingung (nach Peter Gustav Lejeune Dirichlet) bezeichnet man im Zusammenhang mit Differentialgleichungen (genauer: Randwertproblemen), Werte, die auf dem jeweiligen Rand des Definitionsbereichs von der Funktion angenommen werden sollen. Weitere Randbedingungen sind beispielsweise Neumann-Randbedingungen oder schiefe Randbedingungen.

Gewöhnliche Differentialgleichung

Das Dirichletproblem

Im Falle einer gewöhnlichen Differentialgleichung ist der Definitionsbereich der Funktion ein abgeschlossenes Intervall. Folglich besteht der Rand des Definitionsbereiches nur aus dem rechten und dem linken Intervall-Ende. Aufgrund der Freiheit in gewöhnlichen Differentialgleichungen sind Dirichlet-Randbedingungen nur für Gleichungen von zweiter oder höherer Ordnung sinnvoll. In diesem Fall sieht ein Dirichletproblem, d.h. eine Differentialgleichung mit Dirichlet-Randbedingung folgendermaßen aus:

$y \in C^2(a,b)\cap C^0[a,b]$

y'' = f(x,y,y')

$y(a) = \alpha,\quad y(b) = \beta$

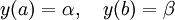
Hierbei ist die rechte Seite f der Differentialgleichung eine vorgeschriebene Funktion, α und β sind vorgeschriebene reelle Zahlen für die Funktionswerte einer Lösung an den Intervallenden. Schließlich suchen wir eine Lösung y aus der angegebenen Regularitätsklasse.

Beispiel für eine gewöhnliche Differentialgleichung

Wir wählen als unser Intervall [0,π] und betrachten das folgende Dirichletproblem:

$y \in C^2(0,\pi)\cap C^0[0,\pi]$

y'' = − y

$y(0) = 0,\quad y(\pi) = 0$

Mit der Theorie der linearen gewöhnlichen Differentialgleichungen mit konstanten Koeffizienten erhalten wir zunächst als allgemeine Lösung der Differentialgleichung:

y(x) = Ccosx + Dsinx

mit zwei frei wählbaren reellen Konstanten C und D. Wir benutzen die Randbedingungen, um diese Konstanten zu fixieren. Dabei erhalten wir ein lineares Gleichungssystem in den Unbekannten C und D:

C = 0,

− C = 0.

Bemerkenswerter Weise ist dieses System nicht eindeutig lösbar, aber es ist für beliebiges reelles D eine Lösung gegeben durch

y(x) = Dsinx.

Partielle Differentialgleichungen

Das Dirichletproblem

Bei einer partiellen Differentialgleichung ist die alleinige Angabe von Neumann-Randbedingungen nur für elliptische Gleichungen auf einem beschränkten Gebiet 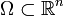$\Omega\subset\R^n$ sinnvoll, da die anderen Typen auch Vorgaben der Anfangswerte benötigen. Dabei werden Dirichlet-Randbedingungen auf dem Rand des Gebietes 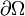$\partial\Omega$ vorgeschrieben. Wir definieren hier das Dirichletproblem für eine quasilineare partielle Differentialgleichung:

$u=u(x)\in C^2(\Omega)\cap C^0(\overline\Omega)$

$\sum_{i,j=1}^n a_{ij}(x,u,\nabla u)\frac{\partial^2}{\partial x_i\partial x_j} u = f(x,u,\nabla u)$

$u(x) = g(x),\qquad x\in\partial\Omega$

Hierbei stellt die Funktion 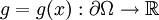$g=g(x):\partial\Omega\rightarrow\R$ die vorgeschriebenen Funktionswerte unserer Lösung dar. Allein die Frage nach der Lösbarkeit eines solchen Problemes ist schon sehr anspruchsvoll und steht im Mittelpunkt der aktuellen Forschung. Es ist auch sehr schwierig, eine allgemeingültige Lösungsmethode anzugeben.

Beispiel für eine partielle Differentialgleichung

Wir betrachten in diesem Beispiel auf dem Gebiet 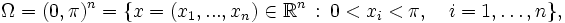$\Omega = (0,\pi)^n = \{x=(x_1,...,x_n)\in\R^n\,:\, 0< x_i< \pi, \quad i=1,\dots,n\},$ das folgende Randwertproblem:

$u=u(x)\in C^2(\Omega)\cap C^0(\overline \Omega)$

$\Delta u(x) = -nu(x),\qquad x\in \Omega$

$u(x) = 0,\qquad x\in\partial \Omega.$

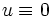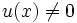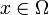Hierbei bezeichnet Δ den Laplace-Operator. Zunächst stellen wir fest, dass $u\equiv 0$ eine Lösung des Problems ist. Wir wollen noch weitere Lösungen finden. Wir nehmen nun $u(x)\neq 0$ für $x\in\Omega$ an und machen den folgenden Produktansatz

$u(x) = v_1(x_1)\cdot ...\cdot v_n(x_n) = \prod_{k=1}^n v_k(x_k).$

Für die Funktionen v_k leiten wir gewöhnliche Differentialgleichungen mit entsprechenden Dirichlet-Randbedingungen her. Es folgt

$\Delta u = \left (\frac{\partial^2}{\partial x_1^2}+...+\frac{\partial^2}{\partial x_n^2}\right )u(x) = v_1''(x_1)v_2(x_2)\cdot...\cdot v_n(x_n) + ... + v_1(x_1)\cdot ...\cdot v_{n-1}(x_{n-1})v_n''(x_n) = u(x) \sum_{k=1}^n \frac{v_k''(x_k)}{v_k(x_k)}.$

Wenn nun die v_k dem Randwertproblem

$v_k \in C^2(0,\pi)\cap C^0[0,\pi]$

v_k'' = − v_k

$v_k(0) = 0,\quad v_k(\pi) = 0$

genügen, dann ist die oben definierte Funktion u eine Lösung des Dirichlet-Randwertproblems für die partielle Differentialgleichung. Mit dem Beispiel für gewöhnliche Differentialgleichungen erhalten wir

v_k(x) = D_ksin(x_k)

und somit

$u(x) = D\prod_{k=1}^n\sin(x_k)$

als Lösung unseres Problems partieller Differentialgleichungen zu Dirichlet-Randbedingungen. Offen bleibt die Frage, ob es noch weitere Lösungen gibt.

Literatur

• D. Gilbarg, N.S. Trudinger: Partial Differential Equations of Second Order, Springer-Verlag, Berlin 1998, ISBN 3-540-41160-7.