- Drehhyperboloid
-
Das Rotationshyperboloid ist eine Fläche zweiter Ordnung, die man sich durch Rotation einer Geraden um eine zu ihr windschiefe Gerade (Achse) entstanden vorstellen kann. Das Rotationshyperboloid ist ein Spezialfall des einschaligen Hyperboloids. Seine gaußsche Krümmung ist in jedem Punkt negativ; es handelt sich also um eine antiklastisch gekrümmte Fläche.
Die Oberflächen der meisten Kühltürme sind Rotationshyperboloide.
Die Gleichung ergibt sich aus der allgemeinen Gleichung eines einschaligen Hyperboloids
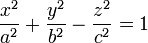
durch Einsetzen von
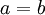 .
.Die Gerade mit der Parametergleichung
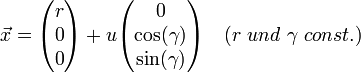
erzeugt bei Rotation um die z-Achse das Rotationshyperboloid
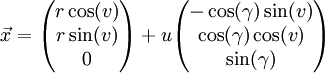 .
.
Wikimedia Foundation.

