Endliche und unendliche Mengen

In der Mengenlehre, einem Teilgebiet der Mathematik, definiert man:

• Eine Menge M heißt endlich, wenn es eine natürliche Zahl n gibt, sodass M genau n Elemente hat. Das heißt also, dass M entweder leer ist (das ist der Fall n = 0), oder dass es eine Bijektion von M auf die Menge {1,...,n} gibt.
• Eine Menge M heißt unendlich, wenn es keine solche natürliche Zahl gibt.

Im Gegensatz zur Unendlichkeitsdefinition von Dedekind erlaubt es diese Definition, Aussagen der Form "alle endlichen Mengen haben die Eigenschaft X" mit Hilfe der vollständigen Induktion zu beweisen. Man muss also zeigen, dass erstens die leere Menge die Eigenschaft X hat, und dass zweitens für jede endliche Menge M gilt: wenn M die Eigenschaft X hat, und a ein beliebiges Objekt außerhalb von M ist, dann hat auch 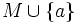$M \cup \{a\}$ die Eigenschaft X.

Um zum Beispiel zu zeigen, dass jede endliche Menge auch Dedekind-endlich ist, genügt es, folgendes zu zeigen

1. Die leere Menge ist zu keiner echten Teilmenge gleichmächtig.
2. Wenn M zu keiner echten Teilmenge gleichmächtig ist, dann ist auch 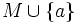$M \cup \{a\}$ zu keiner echten Teilmenge (von sich selbst) gleichmächtig.

(Punkt 1 ist sehr leicht; um Punkt 2 zu zeigen, muss man zeigen, wie man aus einer Bijektion f' zwischen der Menge M' := 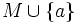$M \cup \{a\}$ und einer echten Teilmenge U' von M' eine Bijektion f zwischen M und einer echten Teilmenge U gewinnen kann.)

Mächtigkeit

Der mengentheoretische Begriff des Unendlichen wird noch interessanter, da es verschiedene Mengen gibt, die unendlich viele Elemente besitzen, die aber nicht bijektiv aufeinander abgebildet werden können. Diese unterschiedlichen Mächtigkeiten werden mit dem Symbol ℵ (Aleph, dem ersten Buchstaben des hebräischen Alphabets), und einem (anfangs ganzzahligen) Index bezeichnet (die Indizes durchlaufen die Ordinalzahlen).

Die Mächtigkeit der natürlichen Zahlen (die kleinste Unendlichkeit) ist in dieser Schreibweise ℵ₀.

Die Reellen Zahlen bilden eine unendliche Menge, die mächtiger als die Menge der natürlichen Zahlen ist, sie ist überabzählbar.

Die Kontinuumshypothese ist die Behauptung, dass die Mächtigkeit der reellen Zahlen gleich ℵ₁, also die nach ℵ₀ nächstgrößere Mächtigkeit, ist. Sie ist allein mit den üblichen Axiomen der Mengenlehre (ZFC) weder beweisbar noch widerlegbar.

Zu jeder unendlichen Menge lassen sich weitere Unendlichkeiten mittels Bildung der Potenzmenge (Menge aller Teilmengen) konstruieren. Ob hierbei aus einer Menge mit Mächtigkeit ℵ_n eine Menge der nächstgrößeren Mächtigkeit ℵ_n+1 entsteht oder einige Größenordnungen übersprungen werden, ist ein klassisches Problem der Mengenlehre (die verallgemeinerte Kontinuumshypothese). Dieser Vorgang kann (formal) immer weiter geführt werden, so dass es unendlich viele Unendlichkeiten gibt (ein wahrlich die Anschauung strapazierendes Konzept).

Es gibt in der Mengenlehre mehrere „Zahlensysteme“, die unendlich große Zahlen enthalten. Die bekanntesten sind Ordinalzahlen, Kardinalzahlen, Hyperreelle Zahlen und Surreale Zahlen.

Siehe auch

• Unendlichkeit