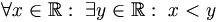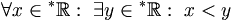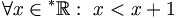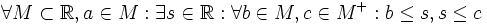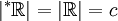- Hyperreelle Zahlen
-
In der Mathematik sind Hyperreelle Zahlen ein Untersuchungsgegenstand der Nichtstandardanalysis. Die Menge der hyperreellen Zahlen wird meist als
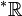 geschrieben; sie erweitert die reellen Zahlen um ihre infinitesimal benachbarten Zahlen sowie um unendlich große (infinite) Zahlen.
geschrieben; sie erweitert die reellen Zahlen um ihre infinitesimal benachbarten Zahlen sowie um unendlich große (infinite) Zahlen.Als Newton und Leibniz ihre Differentialrechnung mit „Fluxionen“ durchführten, benutzten sie infinitesimale Zahlen, und noch Euler und Cauchy fanden sie nützlich. Trotzdem wurden diese Zahlen von Anfang an skeptisch betrachtet, und im 19. Jahrhundert wurde die Analysis durch die Einführung der epsilon-delta-Definition des Grenzwertes durch Cauchy, Weierstraß und andere auf eine solide Grundlage gestellt. Infinitesimale Zahlen wurden von da an nicht mehr benutzt.
Abraham Robinson (1918-1974) zeigte dann in den 1960ern, auf welche Weise unendlich große und kleine Zahlen streng formal definiert werden können und eröffnete so das Gebiet der Nichtstandard-Analysis. Da Robinsons Theorie in ihrer strengsten Form umfassenden Gebrauch von der klassischen Logik und der Mengenlehre, insbesondere vom Auswahlaxiom, macht, wird sie als nichtkonstruktiv angesehen. Die hier gegebene Konstruktion ist eine (immer noch nichtkonstruktive) vereinfachte Version, die zuerst von Lindstrom gegeben wurde.
Durch die hyperreellen Zahlen ist eine Formulierung der Differential- und Integralrechnung ohne den Grenzwertbegriff möglich.
Eine weitere Klasse von Nichtstandard-Zahlen ist die echte Klasse der surrealen Zahlen, die nicht nur die reellen, sondern auch die hyperreellen Zahlen und alle Ordinalzahlen enthält.
Inhaltsverzeichnis
Eigenschaften
Die hyperreellen Zahlen
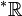 bilden einen geordneten Körper, der
bilden einen geordneten Körper, der  als Teilkörper enthält. Im Gegensatz zu den reellen Zahlen bilden die hyperreellen Zahlen keinen metrischen Raum, doch aufgrund ihrer Ordnung tragen sie eine Ordnungstopologie.
als Teilkörper enthält. Im Gegensatz zu den reellen Zahlen bilden die hyperreellen Zahlen keinen metrischen Raum, doch aufgrund ihrer Ordnung tragen sie eine Ordnungstopologie.Eine logische Aussage der Prädikatenlogik erster Stufe heißt im Kontext der Nichtstandard-Analysis wohlgeformt, wenn sie nur bestimmte grundlegende Verknüpfungen (Grundrechenarten, Vergleich) und natürliche Zahlen enthält und nur über reelle Zahlen quantifiziert (siehe Allquantor, Existenzquantor; insbesondere darf sie nicht über Elemente einer echten Teilmenge von
 ' oder über Mengen von reellen Zahlen quantifizieren).
' oder über Mengen von reellen Zahlen quantifizieren).Die hyperreellen Zahlen sind auf eine solche Weise definiert, dass jede wohlgeformte Aussage auch zutrifft, wenn man sie über hyperreelle Zahlen quantifiziert. Zum Beispiel können wir sagen, dass für jede reelle Zahl eine größere Zahl existiert:
Dieselbe Aussage trifft dann auch für hyperreelle Zahlen zu:
Ebenso kann man aussagen, dass man eine größere Zahl erhält, wenn man 1 zu einer reellen Zahl addiert:
Dasselbe gilt für hyperreelle Zahlen:
Das heißt nun nicht, dass
 und
und 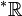 sich genau gleich verhalten. Zum Beispiel gibt es in
sich genau gleich verhalten. Zum Beispiel gibt es in 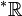 ein Element w mit der folgenden Eigenschaft:
ein Element w mit der folgenden Eigenschaft:- 1 < w, 1+1 < w, 1+1+1 < w, 1+1+1+1 < w, ...
Eine solche Zahl gibt es in
 nicht. Eine hyperreelle Zahl wie w nennt man infinit, der Kehrwert einer unendlich großen Zahl ist eine infinitesimale Zahl.
nicht. Eine hyperreelle Zahl wie w nennt man infinit, der Kehrwert einer unendlich großen Zahl ist eine infinitesimale Zahl.Eine weitere Eigenschaft der reellen Zahlen, die sich nicht auf die hyperreellen überträgt, ist die Dedekind-Vollständigkeit: Jede nichtleere nach oben beschränkte Teilmenge von
 hat eine obere Grenze. Diese Forderung charakterisiert die Menge der reellen Zahlen eindeutig: Jeder Dedekind-vollständige Körper ist isomorph zu
hat eine obere Grenze. Diese Forderung charakterisiert die Menge der reellen Zahlen eindeutig: Jeder Dedekind-vollständige Körper ist isomorph zu  .
.Für die reelle Teilmenge M sei
 . Dann lässt sich die Dedekind-Vollständigkeit so formalisieren:
. Dann lässt sich die Dedekind-Vollständigkeit so formalisieren:Diese Aussage ist nicht auf hyperreelle Zahlen übertragbar, weil sie nicht nur über reelle Zahlen, sondern auch über Mengen reeller Zahlen quantifiziert (M ⊆
 ).
).Die hyperreellen Zahlen sind gleichmächtig zu den reellen Zahlen.
Konstruktion
Wir konstruieren die hyperreellen Zahlen als Folgen reeller Zahlen. Wir wollen
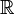 durch die Identifikation einer reellen Zahl r mit der konstanten Folge (r, r, r, ...) in die so konstruierten Zahlen einbetten. Zum Beispiel haben wir
durch die Identifikation einer reellen Zahl r mit der konstanten Folge (r, r, r, ...) in die so konstruierten Zahlen einbetten. Zum Beispiel haben wir- 0 = (0,0,0,0,...),
- 1 = (1,1,1,1,...),
- π = (π,π,π,π,...).
Die Rechenoperationen definieren wir gliedweise:
- (a0,a1,a2,...) + (b0,b1,b2,...) = (a0 + b0,a1 + b1,a2 + b2,...)
Analog definieren wir die Multiplikation.
zum Beispiel ist dann
- 1 + 3 = (1,1,1,1,...) + (3,3,3,3,...) = (1 + 3,1 + 3,1 + 3,1 + 3,...) = (4,4,4,4,...) = 4.
Für jede Folge a = (a0,a1,a2,...) gilt dann z. B.
 .
.
Formal gesehen haben wir bislang das abzählbar unendliche direkte Produkt
 des Körpers
des Körpers  mit der komponentenweisen Addition und Multiplikation gebildet. Dieses
mit der komponentenweisen Addition und Multiplikation gebildet. Dieses 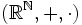 ist allerdings kein Körper, sondern lediglich ein kommutativer unitärer Ring. Zum Beispiel existiert zu jeder Folge, die auch nur an einer Stelle eine 0 aufweist, keine multiplikative Inverse.
ist allerdings kein Körper, sondern lediglich ein kommutativer unitärer Ring. Zum Beispiel existiert zu jeder Folge, die auch nur an einer Stelle eine 0 aufweist, keine multiplikative Inverse.Für das weitere Vorgehen ist folgende Zielrichtung maßgeblich: Den „Wert“ einer als Folge konstruierten Zahl wollen wir am Verhalten im Unendlichen ablesen, d. h. insbesondere die ersten endlich vielen Folgenglieder sollen für die Wertigkeit der Zahl keine Rolle spielen.
Wir möchten nun die konstruierten Folgen vergleichen, geraten aber schnell in Schwierigkeiten: Einige Einträge der ersten Folge könnten größer, andere könnten kleiner sein als die entsprechenden Einträge der zweiten Folge. Wir müssen angeben, welche Positionen „eine Rolle spielen“.
Betrachten wir z. B. die Folgen
- a = (1;0,1;0,01;0,001;0,0001;...)
- b = (0;2;0,01;0,001;0,0001;...)
- c = (0;1;1;1;1;...)
- d = (1;0;1;1;1;...)
Die Folgen a und b unterscheiden sich nur an den ersten zwei Einträgen, ebenso die Folgen c und d. Es ist daher sinnvoll, a und b gleichzusetzen, und c und d gleichzusetzen. Vergleichen wir a und c: Jede Komponente von a - außer der ersten - ist kleiner als die entsprechende Komponente von c. Die Folge a sollte also kleiner sein als c. Allgemein spielt es keine Rolle, wenn zwei Folgen sich nur an endlich vielen Stellen unterscheiden. Ein Problem bekommen wir dann beim Vergleich von alternierenden Folgen wie diesen beiden:
- e = (1;0;1;0;1;0;...)
- f = (0;1;0;1;0;1;...)
Die Folge e ist an unendlich vielen Stellen kleiner als f, aber auch an unendlich vielen Stellen größer als f.
Hier schafft die Theorie Abhilfe, indem wir feststellen: Eine konsistente Angabe, welche Positionen „eine Rolle spielen“, gibt ein freier Ultrafilter U auf den natürlichen Zahlen. Ein solches U existiert nach dem Auswahlaxiom. (Genaugenommen existieren viele freie Ultrafilter, aber man kann zeigen, dass die Wahl des Ultrafilters keine Rolle spielt). Mit Hilfe von U können wir nun eine Ordnungsrelation definieren:
- (a0, a1, a2, ...) ≤ (b0, b1, b2, ...), falls {n : an ≤ bn} in U.
Dies liefert eine totale Präordnung auf der Menge der reellen Zahlenfolgen. Definieren wir noch eine Äquivalenzrelation:
- a = b, falls a ≤ b und b ≤ a.
Auf der Menge der Äquivalenzklassen, die wir mit
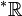 bezeichnen, ist die Ordnungsrelation nun eine totale Ordnung. Addition und Multiplikation der Äquivalenzklassen sind wohldefiniert, und wir haben somit den Körper der hyperreellen Zahlen konstruiert.
bezeichnen, ist die Ordnungsrelation nun eine totale Ordnung. Addition und Multiplikation der Äquivalenzklassen sind wohldefiniert, und wir haben somit den Körper der hyperreellen Zahlen konstruiert.Je nach Wahl des Ultrafilters erhalten wir 0 = e < f = 1 oder 1 = e > f = 0 als Anordnung von e und f (je nachdem, ob die Menge der geraden Stellen oder die Menge der ungeraden Stellen im Ultrafilter, also „wesentlich“, ist).
Infinitesimale und unendlich große Zahlen
Eine hyperreelle Zahl e heißt infinitesimal, wenn sie kleiner ist als jede positive reelle Zahl, aber größer als jede negative reelle Zahl. Die Zahl Null ist die einzige infinitesimale reelle Zahl, aber es gibt andere hyperreelle infinitesimale Zahlen. Die oben definierte Zahl a ist größer als 0, aber kleiner als jede positive reelle Zahl (denn der Ultrafilter enthält alle Komplemente endlicher Mengen).
Eine hyperreelle Zahl x heißt endlich, wenn es eine natürliche Zahl n gibt mit -n < x < n, anderenfalls heißt x unendlich. Die Zahl A = (1;10;100;1000;...) ist eine infinite Zahl. Beachte: Die Bezeichnung „unendlich groß“ bezeichnet meist eine Zahl, die größer ist als jede natürliche Zahl, "unendlich" schließt aber auch Zahlen ein, die kleiner sind als jede ganze Zahl, wie − A = ( − 1; − 10; − 100;...).
Eine von 0 verschiedene Zahl x ist genau dann unendlich, wenn 1/x infinitesimal ist. Zum Beispiel ist
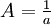 .
.Es lässt sich zeigen, dass jede endliche hyperreelle Zahl „sehr nah“ an genau einer reellen Zahl liegt. Genauer: Ist x eine endliche hyperreelle Zahl, dann gibt es genau eine reelle Zahl st(x), so dass x − st(x) infinitesimal ist. Die Zahl st(x) nennt man den Standardteil' von x, die Differenz zu x ist der Nichtstandardteil. Die Abbildung st hat einige angenehme Eigenschaften: Für alle endlichen hyperreellen Zahlen x, y gilt:
- st(x + y) = st(x) + st(y),
- st(xy) = st(x)st(y),
- st(x) = x genau dann, wenn x reell ist,
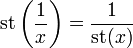 , falls x endlich und nicht infinitesimal ist,
, falls x endlich und nicht infinitesimal ist,- die Abbildung st ist stetig bzgl. der Ordnungstopologie auf der Menge der endlichen hyperreellen Zahlen.
Die ersten zwei Eigenschaften (und die Folgerung st(0) = 0,st(1) = 1 aus der dritten Eigenschaft) besagen, dass st ein Ring-Homomorphismus ist.
Zum Beispiel ist die hyperreelle Zahl g = (0;0,9;0,99;0,999;...) gliedweise kleiner als ( 1; 1; 1; 1; ...), also ist g < 1. Sie ist aber größer als jede reelle Zahl kleiner 1. Sie ist daher zur 1 infinitesimal benachbart und 1 ist ihr Standardteil. Ihr Nichtstandardteil (die Differenz zu 1) ist
- g − 1 = ( − 1; − 0,1; − 0,01; − 0,001;...) = − a.
Beachte aber, dass die reelle Zahl 0,999... als Grenzwert der Folge g gleich 1 ist.
Weblinks
- Jordi Gutierrez Hermoso: Nonstandard Analysis and the Hyperreals -- Eine englische Einführung.
- Manfred Wolff: Nonstandard-Analysis deutsch
Wikimedia Foundation.