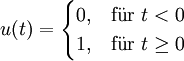Erzwungene Bewegung

Eigenbewegung oder freie Bewegung bezeichnet in der Regelungstechnik die Bewegung, die ein System allein durch seine Ausgangsauslenkung ohne Erregung von Außen ausführt. Durch sie ist eine Aussage über die Stabilität eines Systems möglich.

Aussage über die Stabilität durch die Eigenbewegung

Beispiel für Metastabilität

Bei linearen Systemen gelten die folgenden Aussagen, einmal nachgewiesen, global, da die Systemeigenschaften nicht von den Zuständen x abhängen. Bei nichtlinearen Systemen ist der globale Nachweis dieser Eigenschaften schwieriger, jedoch kann durch sie eine lokale Aussage über die Stabilität gemacht werden.

Ein System

• $\dot x=\mathrm{ax}(\mathrm{t}),\ x(0) = x_0$
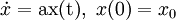
  • a < 0, die Eigenbewegung klingt ab und das System geht bei linearen Systemen asymptotisch in den Ruhestand x = 0 (asymptotisch stabil) über).
  • a = 0, das System verharrt im Ausgangszustand x₀
  • a > 0 klingt die Eigenbewegung auf, das bedeutet bei linearen Systemen ein exponentielles Wachstum über alle Grenzen.

Bei linearen Mehrgrößensystemen in Zustandsraumdarstellung, kann diese Eigenschaft über die Realteile der Eigenwerte r_ei nachgewiesen werden. Dabei gilt:

• Sind alle r_ei < 0 ist das System stabil.
• Sind alle r_ei = 0 ist das System an der Stabilitätsgrenze.
• Ist mindestens ein r_ei > 0 ist das System instabil.

Ein nichtlineares System kann auch meta stabil sein, d.h. das System kann in einem gewissen Bereich stabil sein, dann aber ab einen gewissen Zustand instabil werden oder in einen anderen Ruhepunkt übergehen. Deshalb ist für den Nachweis der global asymptotischen Stabilität bei nichtlinearen Systemen eine komplexere Analyse, Beispielsweise über die Ljapunov-Funktion, notwendig. Bei der Analyse über die Ljapunov-Funktion wird der energetische Zustand eines Systems betrachtet. Nimmt die Energie eines autonomen Systems stetig ab, so muss dies auch für die Zustandsgrößen gelten. Sie beruht also auf einem ähnlichen Grundsatz, siehe dazu auch Stabilitätstheorie.

Erzwungene Bewegung

Bei der erzwungenen Bewegung wird die Reaktion das System auf ein Eingangssignal u(t) überprüft. Typische Eingangssignale sind die Sprungfunktion oder periodische Signale.

Die Reaktion setzt sich dabei additiv aus der freien und der erzwungenen Bewegung zusammen.

Bei der Sprungfunktion gilt:

• $u(t)=\begin{cases} 0, &amp;amp;amp; \text{f}\ddot \text{u}\text{r }t &amp;amp;lt; 0 \\1, &amp;amp;amp; \text{f}\ddot \text{u}\text{r }t\geq 0 \end{cases}$

Für diese Funktion ist ein Tanksystem ohne Ausfluss (Integrales Verhalten) instabil aber zum Beispiel ein Motor stabil, da dieser kein integrales Verhalten besitzt. Es können folgende Fälle unterschieden werden:

• das System nähert sich asymptotisch dem Endwert
• das System wächst über alle Grenzen

Diese Untersuchung ist insbesondere bei meta stabilen Systemen von Bedeutung, also nicht linearen Systemen, da es dann zu größeren Abhängigkeiten von der Eingangsgröße kommen kann.

Zudem wird die erzwungene Bewegung sehr oft zur Charakterisierung von Systemen verwandt.

Siehe auch

Interessant ist hierzu die Eigenfrequenz, dass die Frequenz mit der ein schwingfähiges System nach einmaliger Anregung schwingen kann (bei Vernachlässigung der Dämpfung)

• Zustandsraumdarstellung
• Stabilität
• Polstelle
• Nullstelle

Literatur

• Jan Lunze: Regelungstechnik Bd. 1. Springer Verlag, 2005, ISBN 3-540-28326-9. 
• Jan Lunze: Regelungstechnik Bd. 2. Springer Verlag, 2006, ISBN 3-540-32335-X.