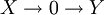Finales Objekt

Anfangsobjekt, Endobjekt und Nullobjekt sind Begriffe aus dem mathematischen Teilgebiet der Kategorientheorie.

Die folgenden Bezeichnungen sind ebenfalls üblich: initiales Objekt für Anfangsobjekt, terminales oder finales Objekt für Endobjekt.

Ein Anfangsobjekt ist ein spezieller Fall des Koprodukts, ein Endobjekt ein spezieller Fall des Produkts in Kategorien.

Definitionen

• Ein Objekt X heißt Anfangsobjekt, wenn Mor(X,Y) für jedes Objekt Y aus genau einem Element besteht, es also einen eindeutigen Morphismus 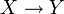$X \to Y$ gibt.
• Ein Objekt X heißt Endobjekt, wenn Mor(Y,X) für jedes Objekt Y aus genau einem Element besteht, es also einen eindeutigen Morphismus 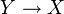$Y \to X$ gibt.

• Ein Objekt heißt Nullobjekt, wenn es gleichzeitig Anfangs- und Endobjekt ist.

Eigenschaften

• Je zwei Anfangsobjekte sind isomorph.
• Je zwei Endobjekte sind isomorph.
• Je zwei Nullobjekte sind isomorph.
• Ist ein Anfangsobjekt zu einem Endobjekt isomorph, dann handelt es sich um ein Nullobjekt.

Die in all diesen Fällen auftretenden Isomorphismen sind jeweils eindeutig bestimmt. Zusammenfassend bedeutet dies:

Anfangs-, End- und Nullobjekte sind (soferne sie existieren) jeweils eindeutig bis auf eindeutigen Isomorphismus.

• Das Anfangsobjekt ist ein Sonderfall des Koprodukts, nämlich für die leere Familie von Objekten.
• Das Endobjekt ist ein Sonderfall des Produkts, nämlich für die leere Familie von Objekten.

Beispiele

• In der Kategorie der Mengen ist die leere Menge das Anfangsobjekt, jede einelementige Menge (Singleton) ist ein Endobjekt.
• In der Kategorie der Gruppen oder der abelschen Gruppen ist die triviale Gruppe (die nur aus dem neutralen Element besteht) Nullobjekt.
• In der Kategorie der nichtleeren Halbgruppen gibt es kein Anfangsobjekt. Lässt man die leere Halbgruppe zu, so ist diese das Anfangsobjekt. In beiden Fällen ist jede einelementige Halbgruppe Endobjekt.
• In der Kategorie der Vektorräume über einem Körper (oder allgemeiner der Moduln über einem Ring) ist der Nullvektorraum (bzw. der Nullmodul) Nullobjekt.
• In der Kategorie der kommutativen Ringe mit Einselement ist der Ring Z der ganzen Zahlen Anfangsobjekt und der Nullring Endobjekt.
• In der Kategorie beliebiger Ringe ist der Nullring Nullobjekt.
• In der Kategorie der punktierten topologischen Räume sind die einpunktigen Räume Nullobjekte.
• Man kann jede partielle Ordnung als Kategorie auffassen indem man festlegt, dass genau dann ein Pfeil von x nach y geht, wenn 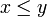$x \le y$ gilt. Ein Anfangsobjekt entspricht dann dem kleinsten Element der Ordnung (falls es existiert). Ein Endobjekt entspricht dem größten Element.

Kategorien mit Nullobjekten

Gibt es in einer Kategorie ein Nullobjekt 0, so gibt es zu je zwei Objekten X und Y stets einen kanonischen so genannten Nullmorphismus 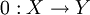$0 : X \to Y$, der die Verkettung von

$X \to 0 \to Y$

ist. In Kategorien mit Nullobjekten gibt es also den Begriff des Kerns eines Morphismus f, definiert als Differenzkern des Paares (f,0).

Nullmorphismen erlauben auch die Konstruktion eines kanonischen Pfeils aus einem Koprodukt in das entsprechende Produkt.