Fremdschlüssel

Ein Schlüssel dient in einer Relationalen Datenbank dazu, die Tupel einer Relation eindeutig zu identifizieren. Anschaulich kann man sich eine Relation als Tabelle vorstellen. Ein Schlüssel für eine solche Tabelle ist dann eine Gruppe von Spalten, die so ausgewählt wird, dass jede Zeile in dieser Gruppe eine einmalige Wertekombination hat.

Einführung

Superschlüssel ⊇ Schlüsselkandidaten, aus diesen wird der Primärschlüssel gewählt

In Relationalen Datenbanken unterscheidet man die Schlüsselbegriffe

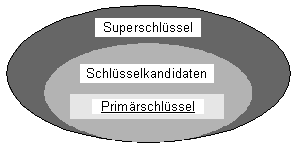
• Superschlüssel: Menge von Attributen (Feldern) in einer Relation (Tabelle), die die Tupel (Zeilen) in dieser Relation eindeutig identifizieren, also bei paarweise ausgewählten Tupeln immer unterschiedliche Werte enthalten (man sagt auch: "eindeutig sind"). Ein trivialer Superschlüssel wäre zum Beispiel die Menge aller Attribute einer Relation gemeinsam (trivial deswegen, weil eine Relation eine Menge von Tupeln ist. Die Elemente von Mengen müssen eindeutig sein, also darf es in einer Relation keine zwei gleichen Tupel geben)
• Schlüsselkandidat (auch Kandidatenschlüssel oder Alternativschlüssel genannt): Eine minimale Teilmenge der Attribute eines Superschlüssels, welche die Identifizierung der Tupel ermöglicht (Schlüsselkandidaten ⊆ Superschlüssel).
• Primärschlüssel: Ein ausgewählter Schlüsselkandidat. Die Werte dieses Schlüssels können in einer anderen Tabelle als Fremdschlüssel verwendet werden.
• Suchschlüssel: Ein Attribut oder eine Attributkombination einer Relation, die als Suchkriterium dient. Ein Suchschlüssel muss nicht notwendigerweise auch ein identifizierender Schlüssel sein. Es können sich also auch mehrere Datensätze über den gleichen Schlüsselwert qualifizieren.
• Sekundärschlüssel oder alternativer Suchschlüssel: Ein Attribut oder eine Attributkombination zur Suche in einer Relation, die kein Primärschlüssel ist. Ein Sekundärschlüssel ist ebenfalls kein Schlüssel im engeren Sinne, da auch nicht identifizierende Attributkombinationen einbezogen werden. In der Fachliteratur ist diese Definition uneinheitlich.
• Fremdschlüssel: Ein Attribut oder eine Attributkombination einer Relation, welches auf einen Primärschlüssel (bzw. Schlüsselkandidat) einer anderen oder der gleichen Relation verweist. Ein Fremdschlüssel in einer Relation R ist in aller Regel kein Schlüssel im engeren Sinne für diese Relation. Es handelt sich aber um einen Sekundärschlüssel.
• sprechender Schlüssel (auch natürlicher Schlüssel genannt): Ein Schlüsselkandidat, der im Tupel auf natürliche Weise vorhanden ist. Ein solcher Schlüssel besitzt also auch in der realen Welt eine Bedeutung, wie z.B. "Fahrgestellnummer" bei polizeilich zugelassenen KFZ.
• stellvertretender Schlüssel (Surrogatschlüssel) Ein künstlich erzeugtes, im Tupel zuvor gar nicht vorkommendes Attribut, das die Tupel der Relation identifiziert. Wird dann häufig als Primärschlüssel herangezogen. Triviales Beispiel: Laufnummer.

Um die Tupel einer Relation eindeutig identifizieren zu können, kommen in der Regel verschiedene Attribute oder Attributkombinationen in Frage: Das sind die Schlüsselkandidaten. Neben der Eigenschaft, die Tupel eindeutig zu identifizieren, muss ein Schlüsselkandidat zusätzlich noch "minimal" sein. Das bedeutet, dass alle an einem Schlüsselkandidaten beteiligten Attribute auch tatsächlich gebraucht werden, damit ein Tupel identifiziert werden kann. Aus allen Schlüsselkandidaten wird einer ausgewählt, der dann bevorzugt zur eindeutigen Referenzierung von einzelnen Tupeln verwendet wird: Der Primärschlüssel. Formal unterscheidet der Primärschlüssel sich in nichts von den übrigen Schlüsselkandidaten.

Die Attributwerte in einem Primärschlüsselattribut können nun verwendet werden, um aus einer anderen Relation heraus (oder sogar aus derselben Relation heraus) auf die zugehörigen Tupel zu verweisen. Ein Attribut, das derartige Verweise enthält, nennt man Fremdschlüssel. Man sagt auch: ein Fremdschlüssel verweist auf einen Primärschlüssel. Mit Hilfe eines Fremdschlüssels, können also Beziehungen zwischen Relationen hergestellt werden.

Unabhängig von der Wahl des Primärschlüssels kann in einer Relation über beliebige Attributkombinationen nach Datensätzen gesucht werden. Das jeweils ausgewählte Suchkriterium nennt man dann "Suchschlüssel". Ein Suchschlüssel kann dann natürlich auch so gewählt werden, dass er nicht mehr identifizierend ist, d.h. dass sich ggf. auch mehrere Tupel für eine gegebene Wertekombination qualifizieren. In aller Regel wird in einer Relation häufig über den Primärschlüssel gesucht. Will man dagegen ausdrücklich zum Ausdruck bringen, dass nicht über den üblichen Primärschlüssel gesucht wird, so spricht man von einem "Sekundärschlüssel".

Formale Definition

Es sei ein bestimmtes Relationenschema R (das Tabellen-Gerüst, d.h. alle Spalten) gegeben. Eine Teilmenge S der Attribute des Schemas R heißt Schlüssel, wenn gilt:

• Eindeutigkeit: Keine Ausprägung von R (keiner der Einträge in der Tabelle) darf zwei verschiedene Tupel (Zeilen) enthalten, bei denen die Werte von S gleich sind.
• Minimalität: Keine echte Teilmenge von S erfüllt bereits die Bedingung der Eindeutigkeit.

Beispiele

a) Literatur ISBN Autor Buchtitel ... 0001 Hans X ... 0002 Peter X ... 0003 Peter Y ... ... ... ... ...

b) Kunden Name Geburtstag Wohnort ... Heinz Hoffmann 01.08.1966 Norden, BBS ... Alf Appel 08.11.1957 Kassel ... Harry Hulimann 27.03.1989 Harem ... ... ... ... ...

c) IstChefVon Vorgesetzter Untergebener 002 104 234 993 234 670 ... ...

a) Hier ist der Schlüssel ein einzelnes Attribut. Die ISBN eignet sich dafür sehr gut, denn keine zwei Bücher haben dieselbe ISBN. Bücher können allerdings sehr wohl den gleichen Titel haben oder vom selben Autor stammen.

Anm: Die ISBN (International Standard Book Number) wird hier nur symbolisch als Laufnummer dargestellt, eine ISBN ist in Wirklichkeit komplizierter aufgebaut.

b) Hier wird ein Teil der Attribute als Schlüssel verwendet. Diese Kundendatenbank geht davon aus, dass es keine Kunden gibt, die denselben Namen tragen und am selben Tag Geburtstag haben.

c) Hier kommen nur alle Attribute der Relation als Schlüssel in Frage. In dieser etwas abstrakteren Relation wird anhand von Personalnummern dargestellt, welcher Angestellte einer Firma der direkte Vorgesetzte welches anderen Angestellten ist.

Superschlüssel

Ein Superschlüssel (auch Oberschlüssel, engl. super key) ist eine beliebige Menge von Attributen, die die Tupel einer Relation eindeutig identifiziert. Die formale Definition lautet:

Ist R(A) eine Relation über der Menge von Attributen A: = {A₁,...,A_n}, so gilt: 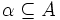$\alpha \subseteq A$ ist genau dann ein Superschlüssel von R, wenn gilt: $\alpha \rightarrow A$.

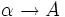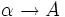Diese Definition setzt den Begriff der funktionalen Abhängigkeit (die Grundlage des Zeichens „$\rightarrow$“) voraus. $\alpha \rightarrow A$ bedeutet: Haben zwei Tupel die gleichen Werte in den Attributen von α, so haben sie auch die gleichen Werte in den Attributen A.

Anhand dieser Definition ergeben sich schon für kleine Anzahlen von Attributen sehr viele Superschlüssel. Für die Beispielrelationen der Einleitung sind dies die folgenden:

a) {ISBN}, {ISBN, Autor}, {ISBN, Autor, Buchtitel}, {Autor, Buchtitel, ...}, {ISBN, Autor, Buchtitel, ...}

b) {Name, Geburtstag}, {Name, Geburtstag, Wohnort}, {Name, Geburtstag, Wohnort, ...}

c) {Vorgesetzter, Untergebener}

Besonders zu beachten ist, dass die Kombination aller Attribute einer Relation immer einen Superschlüssel bildet. Das kommt daher, dass Relationen keine zwei völlig identischen Tupel enthalten dürfen - denn eine Relation ist prinzipiell eine Menge und nach der Mengenlehre darf eine solche keine zwei identischen Elemente enthalten. Des Weiteren sind in dieser oft unüberschaubaren Menge auch die „praktischeren“ Schlüsselkandidaten enthalten. Der Begriff des Superschlüssels spielt allerdings bei den Definition der Normalformen 3. Normalform (3NF) und Boyce-Codd-Normalform (BCNF) eine wichtige Rolle.

Schlüsselkandidat

Ein Schlüsselkandidat (engl. candidate key) ist eine minimale Menge von Attributen, die die Tupel (Datensatz) einer Relation eindeutig identifiziert. Die formale Definition lautet:

Ist R(A) eine Relation über der Menge von Attributen A: = {A₁,...,A_n}, so gilt: 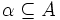$\alpha \subseteq A$ ist genau dann ein Schlüsselkandidat von R, wenn gilt: $\alpha \dot \rightarrow A$.

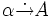Hierbei wird der Begriff der vollen funktionalen Abhängigkeit - dargestellt durch 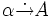$\alpha \dot \rightarrow A$ - verwendet. Hier ist A von α voll funktional abhängig, was bedeutet:

1. Haben zwei Tupel in den Schlüsselattributen (α) dieselben Werte, so haben sie auch in allen übrigen Attributen (A) dieselben Werte. Und:
2. Entfernt man ein Attribut aus α, so gilt Eigenschaft 1 nicht mehr.

Im Gegensatz zum Superschlüssel werden hier also nur noch diejenigen Attributmengen betrachtet, die nicht mehr verkleinert werden können, ohne ihre Schlüsseleigenschaft zu verlieren; man sagt auch, sie seien minimal identifizierend. Für die Beispielrelationen der Einleitung ergeben sich folgende Schlüsselkandidaten:

a) {ISBN}, {Autor, Buchtitel, ...}

b) {Name, Geburtstag}

c) {Vorgesetzter, Untergebener}

Aus der Liste der Superschlüssel wurden also gerade diejenigen ausgewählt, die minimal sind. Gelegentlich wird auch die Bezeichnung Kandidatenschlüssel verwendet, was eine wörtliche Übersetzung des englischen Fachbegriffs candidate key ist.

Primärschlüssel und Sekundärschlüssel

Um mitzuteilen, welchen der Schlüsselkandidaten man zur Identifikation der Tupel in einer Relation bevorzugt, wird aus allen Schlüsselkandidaten der Primärschlüssel ausgewählt. Der Primärschlüssel wird üblicherweise so ausgewählt, dass er möglichst klein ist, d.h. möglichst wenige Attribute umfasst. Darüber hinaus muss der ausgewählte Primärschlüssel tatsächlich die eindeutige Identifizierbarkeit der realen Objekte erlauben, die durch die Tupel der Relation repräsentiert werden. Wählt man beispielsweise die Kombination {Name, Geburtstag} als Primärschlüssel aus, so legt man damit auch fest, dass es keine zwei gleichnamigen Personen geben darf, die am gleichen Tag Geburtstag haben. Durch die Einführung von Surrogatschlüsseln wird dieses Problem in jedem Fall vermieden. Für die Beispielrelationen aus der Einleitung bieten sich die folgenden Primärschlüssel an:

a) {ISBN}

b) {Name, Geburtstag}

c) {Vorgesetzter, Untergebener}

Bei den Beispielen b) und c) ist die Entscheidung müßig, denn es gibt jeweils nur einen Schlüsselkandidaten, folglich muss dieser auch als Primärschlüssel verwendet werden. In Beispiel a) entscheidet man sich für {ISBN} als Primärschlüssel, weil dies der kleinste Schlüssel ist (er hat im Gegensatz zu {Autor, Buchtitel, ...} nur ein Attribut), zudem wird dadurch die Realität genau wiedergegeben. Besteht ein Primärschlüssel aus mehreren Attributen, spricht man auch von einem kombinierten Primärschlüssel oder einem Verbundschlüssel. Durch die Auswahl des Primärschlüssels werden alle anderen Schlüsselkandidaten der Relation automatisch zu Sekundärschlüsseln. In unseren Beispielrelationen wären dies:

a) {Autor, Buchtitel, ...}

b) {Wohnort}

c) keine

Sekundärschlüssel werden hauptsächlich dazu verwendet, effiziente Sekundärindizes zu erzeugen; ein Sekundärindex ist eine optionale Suchstruktur einer Datenbank, um Tupel schneller zu finden. Sekundärschlüssel müssen nicht notwendigerweise eindeutig sein, obwohl die nicht zum Primärschlüssel erhobenen, verbliebenen Schlüsselkandidaten es natürlich sind. Aber auch Fremdschlüssel sind Sekundärschlüssel, weil sie dazu dienen Datensätze zu beschreiben (ordnen, gruppieren etc.).

Stellvertretender Schlüssel

Eigener Artikel siehe Surrogatschlüssel

Es ist möglich, dass alle Schlüsselkandidaten einer Relation aus mehreren Attributen bestehen, oder dass alle Schlüsselkandidaten die tatsächlichen Verhältnisse nur unzureichend widerspiegeln. Von unseren Beispielen ist b) ein solcher Fall. Will man hier eine Person identifizieren, muss man stets Name und Geburtstag gleichzeitig angeben; das ist für die Datenbank umständlich, denn es wird Speicherplatz verschwendet und es müssen stets zwei Attribute verglichen werden, was zu unnötiger Mehrarbeit führt. Es ist daher oft wünschenswert, ein zusätzliches Attribut einzuführen, das als Primärschlüssel dient: Man nennt dies einen stellvertretenden Schlüssel (engl. surrogate key). Für Beispiel b) würden sich hier allgemeine Attribute wie „Personalausweis-Nummer“ oder geschäftseigene Identifikationsnummern wie „Kundennummer“ anbieten. Übrigens ist auch die ISBN aus a) ein surrogate key, ein künstlicher Schlüssel, der von den Buchverlagen eingeführt wurde, um die Identifikation von Büchern zu erleichtern.

Fremdschlüssel

Ein Primärschlüssel einer Relation kann Fremdschlüssel einer anderen werden

Ein Fremdschlüssel ist ein Sekundärschlüssel einer Relation, der in einer anderen Relation Primärschlüssel oder Schlüsselkandidat ist.

Er dient als Verweis zwischen zwei Relationen, d.h. er zeigt an, welche Tupel der Relationen inhaltlich miteinander in Verbindung stehen. Beispiele für Fremdschlüssel sind die beiden Attribute „Vorgesetzter“ und „Untergebener“ aus der Beispielrelation c) der Einleitung: Hier wird jeweils die „Personalnummer“ eines Angestellten angegeben. Doch mit einer solchen Nummer lässt sich im Alltag eher wenig anfangen; viel wichtiger sind Name, Abteilung, Beschäftigung und ähnliche Informationen. Deshalb wird hier höchstwahrscheinlich eine weitere Relation existieren, die Attribute wie {Personalnummer, Name, Abteilung, Beschäftigung, ...} enthält. Diese Relation wird ebenso höchstwahrscheinlich den Primärschlüssel {Personalnummer} besitzen; es bietet sich also an, Personalnummer als Fremdschlüssel zu benutzen.

Definition

Seien R, S Relationen und die Attributmenge α der Primärschlüssel von R. Wenn eine kompatible Attributmenge β aus S ein Fremdschlüssel bzgl. α sein soll, so müssen die Werte von β Teilmenge der Werte des Primärschlüssels α in R sein. (vgl. referentielle Integrität)

Eine Attributmenge ist dann kompatibel zu einer anderen, wenn die Wertebereiche der beteiligten Attribute gleich sind, also dom(α) = dom(β).

Fremdschlüssel und Beziehungstypen

In der Datenbankwelt unterscheidet man verschiedene Arten von Beziehungen zwischen zwei Relationen R und S. Im Falle relationaler Datenbanken werden die folgenden Beziehungsarten unterschieden:

1. 1:1-Beziehung, einem Datensatz aus R ist bis zu 1 anderer aus S zugeordnet, der aus S genau einem aus R
2. 1:n-Beziehung, einem Datensatz aus R sind einer oder mehrere andere Datensätze aus S zugeordnet, jedem aus S aber genau einer aus R
3. n:m-Beziehung, einem Datensatz aus R können einer oder mehrere aus S zugeordnet sein, und einem aus S mehrere aus R

(Fall n/mc = keiner, einer oder mehrere)

Die Fälle 1. und 2. werden implementiert, indem S den Primärschlüssel aus R als Fremdschlüssel enthält. Im Falle der 1:1-Beziehung wird dies auch der Primärschlüssel. Für die n:m-Beziehung braucht man, wie in Beispiel c) oben, eine eigene Relation, die die Primärschlüssel beider Relationen als Fremdschlüssel erhält. Beide Attributmengen zusammen sind der Primärschlüssel dieser "Verknüpfungsrelation".

Hinweis: Die eigentlichen sog. Kardinalitäten dieser drei Beziehungstypen sind [1,1]:[0,1], [1,1]:[0,*], [0,*]:[0,*]. "*" steht für "beliebig viele".

Siehe auch

• Attribut
• Integritätsbedingung
• Referenzielle Integrität
• Schlüssel (Informatik)
• Suche

Literatur

• Andreas Heuer, Gunter Saake: Datenbanken. Konzepte und Sprachen. MITP Verlag, ISBN 3-8266-0619-1
• A. Eickler, A.Kemper: Datenbanksysteme. Oldenbourg Verlag, ISBN 3-486-27392-2