- Irreguläre Primzahl
-
Im mathematischen Teilgebiet der Zahlentheorie heißt eine Primzahl regulär, wenn sie kein Teiler von bestimmten Zahlen ist. E. Kummer konnte zeigen, dass der große Fermatsche Satz für Exponenten, die durch eine reguläre Primzahl teilbar sind, wahr ist.
Inhaltsverzeichnis
Definition
Eine Primzahl p > 2 heißt regulär, wenn sie keine der Bernoulli-Zahlen
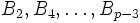 teilt (d.h. wenn die Zähler dieser Zahlen in vollständig gekürzter Darstellung nicht durch p teilbar sind).
teilt (d.h. wenn die Zähler dieser Zahlen in vollständig gekürzter Darstellung nicht durch p teilbar sind).Man kann zeigen, dass diese Bedingung äquivalent ist zur folgenden: Eine Primzahl heißt regulär, wenn die Klassenzahl des p-ten Kreisteilungskörpers nicht durch p teilbar ist.
Eigenschaften und Wissenswertes
Es ist bekannt, dass es unendlich viele irreguläre Primzahlen gibt. Die kleinsten irregulären Primzahlen sind 37, 59, 67 (Folge A000928 in OEIS). Es ist unbekannt, ob es unendlich viele reguläre Primzahlen gibt (Folge A007703 in OEIS); man vermutet, dass
 aller Primzahlen regulär sind.
aller Primzahlen regulär sind.Reguläre Primzahlen
Die ersten Glieder der Folge: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 43, 47, 53, 61, ...
Irreguläre Primzahlen
Die ersten Glieder der Folge: 37, 59, 67, 101, 103, 131, 149, 157, 233, 257, 263, 271, 283, 293, 307, ...
Anwendung auf den großen Satz von Fermat
Es sei p eine reguläre Primzahl, und es gelte ap + bp = cp mit teilerfremden ganzen Zahlen a,b,c, wobei keine der Zahlen a,b,c durch p teilbar sei (diese Bedingung wird "Fall I" genannt). Bezeichnet ζ eine primitive p-te Einheitswurzel, so lässt sich die linke Seite der Gleichung faktorisieren als
und man kann zeigen, dass diese Faktoren paarweise teilerfremd sind. Da ihr Produkt cp eine p-te Potenz ist, sind auch die einzelnen Faktoren p-te Potenzen von Idealen im Ganzzahlring
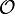 des Kreisteilungskörpers
des Kreisteilungskörpers  , insbesondere also
, insbesondere alsoAn dieser Stelle kann nun die Regularität von p verwendet werden: Die p-te Potenz dieses Ideals
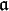 ist ein Hauptideal, also ist auch
ist ein Hauptideal, also ist auch 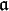 selbst ein Hauptideal, d.h. es gibt eine Einheit u und ein Element
selbst ein Hauptideal, d.h. es gibt eine Einheit u und ein Element  , so dass
, so dassgilt. Diese Aussage kann durch Kongruenzbetrachtungen modulo p zum Widerspruch gebracht werden.
Weblinks
Wikimedia Foundation.



