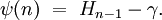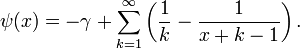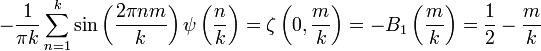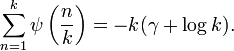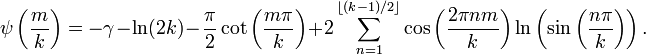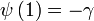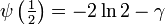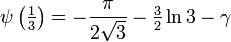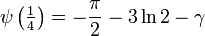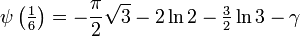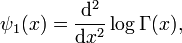- Gaußsche Psi-Funktion
-
Die Digamma-Funktion ist in der Mathematik eine Funktion, die definiert wird als:
Sie ist also die logarithmische Ableitung der Gammafunktion. Die Digamma-Funktion ist die erste der Polygammafunktionen.
Inhaltsverzeichnis
Berechnung
Die Beziehung zu der harmonischen Reihe
Die Digammafunktion, welche meist als ψ0(x), ψ0(x) oder
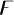 (nach der Form des veralteten griechischen Buchstaben Ϝ digamma) dargestellt wird, steht mit der harmonischen Reihe in folgender Beziehung:
(nach der Form des veralteten griechischen Buchstaben Ϝ digamma) dargestellt wird, steht mit der harmonischen Reihe in folgender Beziehung:wobei Hn das n-te Element der harmonischen Reihe und γ die Euler-Mascheroni-Konstante ist. Für halbzahlige Werte kann sie geschrieben werden als
Integral-Darstellung
Die Digammafunktion kann wie folgt als Integral dargestellt werden:
Dies kann auch geschrieben werden als
Dies folgt aus der Formel für das Euler-Integral für die harmonische Reihe.
Taylor-Reihe
Durch Reihenentwicklung der Taylor-Reihe um den Punkt z=1 kann die Digammafunktion wie folgt dargestellt werden
Sie konvergiert für |z|<1. Dabei ist ζ(n) die Riemannsche ζ-Funktion. Die Reihe kann leicht von der zugehörigen Taylor-Reihe für die Hurwitzsche ζ-Funktion hergeleitet werden.
Binomische Reihe
Die Binomische Reihe für die Digammafunktion folgt aus dem Euler-Integral
wobei
der Binomialkoeffizient ist.
Spiegelgleichung
Die Digammafunktion genügt folgender Spiegelgleichung, welche der der Gammafunktion ähnelt:
Hiermit kann allerdings nicht ψ(1/2) berechnet werden; dieser Wert ist unten angegeben.
Rekursionsformel
Die Digamma-Funktion genügt der Rekursionsformel
oder
wobei Δ der rechtsseitige Differenzoperator ist. Dies erfüllt die Rekursionsbeziehung der harmonischen Reihe. Daraus folgt
Allgemeiner gilt:
Gaußsche Summe
Die Digammafunktion hat eine Gaußsche Summe der Form
für natürliche Zahlen 0 < m < k. Dabei ist ζ(s,q) die Hurwitzsche ζ-Funktion und Bn(x) eine Bernoulli-Zahl. Ein Spezialfall des Multiplikationstheorem ist
Gaußsches Digamma-Theorem
Für ganze Zahlen m und k (mit m < k), kann die Digammafunktion mit elementaren Funktionen ausgedrückt werden
Besondere Werte
Die Digamma-Funktion hat folgende besondere Werte:
Ableitung
Die Ableitung der Digammafunktion ist nach deren Definition die Trigamma-Funktion
die zweite Polygammafunktion.
Literatur
- Milton Abramowitz und Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4. Siehe §6.3
Weblinks
- Eric W. Weisstein: Digamma Function auf MathWorld (englisch)
Wikimedia Foundation.

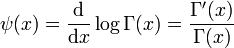
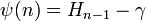
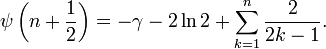
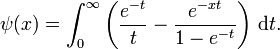
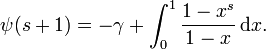
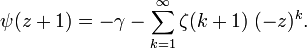
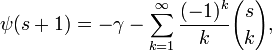

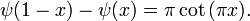
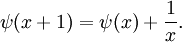
![\Delta [\psi] (x) = \frac{1}{x},](/pictures/dewiki/98/bb8c8ce5288f89c64c7cc30d51f1de2a.png)