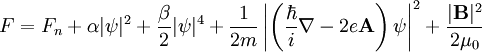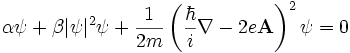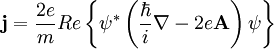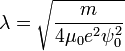Ginzburg-Landau-Theorie

Die Ginzburg-Landau-Theorie (nach Lew Dawidowitsch Landau und Witali Lasarewitsch Ginsburg) ist eine Theorie zur Beschreibung der Supraleitung. Im Gegensatz zur BCS-Theorie, die eine Erklärung auf mikroskopischer Basis anstrebt, untersucht sie die makroskopischen Eigenschaften von Supraleitern mit Hilfe von allgemeingültigen thermodynamischen Argumenten. Es handelt sich also um eine phänomenologische Theorie, die schon zum Zeitpunkt ihrer Aufstellung, 1950, richtig war (nur dass ursprünglich anstelle von 2e, der Ladung der Cooper-Paare, ein allgemeinerer Ladungsparameter q gewählt wurde). Später, 1959, konnte die phänomenologische Theorie aus der BCS-Theorie hergeleitet werden, wobei man insbesondere die Identifikation 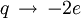$q\,\rightarrow\,-2e$ erkannte.

Aufbauend auf Landaus Theorie der Phasenübergänge zweiter Ordnung argumentierten Landau und Ginsburg, dass die freie Energie F eines Supraleiters nahe dem Phasenübergang durch einen komplexen Ordnungsparameter ψ ausgedrückt werden kann. Dieser beschreibt, inwieweit sich das System im supraleitenden Zustand befindet. ψ = 0 entspricht dem Normalzustand. Die freie Energie lautet dann

$F = F_n + \alpha |\psi|^2 + \frac{\beta}{2} |\psi|^4 + \frac{1}{2m} \left| \left(\frac{\hbar}{i}\nabla - 2e\mathbf{A} \right) \psi \right|^2 + \frac{|\mathbf{B}|^2}{2\mu_0}$

wobei F_n die freie Energie im Normalzustand bezeichnet, α und β sind phänomenologische Parameter, 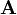$\mathbf A$ ist das Vektorpotential und 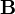$\mathbf B$ ist die magnetische Induktion, die mit 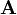$\mathbf A$ über die bekannte Beziehung 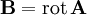$\mathbf B ={\rm rot}\,\mathbf A$ zusammenhängt. Die Minimierung der freien Energie hinsichtlich der Schwankungen des Ordnungsparameters und des Vektorpotentials führt auf die Ginsburg-Landau-Gleichungen

$\alpha \psi + \beta |\psi|^2 \psi + \frac{1}{2m} \left(\frac{\hbar}{i}\nabla - 2e\mathbf{A} \right)^2 \psi = 0$

$\mathbf{j} = \frac{2e}{m} Re \left \{ \psi^* \left(\frac{\hbar}{i}\nabla - 2e \mathbf{A} \right) \psi \right \}$

Dabei bezeichnet j den Strom und Re den Realteil. Die erste Gleichung weist interessante Ähnlichkeiten zur zeitunabhängigen Schrödingergleichung auf (man beachte aber, dass ψ hier nicht wie in der Quantenmechanik eine Wahrscheinlichkeitsamplitude ist, sondern die angegebene quasi-klassische Bedeutung hat ( | ψ | ² ist die Dichte der Träger der Supraleitung, der Cooper-Paare ). Mathematisch handelt es sich um eine zeitunabhängige Gross-Pitaevskii-Gleichung, welche eine nichtlineare Verallgemeinerung der Schrödingergleichung ist. Die erste Gleichung bestimmt also den Ordnungsparameter ψ als Funktion des angelegten Magnetfelds. Die zweite Gleichung gibt den Suprastrom an und entspricht der London-Gleichung.

Aus den Ginsburg-Landau-Gleichungen lassen sich viele interessante Ergebnisse ableiten. Das vermutlich bedeutendste ist die Existenz von zwei charakteristischen Längen in Supraleitern. Die erste ist die Kohärenzlänge ξ,

$\xi = \sqrt{\frac{\hbar^2}{2 m |\alpha|}}$.

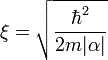Diese beschreibt die Größe der thermodynamischen Fluktuationen in der supraleitenden Phase. Die zweite ist die Eindringtiefe λ,

$\lambda = \sqrt{\frac{m}{4 \mu_0 e^2 \psi_0^2}}$

wobei ψ₀ den Ordnungsparameter im Gleichgewicht, ohne elektromagnetisches Feld, bezeichnet. Die Eindringtiefe gibt die Tiefe wieder, bis zu der ein externes Magnetfeld in den Supraleiter eindringen kann.

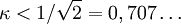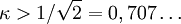Das Verhältnis κ = λ/ξ wird auch als Ginsburg-Landau-Parameter bezeichnet. Abhängig von der Größe dieses Parameters lassen sich Supraleiter in zwei Klassen mit unterschiedlichen physikalischen Eigenschaften einteilen. Typ I-Supraleiter sind solche mit $\kappa < 1/\sqrt 2 = 0,707 \dots$. Ist $\kappa > 1/\sqrt 2 = 0,707 \dots$ , so ist der Supraleiter vom Typ II. Dieses Ergebnis lässt sich mittels einer dualen Ginsburg-Landau-Theorie für Supraleiter herleiten (siehe Kapitel 13 des dritten Buchs). Es handelt sich in beiden Fällen um einen Phasenübergang zweiter Ordnung.

Ein weiteres wichtiges Ergebnis der Ginsburg-Landau-Theorie wurde durch Alexei Alexejewitsch Abrikossow 1957 gefunden. In einem Typ II-Supraleiter in einem hohen Magnetfeld dringt das Feld in Form von Kanälen mit quantisiertem Fluss ein. Diese sogenannten Flussfäden oder Flussschläuche (en:vortex) bilden ein – oft hexagonales – (Abrikossow-)Gitter.

Diese Theorie ergibt sich als Skalierungsgrenzwert (en:scaling limit) des XY-Modells.

Formal besteht eine große Ähnlichkeit in der phänomenologischen Beschreibung der Supraleitung durch Ginzburg und Landau und dem Higgs-Kibble-Mechanismus in der Hochenergiephysik: Der Meißner-Ochsenfeld-Effekt der Supraleitung, der auf die Erzeugung einer endlichen Eindringtiefe λ der magnetischen Induktion hinausläuft, entspricht der Massenerzeugung der Eichfelder A^α der Hochenergiephysik, wenn man die übliche Übersetzung 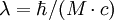$\lambda =\hbar /(M\cdot c)$ benutzt ( 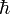$\hbar$ ist dabei das Plancksche Wirkungsquantum, geteilt durch 2π, und c die Lichtgeschwindigkeit; das heißt: die Eindringtiefe wird als Compton-Wellenlänge einer Masse M identifiziert ).

Ausgewählte Veröffentlichungen

• V.L. Ginzburg und L.D. Landau, Zh. Eksp. Teor. Fiz. 20, 1064 (1950)
• A.A. Ginzburg, Zh. Eksp. Teor. Fiz. 32, 1442 (1957)
• L.P. Gor'kov, Sov. Phys. JETP 36, 1364 (1959)

Bücher

• D. Saint-James, G. Sarma and E. J. Thomas, Type II Superconductivity Pergamon (Oxford 1969)
• M. Tinkham, Introduction to Superconductivity, McGraw-Hill (New York 1996)
• Hagen Kleinert, Gauge Fields in Condensed Matter, Vol. I World Scientific (Singapore, 1989); Paperback ISBN 9971-5-0210-0 (auch erhältlich online hier)
• Pierre-Gilles de Gennes, Superconductivity of Metals and Alloys, W. A. Benjamin, 1964, [ISBN 0-7382-0101-4]