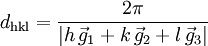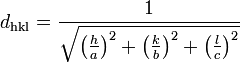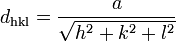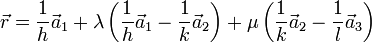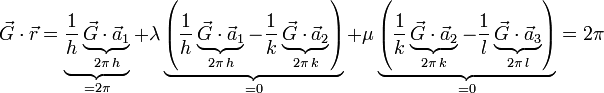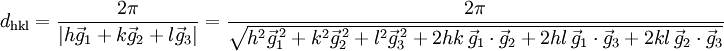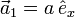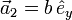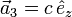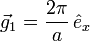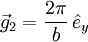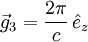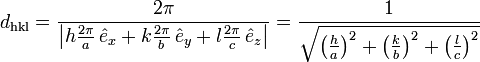Gitterebenenabstand

Als Netz- oder Gitterebene bezeichnet man eine Ebene, die durch Punkte des Kristallgitters aufgespannt wird. Ihre Lage im Raum wird durch die Millerschen Indizes (hkl) beschrieben.

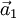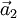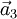Ein Kristallgitter lässt sich als ganzzahlige Linearkombination der Basisvektoren $\vec{a}_1$, $\vec{a}_2$ und $\vec{a}_3$ (Richtung der Kristallachsen) beschreiben. Eine Netzebene ist durch ihre Schnittpunkte mit den Kristallachsen festgelegt. 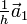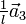Die Millerschen Indizes (hkl) bezeichnen die Ebene, die durch die drei Punkte $\tfrac{1}{h} \vec{a}_1$, $\tfrac{1}{k} \vec{a}_2$ und $\tfrac{1}{l} \vec{a}_3$ geht. Also schneiden die Kristallachsen des jeweiligen Kristallsystems die Ebenen gerade an den Kehrwerten der einzelnen Indizes. Ein Index von Null bezeichnet dabei einen Schnittpunkt im Unendlichen, d.h. der zugehörige Basisvektor ist parallel zur Ebene.

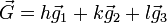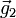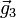Der reziproke Gittervektor $\vec{G}=h \vec{g}_1 + k \vec{g}_2 + l \vec{g}_3$ steht senkrecht auf der durch die Millerschen Indizes (hkl) definierten Netzebene. Die Vektoren $\vec{g}_1$, $\vec{g}_2$ und $\vec{g}_3$ bilden die Basisvektoren des reziproken Gitters.

Eine Netzebenenschar besteht aus allen parallel verlaufenden Netzebenen mit jeweils dem Netzebenenabstand d_hkl. Dieser kann aus den Millerschen Indizes und den reziproken Gittervektoren berechnet werden:

$d_{\mathrm{hkl}}=\frac{2\pi}{|h\,\vec{g}_{1}+k\,\vec{g}_{2}+l\,\vec{g}_{3}|}$

Für Kristallsysteme mit rechtwinkligen Achsen, also orthorhombische und höher symmetrische Gitter (tetragonal und kubisch) gilt folgende Formel (a, b, c seien die Gitterkonstanten):

$d_{\mathrm{hkl}}=\frac{1}{\sqrt{\left(\frac{h}{a}\right)^{2}+\left(\frac{k}{b}\right)^{2}+\left(\frac{l}{c}\right)^{2}}}$

Diese vereinfacht sich beispielsweise für kubische Systeme durch Gleichsetzen von a = b = c weiter:

$d_{\mathrm{hkl}}=\frac{a}{\sqrt{h^{2}+k^{2}+l^{2}}}$

Herleitungen

Eine Ebene ist eindeutig durch drei nicht auf einer Gerade liegende Punkte definiert. Dies sind hier die Schnittpunkte mit den Kristallachsen: 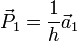$\vec{P}_{1}=\frac{1}{h} \vec{a}_1$, $\vec{P}_{2}=\frac{1}{k} \vec{a}_2$ und $\vec{P}_{3}=\frac{1}{l} \vec{a}_3$.

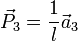Die Punkte auf der Ebene lassen sich durch die Parameterform 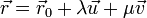$\vec r = \vec r_0 + \lambda \vec u + \mu \vec v$ beschreiben (mit Aufpunkt und zwei Richtungsvektoren, die in der Ebene liegen und nicht kollinear sind). Liegen zwei Punkte in der Ebene, so liegt deren Verbindungsvektor ebenfalls in der Ebene. Hierüber lassen sich die Richtungsvektoren konstruieren (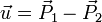$\vec u = \vec P_1-\vec P_2$ und $\vec v = \vec P_2-\vec P_3$). Als Aufpunkt wähle irgendeinen in der Ebene liegenden Punkt (hier $\vec P_1$):

$\vec{r}=\frac{1}{h}\vec{a}_1+\lambda \left(\frac{1}{h}\vec{a}_1 - \frac{1}{k}\vec{a}_2\right) + \mu \left(\frac{1}{k}\vec{a}_2 - \frac{1}{l}\vec{a}_3\right)$

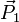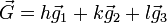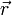Bildet man das Skalarprodukt zwischen dem reziproken Gittervektor $\vec{G}=h\vec{g}_1 + k\vec{g}_2 + l\vec{g}_3$ und $\vec{r}$ unter Ausnutzung der Relation 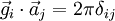$\vec{g}_{i}\cdot\vec{a}_{j}=2\pi \delta_{ij}$, so ergibt sich:

$\vec{G}\cdot\vec{r}=\underbrace{\frac{1}{h}\underbrace{\vec{G}\cdot\vec{a}_{1}}_{2\pi\, h}}_{=2\pi}+\lambda\underbrace{\left(\frac{1}{h}\underbrace{\vec{G}\cdot\vec{a}_{1}}_{2\pi\, h}-\frac{1}{k}\underbrace{\vec{G}\cdot\vec{a}_{2}}_{2\pi\, k}\right)}_{=0}+\mu\underbrace{\left(\frac{1}{k}\underbrace{\vec{G}\cdot\vec{a}_{2}}_{2\pi\, k}-\frac{1}{l}\underbrace{\vec{G}\cdot\vec{a}_{3}}_{2\pi\, l}\right)}_{=0}=2\pi$

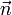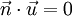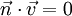Für einen Normalenvektor der Ebene $\vec{n}$ sind die Skalarprodukte mit den Richtungsvektoren gleich Null ($\vec{n}\cdot\vec{u}=0$ und $\vec{n}\cdot\vec{v}=0$). Genau das trifft auf 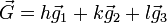$\vec{G}=h\vec{g}_1 + k\vec{g}_2 + l\vec{g}_3$ zu, dieser steht also auf der Ebene (hkl) senkrecht.

Durch den Gitterpunkt am Koordinatenursprung verläuft parallel zur gerade betrachteten Ebene durch P₁ auch eine Ebene mit den Indizes (hkl). Deren Abstand ist die Projektion eines Verbindungsvektors beider Ebenen (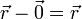$\vec{r}-\vec{0}=\vec{r}$) auf den normierten Normalenvektor ($\vec{G}/G$). Dies ergibt zusammen mit obiger Rechnung den Netzebenenabstand:

$\frac{\vec{G}}{G}\cdot\vec{r}=\frac{2\pi}{|h \vec{g}_1 + k \vec{g}_2 + l \vec{g}_3|}\equiv d_{\mathrm{hkl}}$

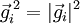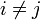Im Nenner treten bei der Betragsbildung sowohl die Längen der reziproken Gittervektoren auf ($\vec{g}_{i}^{\,2}=|\vec{g}_{i}|^{2}$) als auch die Projektionen der Gittervektoren aufeinander ($\vec{g}_{i}\cdot\vec{g}_{j}$ mit $i\neq j$). Letztere sind bei nicht-orthogonalen Kristallsystemen ungleich Null:

$d_{\mathrm{hkl}}=\frac{2\pi}{|h\vec{g}_{1}+k\vec{g}_{2}+l\vec{g}_{3}|}=\frac{2\pi}{\sqrt{h^{2}\vec{g}_{1}^{\,2}+k^{2}\vec{g}_{2}^{\,2}+l^{2}\vec{g}_{3}^{\,2}+2hk\,\vec{g}_{1}\cdot\vec{g}_{2}+2hl\,\vec{g}_{1}\cdot\vec{g}_{3}+2kl\,\vec{g}_{2}\cdot\vec{g}_{3}}}$

Ein orthorhombisches Kristallsystem ist ein rechtwinkliges Kristallsystem mit drei 90°-Winkeln, jedoch ohne gleichlange Achsen. Die Gittervektoren lauten hier ausgedrückt bzgl. der kanonischen Einheitsbasis:

$\vec{a}_1=a\,\hat{e}_x$

$\vec{a}_2=b\,\hat{e}_y$

$\vec{a}_3=c\,\hat{e}_z$

Und die dazugehörigen reziproken Gittervektoren sind ebenfalls orthogonal (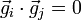$\vec{g}_{i}\cdot\vec{g}_{j}=0$ für $i\neq j$):

$\vec{g}_1=\frac{2\pi}{a}\,\hat{e}_x$

$\vec{g}_2=\frac{2\pi}{b}\,\hat{e}_y$

$\vec{g}_3=\frac{2\pi}{c}\,\hat{e}_z$

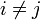Setze diese in obige allgemeine Formel für den Netzebenenabstand ein:

$d_{\mathrm{hkl}}=\frac{2\pi}{\left|h\frac{2\pi}{a}\,\hat{e}_x + k\frac{2\pi}{b}\,\hat{e}_y + l\frac{2\pi}{c}\,\hat{e}_z\right|} = \frac{1}{\sqrt{\left(\frac{h}{a}\right)^{2}+\left(\frac{k}{b}\right)^{2}+\left(\frac{l}{c}\right)^{2}}}$

Das kubische Kristallsystem ist ebenfalls rechtwinklig, aber zusätzlich sind die Gitterkonstanten bzgl. jeder Kristallachse gleich a = b = c und die Formel vereinfacht sich weiter zu:

$d_{\mathrm{hkl}}=\frac{a}{\sqrt{h^{2}+k^{2}+l^{2}}}$