Gradus

Das römische Maßsystem basiert − wie alle vordezimalmetrischen Maße − auf der Nippur-Elle, bzw. dann auch auf den mesopotamischen, ägyptischen und griechischen Systemen.

Das römische Maßsystem galt im ganzen Römisches Reich und wirkt bis heute in vielen späteren Einheiten fort, z. B. in den englischen Maßen. So verhält sich der englische Fuß zum römischen Fußes wie 36 zu 35. Die Ratio des römischen Fußes zum kyrenaischen Fuß beträgt 24 zu 25.

Die Bezeichnung „römischer Fuß“ ist eigentlich post-anachronistisch, weil eben dieser Fuß bereits 2000 Jahre vor Rom den alten Ägyptern als ägyptischer Nippurfuß geläufig war.

Längenmaße

Römische Längenmaße												Fuß
digitus		Fingerbreit	=	¼	palmus	=	18,	522		mm		16−1
palmus		Handbreit	=	¼	pes	=	74,	088		mm		4−1
pes		Fuß	=	4/7	Nippur-Elle	=	296,	352		mm		1
cubitus		Elle	=	1½	pes	=	444,	528		mm		1½
gradus		Einzelschritt	=	2½	pes	=	740,	880		mm		2½
passus		Doppelschritt	=	2	gradi	=	1,	48176		m		5
pertica		Rute	=	2	passus	=	2,	96352		m		10
actus		Arpent	=	12	perticae	=	35,	56224		m		120
stadium		Stadion	=	1/8	mille passus	=	185,	22		m		625
mille passus		Meile	=	1000	passus	=	1,	48176		km		5000
leuga		Leuge	=	1½	milia passuum	=	2,	22264		km		7500

Man beachte, dass der Plural der römischen Meile korrekt milia passuum lautet. Alternativ kann die Meile auch mit „Meilenstein“, milliarium (Plural milliaria) bezeichnet werden.
Statistisch ist der römische Fuß 296,2 ±0,5 mm lang. Der 7-glatte Wert der Nippur-Elle ist genau 518,616 Millimeter; daher umfasst ein römischer Fuß 296,352 mm, also ca. 29,64 cm.
In der römischen Antike wurde der Fuß nicht durch zwölf, d. h. in Zoll geteilt, sondern praktisch ausschließlich in digiti, ein sechzehntel Fuß.

Flächenmaße

Römische Flächenmaße										Acker
pes quadratus	Quadratfuß	=	1	Quadratfuß	=	878,	245079	cm²		14400−1
scripulum	Quadratrute	=	100	Quadratfuß	=	8,	78245079	m²		144−1
actus minimus	Ulne Furchen*	=	1/30	Acker	=	42,	155763792	m²		30−1
clima	Stückchen	=	1/4	Acker	=	316,	16822844	m²		4−1
actus quadratus	Acker	=	1	Quadratarpent	=	1264,	67291376	m²		1
iugerum	Joch	=	2	Acker	=	2529,	34582752	m²		2
heredium	Morgen	=	2	Joch	=	5058,	69165504	m²		4
centuria	Großhufe	=	100	Morgen	=	50,	5869165504	ha		400
saltus	Quadruplex	=	4	Großhufe	=	2,	023476662016	km²		1600

 *  Gleich Breite: 4 Fuß, mal eine Ackerlänge.

Der Acker ist das Quadratarpent (1 Arpent = 12 Zehn-Fuß-Ruten). Das entspricht 14 400 Quadratfuß oder 144 Quadratruten, also etwa einem Achtel Hektar.

Volumen

Flüssigmaße

Römische Flüssigmaße							7-glatter Wert			Sester
ligula	Löffelvoll	=	1/4	Dose	=	11,	296 427 329 152	ml		48−1
cyathus	Dose	=	1/2	Sechstelsester	=	45,	185 709 316 608	ml		12−1
sextans	Sechstelsester	=	1/6	Sester	=	90,	371 418 633 216	ml		6−1
triens	Drittelsester	=	1/3	Sester	=	180,	742 837 266 432	ml		3−1
hemina	Hemine	=	1/2	Sester	=	271,	114 255 899 648	ml		2−1
cheonix	Cheonix	=	2	Drittelsester	=	361,	485 674 532 864	ml		⅔
sextarius	Sester	=	1/6	Kanne	=	542,	228 511 799 296	ml		1
congius	Kanne	=	1/4	Urne	=	3,	253 371 070 795 776	l		6
urna	Urne	=	1/2	Amphore	=	13,	013 484 283 183 104	l		24
amphora	Amphore	=	1	Kubikfuß	=	26,	026 968 566 366 208	l		48
culleus	Schlauch	=	20	Amphoren	=	520,	539 371 327 324 160	l		960

Die Amphore („amphora quadrantal“) entspricht dem Kubikfuß. Die Kanne ist zwei Handbreit im Kubik, sie enthält genau sechs Sestern. Daher ihr Name: Sester, ein sechstel Congius.

Getreidemaße

Römische Getreidemaße							7-glatter Wert			Metze
acetabulum	Schöpflöffel	=	1/2	Viertelsester	=	67,	778 563 974 912	ml		128−1
quartarius	Viertelsester	=	1/2	Hemine	=	135,	557 127 949 824	ml		64−1
hemina	Hemine	=	1/2	Sester	=	271,	114 255 899 648	ml		32−1
sextarius	Sester	=	1/8	Gallone	=	542,	228 511 799 296	ml		16−1
semodius	Gallone*	=	1/2	Metze	=	4,	337 828 094 394 368	l		2−1
modius	Metze	=	1/3	Scheffel	=	8,	675 656 188 788 736	l		1
quadrantal	Scheffel	=	1	Kubikfuß	=	26,	026 968 566 366 208	l		3

* wörtlich:  halbe Metze

Der römische Scheffel misst einen Kubikfuß; wie die Amphore fast 26,027 Liter. Der Drittelscheffel ist die römische Metze, das „Maß“.
Die besonders in Ägypten für Getreide verwendete Artabe entsprach wohl 4½ römischen Metzen, d. h. 1½ römischen Kubikfuß, ca. 39 l.

Gewichte

Die folgende Tabelle bezieht sich auf einen willkürlich festgelegten sieben-glatten Wert zu genau 47,04000 Milligramm für das römische Gerstenkorn; siehe unten für Versuche zur Bestimmung des historischen Werts (der Libra).

Römische Gewichte						7-glatter Wert			Gran	Chalkus	Obolus	Drachme	Unze	Pfund	Mina
granum	Gran	=	1/3	Chalkus	=	47,04000	mg		1	⅔	12−1	72−1	576−1	6912−1	9216−1
chalcus	Chalkus	=	1/8	Obolus	=	70,56000	mg		1½	1	8−1	48−1	384−1	4608−1	6144−1
siliqua	Siliqua	=	1/3	Obolus	=	188,16000	mg		4	2⅔	3−1	18−1	144−1	1728−1	2304−1
obolus	Obolus	=	1/2	Skrupel	=	564,48000	mg		12	8	1	6−1	48−1	576−1	768−1
scrupulum	Skrupel	=	1/3	Drachme	=	1,12896	g		24	16	2	3−1	24−1	288−1	384−1
drachma	Drachme	=	1/2	Schelkel	=	3,38688	g		72	48	6	1	8−1	96−1	128−1
sicilicus	Schekel	=	2	Drachmen	=	6,77376	g		144	96	12	2	4−1	48−1	64−1
uncia	Unze	=	4	Schekel	=	27,09504	g		576	384	48	8	1	12−1	16−1
libra	Pfund	=	12	Unzen	=	325,14048	g		6912	4608	576	96	12	1	3/4
mina	Mine	=	16	Unzen	=	433,52064	g		9216	6144	768	128	16	4/3	1

Das Gewicht der Libra

Seit der Renaissance bis in die Gegenwart wurden unzählige Versuche unternommen den historischen Wert der römischen Libra genauer zu bestimmen.

Die schwere Libra

Im Jahr 1838 schlug August Böckh vor, dass das römische Pfund 6165 französischen Grän entspricht.^[1] Das ergibt einen Wert von (1/18.82715) × 6165 gleich ca. 327,453 g. Dieser Wert wurde im Jahr 1856 von Theodor Mommsen in seinem Ersten Buch zur Römischen Geschichte übernommen,^[2] sowie später auch in seinem Werk „Geschichte des römischen Münzwesens“, Berlin, 1860. Er gilt seither und daher als quasi-unumstößlicher Standardwert für das römische Pfund. Die Hypothese einer schweren Libra läuft aber letztlich auf die Existenz eines  – nicht ganz auszuschließenden, eben 1024 Tausendstel römische Fuß betragenden –  „griechisch-römischen Gewichtsfußes“ hinaus.  Da folgendes gilt:

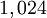
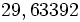
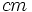
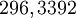
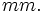$\sqrt[3] {(1/18.82715) * 6165 * (4/3) * 64}$   $\ /$   $\ 1,024$   $\ =$   $\ 29,63392$   $\ cm$   $\ =$   $\ 296,3392$   $\ mm.$  Dies ist ein hervorragend exakter römischer Fuß.

Belegbar tritt ein solches, 128/125 römische Fuß betragendes Grundmaß aber erst im 19. Jahrhundert als US-amerikanischer Typographenfuß in Erscheinung.

Die leichte Libra

Im Jahr 1920 behauptete Lucien Naville^[3] eine römische Libra von nur 322,56 Gramm, wobei er von einem Solidus (= 1/72 Libra) von genau 4,48 Gramm ausging. Rosati vertrat 1953 den gleichen Wert.^[4] Allerdings impliziert dieser Wert, die Römer hätten, um zu ihrem Pfund zu kommen, das ägyptisch-römische Talent von recht genau 26 Kilogramm zunächst durch 63 geteilt, dann nochmals durch 128, um dann schließlich das Ergebnis noch mit 100 zu multiplizieren. Beziehungsweise, was das gleiche Resultat ergibt: Talent durch 64  – das ist gleich das (spätere) Karlspfund –  durch 2, durch 63 [aber weshalb?], mal 100. Ein sehr umständlicher, somit wenig wahrscheinlicher Weg. Ein so niedriger Wert für die römische Libra wird auch sonst durch weiter nichts gestützt. Deshalb wird heute eine so leichte römische Libra auch von niemandem mehr vertreten.

Die mittlere Libra

Dennoch sind sich die heutigen historischen Metrologen weitgehend darin einig, dass der Böckhsche Wert wohl zu hoch ist. Schon Grierson schrieb 1960:
„Die meisten Nachschlagewerke unterstellen [weiterhin] die Richtigkeit des Wertes 327,45 Gramm für das römische Pfund. Dazu sind die Gelehrten gewöhnlich aus Bequemlichkeitsgründen (wörtlich: “for the sake of convenience”) bereit, obwohl sie gleichzeitig zugeben, dass dieser Wert wahrscheinlich zu hoch ist.“ ^[5]

Auch der 1963 in Ungarn gefundene Schatz von Szikáncs, der fast 1500 aus der Spätantike stammende, römische Solidi beinhaltet, stützt einen geringeren Wert als ca. 327½ Gramm.

Alle Werte zwischen etwa 323,2 und 326,4 Gramm, also im Intervall 324,8 ±1,6 Gramm können als mittlere römische Libra bezeichnet werden.

Bereits 1690 vertrat François Le Blanc^[6] einen solchen mittleren Wert. Auch Soetbeer, 1858^[7] und Guilhiermoz, 1906^[8] kamen zum selben Ergebnis. Alle drei gingen dabei allerdings von dem  – ihrer Meinung nach wohl idealen* –  Wert von genau 6144 französischen Grain aus, also von 6144 × (1/18,82715) gleich ca. 326,337 Gramm. In den letzten Jahrzehnten wurden vor allem drei weitere mittlere Werte vertreten: Genau 324 Gramm von Crawford (1974),^[9] mit dem expliziten Hinweis auf die gute Teilbarkeit dieser Zahl. Im Jahr 2004 hat der professionelle belgische Numismatiker Jean Elsen in einer wohldokumentierten Arbeit den Wert 326 Gramm vorgeschlagen.^[10] Bereits 1973 hatte Wolfgang Hahn den Wert 325 Gramm berechnet.^[11]

Der letztere, Hahnsche Wert erscheint angemessen, weil dieser Wert den Weg der einfachsten, vernünftigen Herleitung der griechischen Mine beschreitet. Die Griechen haben demnach das ägyptisch-römische Talent zu ziemlich genau 26 Kilogramm einfach durch 60 geteilt, um zu ihrer Mine zu kommen. Die römische Libra ist bekanntlich 12/16 der griechischen Mine.
Oder anders herum:  Aus dem Hahnschen Wert zu 325 Gramm ergibt sich:
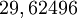
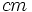
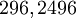
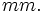$\sqrt[3] {325 * (4/3) * 60}$   $\ =$   $\ 29,62496$   $\ cm$   $\ =$   $\ 296,2496$   $\ mm.$  Auch dies ist zweifelsohne ein sehr guter römischer Fuß.

Die griechische Mine steht demnach zum Karlspfund im Verhältnis 60 : 64, bzw. 15 : 16; so wie die römische Libra mit dem Karlspfund die einfache Ratio 125 : 100, bzw. 5 : 4 unterhält.
Desgleichen beträgt die Ratio: Mine gegenüber der Kölner Mark 54 : 100, bzw. 27 : 50. Genau wie die Ratio zwischen Libra und Kölner Mark 72 : 100, bzw. gekürzt dann 18 : 25 beträgt.

Die obige Tabelle übernimmt prinzipiell den Hahnschen Wert. Da sich aber aus dem die Primzahl 13 enthaltenden, dezimal gerundeten Wert: 325 g, ein rechnerisches römisches Gran zu genau 47,01967592 Gramm ergibt, wurde der vereinfachte, 7-glatte Wert zu genau 47,04 mg für das römische Korngewicht bevorzugt. Wobei der eigentliche Hahnsche Wert nur 0,0432 % unter dem sieben-glatten liegt. Sieben-glatte Werte behaupten allerdings nicht, die römischen Metrologen hätten ihr Korngewicht auf ein Hundertstel Milligramm genau bestimmt, noch, dass die moderne historische Metrologie heute diesen Wert mit derselben Präzision feststellen könnte. Sieben-glatte Werte stellen nur eine praktische  – aber auch klar innerhalb des für das jeweilige Maß ermittelten Variationskoeffizienten liegende –  Over-all-Rundung aller, auch der abgeleiteten Maße dar.

 * In fine hatten Le Blanc, Soetbeer und Guilhiermoz gar nicht unrecht. Sie ignorierten dabei aber das französische Gewichtskomma von 3136 : 3125. Daher ihr nicht ganz korrekter Wert. (Cf. Karlspfund#Französische Ableitungen.)

Griechische vs. römische Drachme

Die griechische Drachme ist der 100. Teil der Mina; die römische der 96. Teil der Libra. So beträgt die Ratio zwischen römischer und griechischer Drachme genau 32 : 25.

Die Vielfachen der Unze

Alle einfachen Vielfache der römischen Unze haben eigene Namen.

1	Unze:	uncia
2	Unzen:	sextans	=   1/6 as
3	Unzen:	quadrans	=   1/4 as
4	Unzen:	trians	=   1/3 as
5	Unzen:	quincunx
6	Unzen:	semis	=   1/2 as
7	Unzen:	septunx
8	Unzen:	bes	=   2/3 as
9	Unzen:	dodrans	=   3/4 as
10	Unzen:	dextans	=   5/6 as
11	Unzen:	deunx
12	Unzen:	as	=   1 libra

Eineinhalb Unzen wurde bei den Römern sescuncia genannt.

Zeitrechnung

Siehe Hauptartikel: Julianischer Kalender

Der julianische Kalender mit einem Jahr (annum) von 365 ¼ Tagen (alle 4 Jahre ein Schaltjahr, ohne Ausnahme) wurde im Jahre 45 v. Chr. eingeführt.

Scriptores gromatici

Nach ihrem Instrument, der Groma, wurden die römischen Landvermesser Gromatici genannt. Ein lateinischer Text „Gromatici veteres“^[12] aus der Spätantike, wahrscheinlich aus dem fünften Jahrhundert nach Christus stammend, gibt die damaligen Maßverhältnisse wieder:

Lateinischer Text:

Digitus, uncia, palmus, Semipes, pes, gradus, Passus, decempeda, pertica, Actus, stadius, miliarius. Palmus habet digitos IIII, uncias III. Semipes habet palmos II. Pes habet palmos IIII. Cubitus habet pedem Iς. Gradus habet pedes IIς. Ulna habet pedes IIII. Passus habet pedes V. Decempeda pedes X digitorum XVI. Pertica habet pedes XII digitorum XVIII. Actus habet pedes CXX perticas X. Stadius habet pedes DCXXV. Miliarius habet pedes V. Porca habet pedes VII CC. Agnus habet pedes XIIII CCCC. Ingrus habet pedes XXVIII DCCC. Versus habet pedes VIII DCXL.

Dimidia sela, pars duodecima unciæ. Sela, secta pars unciæ. Lycus, quarta pars unciæ. Duo sela, tertia pars unciæ. Semiuncia, dimidia unciæ. Uncia unciæ. Sescuncia, uncia semis unciæ. Sextam, duae unciæ. Quadran, tres unciæ. Trian, quattuor unciæ. Quincum, quinque unciæ. Semis, sex unciæ. Septum, septem unciæ. Uem, octo unciæ. Dodran, novem unciæ. Dean, decem unciæ. Dabum, undecim unciæ. As, duodecim unciæ.

Deutsche Übersetzung:

Der Finger, das Zoll und die Handbreit, Der Halb-Fuß, der Fuß und der einfache Schritt, Der Doppelschritt, die Rute und die 12-Pygmen-Rute, Die Arpentlänge, das Stadion und die Meile. Die Handbreit misst 4 Finger oder 3 Zoll. Der Halb-Fuß misst 2 Handbreit. Der Fuß misst 4 Handbreit. Der Cubitus misst 1½ Fuß. Der einfache Schritt misst 2½ Fuß. Die Ulne misst 4 Fuß. Der Doppelschritt misst 5 Fuß. Die normale Rute misst 10 Fuß zu 16 Fingerbreit. Die 12-Pygmen-Rute misst 12 Fuß zu 18 Fingerbreit.    (Also: 12 Pygmen gleich 216 Fingerbreit) Die Arpentlänge misst 120 Fuß oder 10 normale Ruten. Das Stadion misst 625 Fuß. Die Meile misst 5 000 Fuß. Die Porca misst 7 200 Quadratfuß.    (Gleich zwei Stückchen Land oder ein halber Acker.) Der Acker misst 14 400 Quadratfuß. Das Joch misst 28 800 Quadratfuß. Der Versus misst 8 640 Quadratfuß.    (Gleich 60 Quadratruten oder 1⅔ Stückchen.)

Die Halb-Sela ist der zwölfte Teil der Unze.    (Gleich zwei Skrupel.) Die Sela ist der sechste Teil der Unze.    (Gleich vier Skrupel.) Der Lycus, die Viertel-Unze.    (Gleich zwei Siliqua.) Die Doppel-Sela, die Drittel-Unze.    (Gleich acht Skrupel.) Die Semiuncia, die Hälfte eine Unze. Die Unze. Die Sescuncia, eineinhalb Unzen. Der Sextans, zwei Unzen. Der Quadrans, drei Unzen. Der Trians, vier Unzen. Die Quincunx, fünf Unzen. Der Semis („ Halb-As “), sechs Unzen. Die Septunx, sieben Unzen. Der Bes, acht Unzen. Der Dodrans, neun Unzen. Der Dextans, zehn Unzen. Die Deunx, elf Unzen. Das As, zwölf Unzen.    (Anders gesagt ein Pfund.)

In diesem Text aus der Spätantike, auf der Schwelle zum Mittelalter, sind kleinere Unterschiede im Gebrauch der Maße und Gewichte im Vergleich zur klassischen Zeit festzustellen. Die genannten Grundmaße aber  – sowohl in fast allen Namensgebungen, als auch in ihren Verhältnissen zu den anderen Maßen –  sind jedoch gleich geblieben.

Literatur

• Oswald Ashton Wentworth Dilke: Mathematik, Maße und Gewichte in der Antike. RUB 8687. Reclam, Stuttgart 1991, ISBN 3-15-008687-6
• Friedrich Hultsch: Griechische und römische Metrologie. 2. Aufl. Weidmann, Berlin 1882. Nachdruck: Akademische Druck- und Verlags-Anstalt, Graz 1971

Weblinks

• Vormetrische Längeneinheiten - Seite von Rolf C. A. Rottländer

Einzelnachweise

1. ↑ August Böckh: Metrologische Untersuchungen über Gewichte, Münzfusse und Masse des Altertums. Berlin 1838. S. 165.
2. ↑ Theodor Mommsen: Römische Geschichte. Erstes Buch, Dritter Absatz: „… der heutige Silberwert des entsprechenden Gewichtsquantums zugrunde gelegt wurde, wobei das römische Pfund (= 327,45 Gramm) Geld gleich 4000 Sesterzen …“ [1]
3. ↑ Lucien Naville: Fragments de métrologie antique. In: Revue suisse de numismatique. 22 (1920) S. 42–60, 257–263
4. ↑ F. Panvini Rosati: Ripostiglio di aurei tardo-imperiali a Comiso. In: Accademia degli Lincei, Rendiconti morali, série 8, S. 422–440
5. ↑ Philipp Grierson: The monetary reforms of ‘Abd al-Malik. In: Journal of the Economic and Social History of the Orient 3 (1960). S. 252: „… since calculations based on the Roman pound in most works of reference assume the correctness of 327.45 g., scholars have usually been prepared to retain it for the sake of convenience while admitting that it is probably too high.“
6. ↑ François le Blanc: Traité historique des monnoyes de France. Paris 1690.
7. ↑ Adolf Soetbeer: Über die Münz- und Gewichts-Verhältnisse unter den Merovingern und Karolingern, sowie über den Ursprung und die Verbreitung des Mark-Gewichts. Hamburg 1858
8. ↑ Paul Guilhiermoz: Notes sur les poids du moyen âge. Bibliothèque de l’Ecole des chartes 67 (1906), S. 161–233, 402–450.
9. ↑ Michael Hewson Crawford: Roman Republican Coinage. 2 Bde. Cambridge 1974.
10. ↑ Jean Elsen: Le système pondéral romano-byzantin (fin 3e siècle – fin 8e siècle). 2004 [2]
11. ↑ Wolfgang Hahn: Moneta Imperii Byzantini. Bd. 1: Von Anastasius I. bis Justinianus I (491–565). Österreichische Akademie der Wissenschaften, Wien 1973, ISBN 3-7001-0005-1
12. ↑ Friedrich Bluhme, Karl Lachmann, Theodor Mommsen, Andreas Rudorff (Hrsg.): Gromatici veteres. Die Schriften der römischen Feldmesser. Berlin 1848