- Linearisierung
-
Bei der Linearisierung wird eine nichtlineare Funktion oder Differentialgleichung durch eine lineare Funktion oder Differentialgleichungen angenähert. Sie wird angewandt, da lineare Funktionen oder lineare Differentialgleichungen sehr einfach berechnet werden können und die Theorie im Gegensatz zu nichtlinearen Systemen sehr gut ausgebaut ist.
Inhaltsverzeichnis
Anwendungen
Anwendung findet die Linearisierung unter anderem in der Elektrotechnik und der Regelungstechnik zur Umwandlung nichtlinearer Systeme in lineare Systeme.
Das Ergebnis der Netzwerkanalyse ist unter Umständen ein nichtlineares Gleichungssystem, welches in ein lineares Gleichungssystem überführt werden kann. Bei dynamischen Systemen ist eine Analyse auf der Grundlage linearer Differenzialgleichungen leichter möglich.
Tangente
Das einfachste Verfahren zur Linearisierung ist das Einzeichnen der Tangente in den Graphen. Daraufhin können die Parameter der Tangente abgelesen werden, und die resultierende lineare Funktion (Punkt-Richtungs-Gleichung der Geraden)
approximiert die Originalfunktion um den Punkt
 . Dabei ist
. Dabei ist  der Anstieg im Punkt
der Anstieg im Punkt  .
.Wenn die Funktion in analytischer Form vorliegt, kann die Gleichung der Tangente direkt angegeben werden.
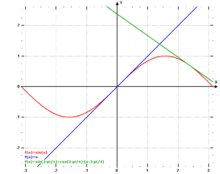
Der relative Fehler der Approximation ist
Für die Funktion
 gilt:
gilt:Multiplikation
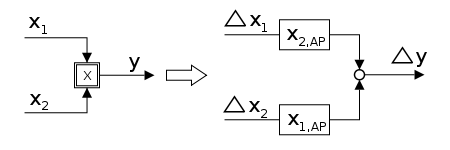
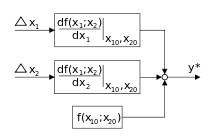
Befindet sich im Signalflussplan eine Multiplikationsstelle lässt sich diese durch Linearisierung in eine Additionsstelle umwandeln. Das der Umwandlung zugrundeliegende Konzept erläutert die nachfolgende Rechnung.
Linearisierung einer Multiplikation im Arbeitspunkt (AP):
Multiplikation durch Addition genähert:

- Fehler:

Beispiel:

- Wähle:


- Fehler:

Division
Es gilt
und
oder
Für die Geometrische Reihe gilt
 .
.
Mit
 und
und  gilt
gilt .
.
Damit ist die linearisierte Division
Linearisieren gewöhnlicher Differentialgleichungen
Das bekannteste Beispiel für die Linearisierung einer nichtlinearen Differenzialgleichung ist das Pendel. Die Gleichung lautet:
Der nichtlineare Teil ist
 . Die Tangente daran ist
. Die Tangente daran istMit dem Arbeitspunkt
 gilt für kleine
gilt für kleine 
 und damit die linearisierte Differenzialgleichung
und damit die linearisierte Differenzialgleichung .
.
Weitere Details sind in Zustandsraumdarstellung beschrieben.
Tangentialebene
Soll eine gegebene Funktion
 in einem Punkt
in einem Punkt  linearisiert werden, wird sich der Taylor-Formel bedient. Das Ergebnis entspricht der Tangentialebene in diesem Punkt.
linearisiert werden, wird sich der Taylor-Formel bedient. Das Ergebnis entspricht der Tangentialebene in diesem Punkt.Für die Funktion
 gilt in der Umgebung des Punktes x10,x20:
gilt in der Umgebung des Punktes x10,x20:Beispiel:
ergibt die Tangentialebene
Siehe auch
- Taylor-Reihe
- Taylor-Formel
- Linearität
- Linearisierung von resistiven Sensoren (Elektrotechnik)
- Methode der globalen Linearisierung
Weblinks
- Skript der TU Wien
- Skript der ETH Zürich
Wikimedia Foundation.

 ,
,