Hauptkrümmung

Hauptkrümmung ist ein Begriff aus der Differentialgeometrie. Jedem Punkt einer gegebenen Fläche im dreidimensionalen Raum ($\mathbb{R}^3$) werden zwei Hauptkrümmungen zugeordnet.

Definition

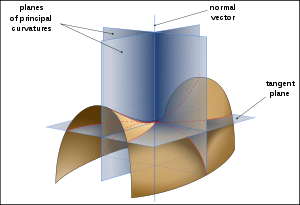
Gegeben sei ein Punkt einer regulären Fläche im $\mathbb{R}^3$. Jeder Tangentialrichtung, also jeder Richtung, die ein Tangentialvektor in diesem Punkt annehmen kann, wird die Normalkrümmung zugeordnet: Man versteht darunter die Krümmung der ebenen Kurve, die sich durch Schnitt der gegebenen Fläche mit der durch den Flächennormalenvektor und die gegebene Tangentialrichtung bestimmten Ebene ergibt. Den Minimalwert und den Maximalwert dieser Krümmungen bezeichnet man als die beiden Hauptkrümmungen k₁ und k₂.

Beispiele

• Bei einer Kugel mit Radius r stimmen in jedem Punkt die beiden Hauptkrümmungen überein: k₁ = k₂ = 1 / r

• Gegeben sei die gekrümmte Fläche eines geraden Kreiszylinders mit Grundkreisradius r. In diesem Fall haben die Hauptkrümmungen in einem beliebigen Punkt der Fläche die Werte 0 (Tangentialrichtung parallel zur Achse des Zylinders) und 1 / r (Tangentialrichtung senkrecht zur Achse des Zylinders).

Dasselbe gilt für die Kegel sowie für die abwickelbaren Flächen (oder Torsen). Dabei ist eine Torse (falls sie kein Kegel oder Zylinder ist) die von den Tangenten einer Raumkurve gebildete Fläche.

• Gegeben sei ein Ellipsoid mit den Halbachsen a, b und c. In den Endpunkten (Scheitelpunkten) der Halbachse a sind die Hauptkrümmungen gleich a / b² und a / c².

Sattelfläche mit den Normalenebenen in Richtung der Hauptkrümmungen

Eigenschaften

• Die beiden Hauptkrümmungen sind die Eigenwerte der Weingartenabbildung.

• Die zu den beiden Hauptkrümmungen gehörigen Tangentialrichtungen sind zueinander senkrecht.

• Die gaußsche Krümmung K ist das Produkt der Hauptkrümmungen: K = k₁k₂

• Die mittlere Krümmung H ist das arithmetische Mittel der Hauptkrümmungen: $H = \tfrac{1}{2} (k_1 + k_2)$

• Sind die gaußsche Krümmung K und die mittlere Krümmung H bekannt, so ergeben sich die Hauptkrümmungen als Lösungen der folgenden quadratischen Gleichung: $k^2 - 2 H k + K \, = \, 0$

• Für eine beliebige Tangentialrichtung lässt sich die Normalkrümmung k_n durch die beiden Hauptkrümmungen ausdrücken:

$k_n \, = \, k_1 \cos^2 \epsilon + k_2 \sin^2 \epsilon$ (Satz von Euler)

Dabei steht $\epsilon$ für den Winkel zwischen der gegebenen Tangentialrichtung und der zu k₁ gehörigen Tangentialrichtung.

Literatur

• Manfredo Perdigão do Carmo: Differential Geometry of Curves and Surfaces, Prentice-Hall, Inc., New Jersey, 1976, ISBN 0-13-212589-7