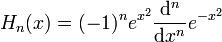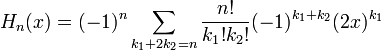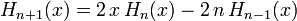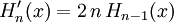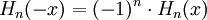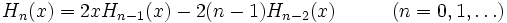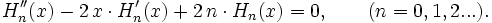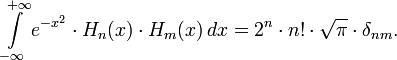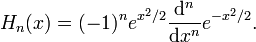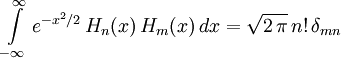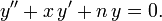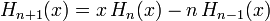- Hermitesche Differentialgleichung
-
Die hermiteschen Polynome (nach Charles Hermite) sind Polynome mit folgenden äquivalenten Darstellungen:
bzw.
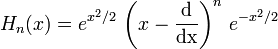
Inhaltsverzeichnis
Explizite Darstellung
Aus der ersten Darstellung erhält man mit der Formel von Faà di Bruno die explizite Darstellung
also
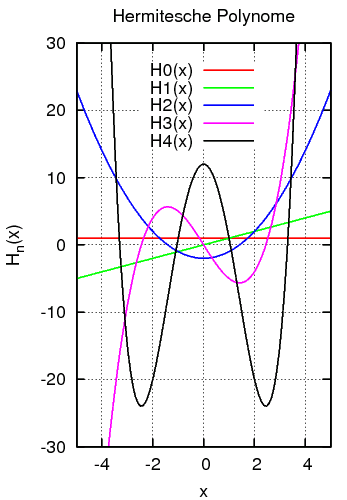
- H0(x) = 1
- H1(x) = 2x
- H2(x) = (2x)2 − 2 = 4x2 − 2
- H3(x) = (2x)3 − 6(2x) = 8x3 − 12x
- H4(x) = (2x)4 − 12(2x)2 + 12 = 16x4 − 48x2 + 12
Hermitesche Polynome lassen sich durch folgende Rekursionsformeln berechnen:
Da bei jedem Iterationsschritt ein x hinzumultipliziert wird, sieht man schnell, dass Hn(x) ein Polynom von Grade n ist. Der Koeffizient der höchsten Potenz xn ist 2n. Für gerade n treten ausschließlich gerade Potenzen von x auf, entsprechend für ungerade n nur ungerade Potenzen, was sich mathematisch durch die Identität
ausdrücken lässt.
Die rekursive Darstellung der o.g. Hermiteschen Polynome lässt sich durch die einfache Substitution n' = n + 1 auch wie folgt schreiben:Mit Hilfe der bekannten Anfangsbedingungen H0(x) = 1 und H1(x) = 2x lassen sich die Funktionswerte mit folgender rekursiver Pascal-Funktion leicht berechnen:
Function Hermite(n:Byte;x:Extended):Extended; Begin If n=0 Then Hermite:=1 Else If n=1 Then Hermite:=2*x Else Hermite:=2*x*Hermite(n-1,x)-2*(n-1)*Hermite(n-2,x) End;
Die allgemeinere Ableitungsformel
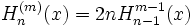 lässt sich wie folgt umsetzen:
lässt sich wie folgt umsetzen:Function HermiteAbleitung(n,m:Byte;x:Extended):Extended; Begin If m=0 Then HermiteAbleitung:=Hermite(n,x) Else If n<m Then HermiteAbleitung:=0 Else If m=1 Then HermiteAbleitung:=2*n*Hermite(n-1,x) Else HermiteAbleitung:=2*n*HermiteAbleitung(n-1,m-1,x) End;
Die hermiteschen Polynome (mit einem festen n) sind die Lösungen einer linearen Differentialgleichung zweiter Ordnung:Orthogonalität
Die hermiteschen Polynome erfüllen bezüglich der Gewichtsfunktion
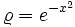 die Orthogonalitätsrelation
die OrthogonalitätsrelationDas heißt, dass bestimmte reelle Funktionen nach den hermiteschen Polynomen in eine Reihe entwickelt werden können.
Andere Darstellung der hermiteschen Polynome
Eine andere Definitionsmöglichkeit der hermiteschen Polynome ist
Sie sind bezüglich der Gewichtsfunktion
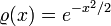 orthogonal
orthogonalund erfüllen die Differentialgleichung
Sie lassen sich rekursiv durch
bestimmen.
Anwendung
Ihre Bedeutung erhalten die Hermite-Polynome durch ihre vielseitige Anwendbarkeit in der Physik. Zum Beispiel werden sie zur Konstruktion der orthonormierten Lösungsfunktionen des quantenmechanischen harmonischen Oszillators benötigt. Diese entsprechen den hermiteschen Funktionen, die man durch Multiplikation mit der gaußschen Normalverteilung und geeigneter Normierung erhält.
Eine weitere Anwendung finden Sie in der Finite-Elemente-Methode als Formfunktionen.
Siehe auch
Literatur
- I.N. Bronstein u.A.: Taschenbuch der Mathematik 5. Aufl. Verlag Harri Deutsch, Frankfurt am Main, Thun, 2001 ISBN 3-8171-2005-2
- Milton Abramowitz und Irene Stegun: Pocketbook of Mathematical Functions
- Murray R. Spiegel, Höhere Mathematik für Ingenieure und Naturwissenschaftler McGraw-Hill
- Eric W. Weisstein. „Hermite Polynomial.“ From MathWorld -A Wolfram Web Resource. http://mathworld.wolfram.com/HermitePolynomial.html
- Skript des Schülerforschungszentrum Bad Saulgau [1]
Wikimedia Foundation.