Hundekurve

Der Name Hundekurve beschreibt als Trivialname verschiedene ebene Kurven. Der Ausdruck leitet sich ab von dem Weg, den ein idealisierter Hund beschreibt. Die Untersuchung der sogenannten Hundekurven ist ein Teilgebiet der Verfolgungsprobleme.

Varianten

Der Weg des Hundeführers sei im Folgenden eine Gerade:

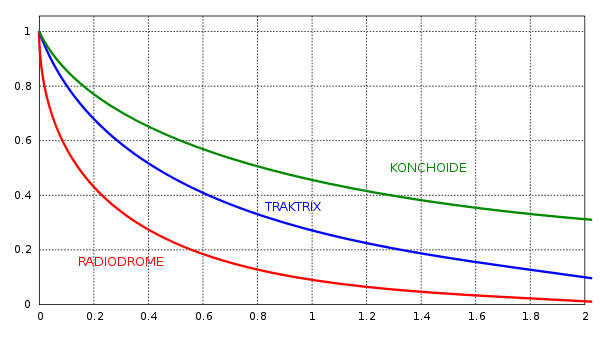
• Hund und Baum: Es gebe einen fiktiven Baum, der nicht auf dem Weg des Hundeführers stehe, sondern mindestens eine Leinenlänge entfernt sei. Versucht nun der Hund, die Entfernung zwischen sich und dem Baum minimal zu halten, so entsteht eine Konchoide von Nikomedes.

• Hund an der Leine: Befindet sich der Hund nicht auf dem Weg des Hundeführers, und wird er an der Leine gezogen, wobei er versucht, seine Geschwindigkeit zu minimieren, entsteht eine eigentliche Traktrix.

• Hund verfolgt Fußgänger: Befindet sich der Hund nicht auf dem Weg des Hundeführers, und läuft er immer mit einer gewissen Geschwindigkeit auf die augenblickliche Position seines Hundeführers zu, während dieses sich weiterbewegt, entsteht eine gerade Radiodrome. Je nach Geschwindigkeitsverhältnis erreicht der Hund sein Herrchen, oder nicht.

Vergleich zwischen verschiedenen Hundekurven. Die jeweiligen relevanten Parameter sind 1

Luftfahrt

Hundekurve beim Anflug auf ein NDB bei Seitenwind

→ Hauptartikel: Homing (Luftfahrt)

In der Fliegerei kann aufgrund von Seitenwindeinfluss beim sogenannten Homing der Flugweg einer Hundekurve entsprechen: Ohne Windeinfluss beschreibt der Flugweg zwischen zwei Punkten eine Gerade. Bei Seitenwind wird das Flugzeug jedoch von seinem eigentlichen Flugweg abgetrieben. Korrigiert der Pilot die Ausrichtung der Flugzeugnase direkt auf das Ziel kontinuierlich, resultiert als Kurslinie über Grund keine Gerade sondern eine immer enger werdende Kurve (Radiodrome).

Hockey

Ebenfalls bezeichnet der Begriff Hundekurve einen bestimmten Laufweg beim Hockey. Hierbei startet der Spieler zuerst geradeaus (am rechten Spielfeldrand), um dann nach innen zu ziehen (Richtung Tor und parallel zur Grundlinie). Das Pendant auf der linken Spielfeldhälfte heißt "Katzenkurve", wobei dieser Begriff nicht sehr populär ist.

Motorsport

Der Begriff Hundekurve wird weiterhin von Motorsportlern verwendet, um sich progressiv zuziehende Straßenkurven zu beschreiben (siehe auch obige Grafik); das heißt der Radius wird im Laufe der Kurve geringer. Diese Art von Kurve ist im normalen Straßenverkehr besonders für ungeübte Fahrer gefährlich, da sie nur schwer vorherzusehen ist (sie tritt abseits von Rennstrecken zumeist an Berghängen auf) und während der Kurvenfahrt eine schnelle Korrektur des Lenkeinschlages und evtl. der Geschwindigkeit erfordert. Beim Motorradfahren ist auch eine Verstärkung der Schräglage erforderlich. Da in den meisten Fällen die Technik mehr Schräglage gestatten würde, wäre dies eigentlich kein Problem. Gerade ungeübte Fahrer erreichen jedoch leicht die Angstschwelle (vor größeren Schräglagen) und bremsen, was – je nach Fahrwerksgeometrie und -abstimmung – ein mehr oder weniger starkes Aufrichten des Motorrades zur Folge hat. Dadurch vergrößert sich der gefahrene Radius, während sich der echte Radius verringert. Es besteht also die Gefahr, dass dem Fahrer „die Straße ausgeht“. Bereits die Lastwechselreaktionen beim Gaswegnehmen können den Fahrer in Bedrängnis bringen.

Weblinks

• Verfolgungsprobleme - ein historischer Überblick
• Verfolgungsprobleme – Interessante Java-Applets