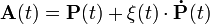- Verfolgerkurve
-
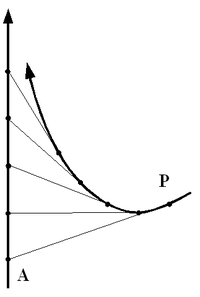
Die Radiodrome („Leitstrahlkurve“, v. lat. radius „Strahl“ und griech. dromos „Lauf, Rennen“), oder Verfolgungskurve ist eine spezielle ebene Kurve. Sie beschreibt die Bewegung eines Punktes, der einen anderen Punkt verfolgt. Beide Punkte bewegen sich dabei mit konstanter, aber nicht notwendigerweise gleicher Geschwindigkeit.
Die gerade Radiodrome beschreibt den einfachen Fall, in dem der Verfolgte sich auf einer Gerade bewegt. Pierre Bouguer beschrieb sie 1732 erstmals. Sie ist eine der Kurven, die mit dem Trivialnamen Hundekurve bezeichnet werden, nach einer Formulierung der Fragestellung mit einem Hund, der seinen Herrn verfolgt. Pierre-Louis Moreau de Maupertuis erweiterte die Problematik schon bald darauf auf beliebige Leitkurven. Dies führte zur Definition der allgemeinen Radiodrome.
Die Kurve tritt typischerweise in Tracking-Problemen in der Robotik und dynamischen Simulationen auf (Verfolgungsprobleme).
Inhaltsverzeichnis
Gerade Radiodrome
- Bildungsgesetz
- Sei A0 der Startpunkt eines „Verfolgten“ , und P0 der Startpunkt eines „Verfolgers“.
- Wandert der Punkt A mit der Geschwindigkeit v = const. auf einer Geraden, und bewegt sich der Punkt P mit der Geschwindigkeit w = const. immer in Richtung des Punktes A, dann durchläuft P eine Radiodrome.
- Sei weiters das Geschwindigkeitsverhältnis k = v / w.
- Funktionsgleichung in Kartesischen Koordinaten
- A0(0|0) im Ursprung, P0(1|0) auf der x-Achse, A bewegt sich entlang der y-Achse:
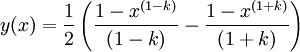 (k ≠ 1)
(k ≠ 1)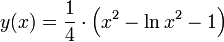 (k = 1)
(k = 1)- Den zweiten Fall nennt man eigentliche Radiodrome. Sie stellt den einfachsten Spezialfall dar.
Herleitung
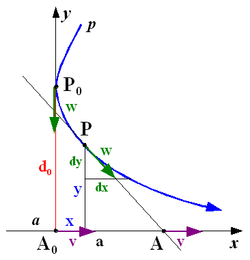
Im folgenden sei die 1. Hauptlage betrachtet: A0(0|0), P0(0|1), A wandert entlang der x-Achse, k > 0:
- Die Tangentenbedingung
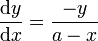 ergibt die Differentialgleichung: y + y'(a − x) = 0 mit y > 0
ergibt die Differentialgleichung: y + y'(a − x) = 0 mit y > 0 - Mit a = vt folgt
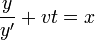 , mit Differentiation nach x:
, mit Differentiation nach x: 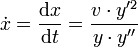
- Hierbei ist die Bogenlänge
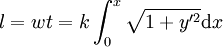
- aus dx2 + dy2 = w2dt2 folgt
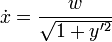
- Nach Gleichsetzen ergibt sich die Differentialgleichung in y:
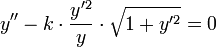
- Die Lösung gelingt mit Substitution
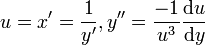 , durch Trennen der Variablen zu
, durch Trennen der Variablen zu 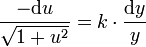 ,
,
durch Integrieren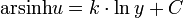 (siehe arsinh), sowie Rücksubstitution und Anwenden der Definitionsformel des sinh x, mit C1 = eC, zu:
(siehe arsinh), sowie Rücksubstitution und Anwenden der Definitionsformel des sinh x, mit C1 = eC, zu: ![x' = \frac{\mathrm{d}x} {\mathrm{d}y} = \frac{1}{2} \left[ C_1 \cdot y^{-k} - \frac{1}{C_1} \cdot y^{k} \right]](/pictures/dewiki/50/23eb43eb69659e36bbbd9b0d25461df8.png)
- Hierauf erneutes Integrieren, unter Berücksichtigung von C2
- Aus den Randbedingungen dx/dy|y=1 = 0 folgt C1 = 1, und x|y=1 = 0 folgt C2 = k/(1-k²) bzw. -¼, also:
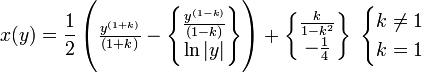
- Oder, da für den interessanteren Fall (Hauptast) gilt: y < 1, ist der 2.Term immer positiv, mit k1 = 1-k, k2 = 1+k:
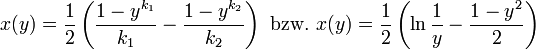
Eine explizite Darstellung nach y(x) ist hierbei nicht möglich.
E. W. Weisstein gibt in (3) eine geschlossene Parameterdarstellung.
- Allgemeine Lage
- Für einen beliebigen Abstand d0 = A0P0 ≠ 0 ersetzt man x → x/d0, y → y/d0 (normierte Variablen).
- Ist die Startrichtung nicht normal auf der Leitgeraden, so erhält man andere Randbedingungen. Der Umkehrpunkt errechnet sich aus x' = 0, d0 = y|x'=0.
- Für eine allgemeine Lage der Leitgerade ist eine geeignete Koordinatentransformation vorzunehmen.
Eigenschaften
- Die Verbindungslinie von entsprechenden A und B ist Tangente an die Radiodrome.
- Offensichtlich ist x > 0 für alle y : Der Startpunkt des Verfolgers ist der Umkehrpunkt der Kurve (bezüglich der x-Achse).
- Der Nebenast, also y > d0 ( t → -∞ ) divergiert immer, und zwar ohne Asymptote.
- Die Nullstelle ist gegeben durch den Term k / (1-k²).
Analyse des Geschwindigkeitsparameters k
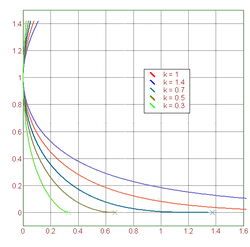
k >= 1: Die Nullstelle liegt augenscheinlich außerhalb des Definitionsbereiches. Folglich nähert sich die Kurve asymptotisch der x-Achse: Der Verfolger ist langsamer und erreicht den Verfolgten nicht, noch kreuzt er seine Bahn.
- Bei gleicher Geschwindigkeit (k = 1) läuft der Verfolger in zunehmend gleichem Abstand hinter dem Verfolgten her: Die Kurve zeigt das Grenzwert-Verhalten einer Traktrix.
k < 1: Es gibt es genau eine Nullstelle. Der Verfolger ist schneller als der Verfolgte, und erreicht jenen in endlicher Zeit. Wir nennen die Nullstelle Treffpunkt oder Fangpunkt, die Kurve ist im Fangpunkt tatsächlich zu Ende.
- Für k >= ½ konvergiert die Krümmung gegen 0, der Verfolger erreicht sein Opfer genau von hinten.
- Für k = ½ konvergiert die Krümmung allgemein gegen d0/2.
- Für k < ½ schneidet im Treffpunkt die Tangente der Radiodrome die x-Achse unter einem Winkel ≠ 0, der Verfolger erreicht sein Ziel also von der Seite.
Ist k < 0 (also w vom Verfolgten weg orientiert, oder A wandert in Richtung negativer x-Werte) liegt der Graph spiegelverkehrt zur y-Achse.
Der Fall k = 0 ist trivial, nämlich eine Gerade. Der Verfolger ist „unendlich“ schnell, oder der Verfolgte steht still.
Für rationales k degeneriert die Funktion zu einer algebraischen Kurve.
Allgemeine Radiodrome
Der Begriff der Radiodrome lässt sich verallgemeinern:
- Sei A0 ein Punkt einer Kurve a, und P0 ein beliebiger Punkt, t eine reelle Zahl im Sinne eines Zeitparameters. Sei d0 der Abstand A0P0.
- Nun wandert der Punkt A(t) mit A(0) = A0 für wachsendes t mit der Geschwindigkeit v(t) = |A˙| entlang der Kurve a, und der Punkt P(t) “verfolgt“ ihn mit P(0) = P0 mit der Geschwindigkeit w(t) = |P˙|.
- Die Menge aller Punkte, die P(t) durchläuft, sei die Kurve p. Man bezeichnet diese als Radiodrome der Kurve a.
- mit
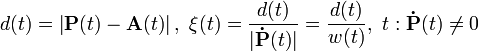
- oder
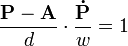 ..Tangentenbedingung
..Tangentenbedingung
Die allgemeine Radiodrome gehört als Spezialfall zur Klasse der Schielwinkelkurven.
Siehe auch
Weblinks
- Simulation einer Verfolgung mit Java und Verfolgungsprobleme, Menü: Hundekurven – Verschiedene Java-Applets
- Hundekurven – detaillierte Herleitung
- Pursuit Curve -- From MathWorld – Literaturangaben (englisch)
Wikimedia Foundation.