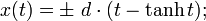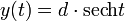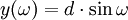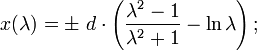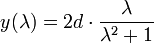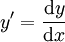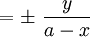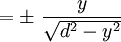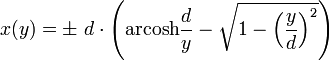Fahrstreifenverbreiterung

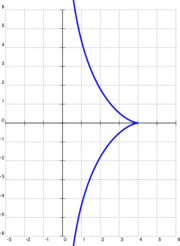
Traktrix (v. lat. trahere „schleifen, schleppen“), auch Schleppkurve, Ziehkurve, Zugkurve, Treidelkurve, ist eine spezielle ebene Kurve. Der Name erklärt sich daraus, dass diese Kurve von einem Massenpunkt beschrieben wird, der an einer Stange gezogen wird.

Eigentliche Traktrix, Funktionsgraph für x und y, P startet in (4,0)

Die Eigentliche (Gerade) Traktrix ist die Kurve, bei der für jede Tangente der Abschnitt zwischen dem Berührpunkt und der Koordinatenachse konstant ist. Man nennt sie auch Huygens-Traktrix, nach Christiaan Huygens, der das zugrundeliegende Problem 1693 löste, nachdem es von Claude Perrault beschrieben wurde. Sie ist eine der Kurven, die mit dem Trivialnamen Hundekurve bezeichnet werden. Diese Kurve spielt in der hyperbolischen Geometrie eine wichtige Rolle.

Schon Leonhard Euler und andere beschäftigten sich bald darauf mit der Allgemeinen Traktrix, die beliebige Leitkurven erlaubt. Sie spielt eine wichtige Rolle in der Modellierung des Fahrverhaltens, nämlich der Rückwärtsfahrt und dem Verhalten beim Durchfahren einer Kurve.

Eigentliche Traktrix

Bildungsgesetz

Sei A₀ der Startpunkt eines „Ziehenden“, und P₀ der Startpunkt eines „Gezogenen“ sowie d der Abstand A₀P₀ > 0.

Wandert der Punkt A auf einer Geraden, und “folgt“ ihm der Punkt P in konstantem Abstand d, dann durchläuft P eine Traktrix.

Funktionsgleichung in Kartesischen Koordinaten

A₀(0|0) im Ursprung, P₀(d|0) auf der x-Achse, A bewegt sich entlang der y-Achse:

$y(x) = \pm\ d \cdot \underbrace{\ln \left| {d +\sqrt{d^2-x^2} \over x} \right|}_{=\operatorname{arcosh} \frac dx} \mp \sqrt{d^2-x^2}$

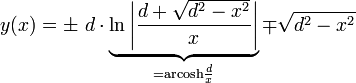
Eine explizite Darstellung nach x(y) ist hierbei nicht möglich.

Parameterdarstellungen

• mit t = arcosh d/y ergibt sich eine elegante Form (mit sech z = 1/cosh z):

$x(t) = \pm\ d \cdot ( t - \tanh t );$   $\quad y(t) = d \cdot \operatorname{sech} t$

• mit ω, sin ω = y/d, 0 ≤ ω ≤ π/2 , dem Winkel zwischen x-Achse und Tangente – erfordert keine Hyperbelfunktion:

$x(\omega) = \pm\ d \cdot \left( \cos \omega + \ln \tan {\omega \over 2} \right);$   $y(\omega) = d \cdot \sin \omega$

• mit λ = tan ω/2, eine Darstellung, die die Arbeit mit tabellierten Werten erleichtert:

$x(\lambda) = \pm\ d \cdot \left( {{\lambda^2 -1} \over {\lambda^2 +1}} - \ln \lambda \right);$   $y(\lambda) = 2d \cdot {{\lambda} \over {\lambda^2 +1}}$

Herleitung

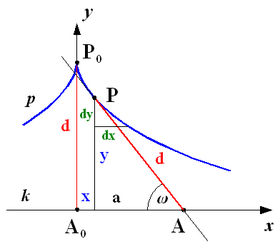
Im folgenden sei die Kurve in 1. Hauptlage betrachtet: A₀(0|0), P₀(0|d), A wandert entlang der x-Achse, mit a = AA₀:

1. Mit d² = (a-x)² + y² lässt sich aus dem Bildungsgesetz direkt folgende Differentialgleichung (Tangentenbedingung) ablesen:

   $y' = {\mathrm d y \over \mathrm d x}$$= \pm\ {y \over {a -x}}$$= \pm\ {y \over {\sqrt {d^2-y^2} }}$

2. Die Lösung gelingt mit der Substitution d/y = cosh t. Dies entspricht der oben erwähnten Parameterdarstellung: y = d / cosh t.
3. Es folgt dy = - d·sinh t / cosh² t·dt und dann durch Trennung der Variablen 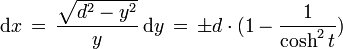${\mathrm d}x \,=\, \frac{\sqrt{d^2-y^2}}{y}\,{\mathrm d}y \,=\, \pm d \cdot (1-\frac{1}{\cosh^2t})$. Integration liefert x = ± d·(t – tanh t) und Rücksubstitution:

   $x(y) = \pm\ d \cdot \left( \operatorname{arcosh} {d \over y} -\sqrt{1-\left( {y \over d} \right)^2} \right)$

Eigenschaften

• Offensichtlich ist 0 < |y| ≤ |d|. Ist d < 0 liegt der Graph spiegelverkehrt zur y-Achse.
• Für P₀(0|d) fallen beide möglichen Tangenten mit der y-Achse zusammen, der Punkt P₀ ist also eine eigentliche Spitze.
• Die Länge der Kurve zwischen x=x₁ und x=x₂ errechnet sich zu: $l = d \cdot \ln \left( {x_1 \over x_2} \right)$
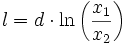
• Die Fläche unter der Traktrix: $A = d^2 \cdot \tfrac{\pi}{2}$
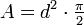
• Die Evolute der Traktrix ist die Katenoide $x = d \cdot \operatorname{cosh} \left( {y \over d} \right)$
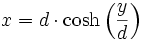
• Wird diese Kurve um die x-Achse rotiert, so entsteht die Pseudosphäre, welche in der hyperbolischen Geometrie die Rolle der Kugel einnimmt. So ist etwa die Fläche unter der Traktrix dieselbe wie beim Halbkreis. Die Traktrix ist hierbei als Geodäte die Entsprechung der Geraden im „normalen“ (euklidischen) Raum.

Allgemeine Traktrix

Der Begriff der Traktrix lässt sich verallgemeinern:

Gegeben seien ein Parameter t, eine Kurve k (die Leitkurve), ein beliebiger Punkt A₀ (Startpunkt), der auf der Kurve k liegt, und ein beliebiger Punkt P₀. Sei d der Abstand A₀P₀.

Wandert der Punkt A(t) mit A(0) = A₀ mit wachsendem t nun entlang der Kurve k, so „folgt“ ihm der Punkt P(t) mit P(0) = P₀ in konstantem Abstand d.

Die Menge aller Punkte, die P(t) durchläuft, bezeichnet man als die Traktrix der Kurve k.

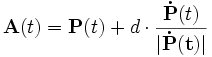$\bold A(t) = {\bold P(t)} +d \cdot \frac{ {\bold {\dot P}(t)} }{ {| {\bold {\dot P(t)}} |} }$ mit $t: {\bold{\dot P}(t)} \neq 0$

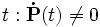
Die Traktrix ist also eine allgemeine Radiodrome mit der Funktion $\xi (t) = \frac{d}{ {| {\bold{\dot P}(t)} |}}$

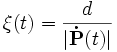
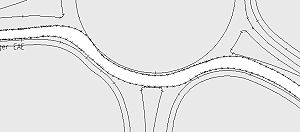
Anwendung im Straßenbau

Die weiße Fläche stellt die Schleppkurve eines Pkws bei der Befahrung eines Kreisverkehrs dar.

Mit Hilfe der Schleppkurve kann das Fahrverhalten von Fahrzeugen modelliert werden, insbesondere der benötigte Platz bei Kurvenfahrten, aber auch das Verhalten bei Rückwärts-Fahrten sowie beim Abschleppen eines zweiten Fahrzeugs.

Beim Lenkvorgang eines Fahrzeuges laufen die Achsen hinter der Lenkachse „aus der Spur“: Sie verfolgen nicht exakt denselben Weg, so dass für eine Kurvenfahrt eine größere Fläche überstrichen wird, als der Spurstand vorgibt. Die überstrichene Fläche lässt sich mit Hilfe von Schleppkurven von Bemessungsfahrzeugen ermitteln.

Die Größe und Art der überstrichenen Fläche hängt von mehreren Faktoren ab:

• Dem Kurvenradius: Je enger eine Kurve gefahren wird, desto breiter ist die überstrichene Fläche.
• Der Länge des Fahrzeuges: Je länger ein Fahrzeug ist, desto größer ist die überstrichene Fläche.
• Der Lage der Achsen: Je nachdem, wo die Achsen im Verhältnis zur Fahrzeuglänge liegen, wird entweder eine größere Fläche zur Kurveninnenseite oder zur Kurvenaußenseite überstrichen (Warnhinweis "Heck schwenkt aus").
• Der Gliederung des Fahrzeuges: Anhänger, Sattelaufleger, etc.
• Der Anzahl der gelenkten oder drehbaren Achsen.

Für die Bemessungsfahrzeuge gibt es vorgefertigte Schleppkurven, für Spezialfahrzeuge können mit Hilfe von Computersimulationen die Schleppkurven berechnet werden.

Die überstrichenen Flächen sind freizuhalten, z. B. von Lichtsignalanlagen, Schildern etc. Die befestigten Verkehrsflächen sind entsprechend den maßgebenden Schleppkurven auszubilden. Dafür werden beispielsweise bei engen Radien Fahrstreifenverbreiterungen notwendig.

Bei der Ausbildung von Kurven und Kreuzungen ist darauf zu achten, dass der Gegenverkehr nicht behindert und gefährdet wird.

Weblinks

• Verfolgungsprobleme, Menü: Schleppkurven – Java-Applets
• Johanneum Lüneburg Kurven Traktrix – Artikel für Schüler
• Tractrix -- From MathWorld – (englisch), weitere Literaturangaben.
• Lexikon der Unfallrekonstruktion