- Integralkern
-
Eine Gleichung wird in der Mathematik Integralgleichung genannt, wenn darin die unbekannte Funktion in einem Integral vorkommt. Integralgleichungen können in Naturwissenschaft und Technik zur Beschreibung verschiedener Phänomene verwendet werden. Ein bekanntes Beispiel für eine Integralgleichung mit einigen Anwendungen ist die Abelsche Integralgleichung, die auch historisch zu den ersten untersuchten Integralgleichungen zählt.
Das Teilgebiet der Mathematik, das sich mit Integralgleichungen und den unten erwähnten kompakten Operatoren beschäftigt, ist die Funktionalanalysis.
Inhaltsverzeichnis
Definition
Eine lineare Integralgleichung ist eine Gleichung für eine unbekannte Funktion u und hat für
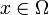 die Form
die Form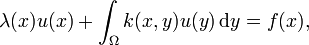
wobei λ, f, k gegebene Funktionen und
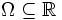 kompakt sind. Die Funktion k wird Kern genannt. Nichtlineare Gleichungen können noch komplizierter sein, z.B. kann u im Kern vorkommen: k(x,y,u(x)).
kompakt sind. Die Funktion k wird Kern genannt. Nichtlineare Gleichungen können noch komplizierter sein, z.B. kann u im Kern vorkommen: k(x,y,u(x)).Klassifizierung
Lineare Integralgleichungen kann man in
- Integralgleichungen 1. Art, wenn
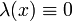 ,
, - Integralgleichungen 2. Art, wenn
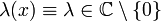 , und
, und - Integralgleichungen 3. Art, für alle anderen λ,
einteilen.
Diese Einteilung erscheint willkürlich, ist aber aufgrund der unterschiedlichen analytischen Eigenschaften der jeweiligen Arten von Integralgleichungen notwendig. So sind beispielsweise Integralgleichungen 2. Art (unter schwachen Voraussetzungen an den Kern) für fast alle Werte von λ eindeutig lösbar, und die Lösung hängt stetig von f ab. Dies gilt für Integralgleichungen 1. Art (unter denselben Voraussetzungen an den Kern) im Allgemeinen nicht. Integralgleichungen 1. Art sind wie z.B. die Laplace-Transformation fast immer inkorrekt gestellte Probleme. Die Fourier-Transformation bildet eine der wenigen Ausnahmen.
Ist die in einer Integralgleichung vorkommende bekannte Funktion
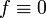 , so ist die Gleichung homogen, andernfalls inhomogen.
, so ist die Gleichung homogen, andernfalls inhomogen.Außerdem kann man Integralgleichungen nach ihren Integrationsgrenzen klassifizieren. Sind alle Grenzen konstant, so spricht man von Fredholm-Integralgleichungen, ist eine der Grenzen variabel, so nennt man die Gleichung eine Volterra-Integralgleichung.
Eine weitere Einteilung beruht auf Eigenschaften des Kerns. Hier gibt es schwach singuläre und stark singuläre Integralgleichungen.
Kompakte Operatoren
Mit
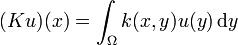 wird für einen hinreichend integrierbaren Kern k(x,y) ein linearer Operator K definiert. Wesentlich für die Theorie der (nicht stark singulären) Integralgleichungen ist die Theorie der kompakten Operatoren. Diese Theorie ähnelt in gewisser Weise der von linearen Gleichungen im Endlichdimensionalen. Kompakte Operatoren haben nämlich im Wesentlichen pure Eigenwertspektren. Genauer heißt das: Das Spektrum besteht (evtl. von der Null abgesehen) nur aus Eigenwerten und diese häufen sich in höchstens einem Punkt, der Null. Alle Eigenräume (evtl. von dem der Null abgesehen) sind endlichdimensional.
wird für einen hinreichend integrierbaren Kern k(x,y) ein linearer Operator K definiert. Wesentlich für die Theorie der (nicht stark singulären) Integralgleichungen ist die Theorie der kompakten Operatoren. Diese Theorie ähnelt in gewisser Weise der von linearen Gleichungen im Endlichdimensionalen. Kompakte Operatoren haben nämlich im Wesentlichen pure Eigenwertspektren. Genauer heißt das: Das Spektrum besteht (evtl. von der Null abgesehen) nur aus Eigenwerten und diese häufen sich in höchstens einem Punkt, der Null. Alle Eigenräume (evtl. von dem der Null abgesehen) sind endlichdimensional.Dualität von Integral- und Differentialgleichungen
Integraloperatoren treten oft (aber nicht ausschließlich) bei der Lösung von Differentialgleichungen auf, zum Beispiel bei Sturm-Liouville-Problemen, oder bei partiellen Differentialgleichungen in Form der Greenschen Funktion. Falls in der Gleichung zusätzlich noch eine Ableitung der Funktion vorkommt, spricht man von Integro-Differentialgleichungen. Ein Beispiel hierfür ist die aus der kinetischen Gastheorie stammende Boltzmann-Gleichung.
Literatur
- David Hilbert Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen, Leipzig, Berlin: B. G. Teubner, 1912.
- Adolf Kneser Die Integralgleichungen und ihre Anwendungen in der mathematischen Physik, Braunschweig: Friedr. Vieweg & Sohn 1922.
- Richard Courant und David Hilbert Methoden der mathematischen Physik Band 1, Berlin: Julius Springer, 1924. (Drittes Kapitel)
- Integralgleichungen 1. Art, wenn
Wikimedia Foundation.
