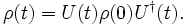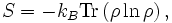- Dichteoperator
-
In der Physik beschreibt man mit einer Dichtematrix bzw. einem Dichteoperator (auch statistische Matrix bzw. statistischer Operator) einen Quantenzustand, über den man nicht die maximal mögliche Kenntnis besitzt. Die Dichtematrix enthält die maximale Information über Ergebnisse, die man durch Messungen (ausschließlich) an dem mit der Dichtematrix beschriebenen System erhalten kann.
Inhaltsverzeichnis
Definition
Betrachten wir ein quantenmechanisches System, welches auf einem Hilbertraum H modelliert ist. Ein beschränkter linearer Operator ρ auf H ist ein Dichteoperator, wenn gilt:
- er ist positiv semidefinit,
- er ist Spurklasse mit Spur gleich 1.
Eigenschaften
- Jeder Dichteoperator ist selbstadjungiert (oder hermitesch), da positive Operatoren immer selbstadjungiert sind.
- Die Menge aller Dichteoperatoren ist eine konvexe Menge, deren Rand die Menge der reinen (quantenmechanischen) Zustände ist. Die Menge ist, im Gegensatz zu klassischen Theorien, kein Simplex, d. h. ein Dichteoperator ist im Allgemeinen nicht eindeutig als Konvexkombination von reinen Zuständen darstellbar.
- Die Wahrscheinlichkeit, bei der Messung einer Observablen A an einem System, das durch den Dichteoperator ρ beschrieben wird, den Messwert a zu erhalten ist durch
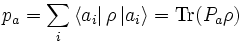
- gegeben, wobei
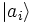 die orthonormierten Eigenvektoren zum Eigenwert a sind und Pa der Projektor auf den entsprechenden Eigenraum.
die orthonormierten Eigenvektoren zum Eigenwert a sind und Pa der Projektor auf den entsprechenden Eigenraum.
- Der Mittelwert der Messwerte bei der Messung einer Observablen A ist
Obwohl die Begriffe Dichtematrix und Dichteoperator oft synonym gebraucht werden, besteht ein mathematischer Unterschied. Genau wie in der linearen Algebra eine Matrix die Basisdarstellung eines linearen Operators ist, kann in der Quantenmechanik zwischen abstraktem Dichteoperator und einer konkreten Dichtematrix in einer bestimmten Darstellung unterschieden werden. Ist ρ ein Dichteoperator, so bezeichnet
z. B. die Dichtematrix in Ortsdarstellung. Die Dichtematrix in Ortsdarstellung ist allerdings keine echte Matrix, da die Ortsdarstellung über ein Kontinuum von uneigentlichen Basisvektoren | x > definiert ist, sondern ein so genannter Integralkern. In endlichdimensionalen Hilberträumen (z. B. bei Spinsystemen) erhalten wir dagegen eine echte Matrix, wenn wir eine Orthonormalbasis
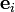 wählen:
wählen:Im Folgenden werden die beiden Begriffe allerdings wieder synonym verwendet, da sich die konkrete Bedeutung zumeist aus dem Zusammenhang erschließt.
Konstruktion von Dichtematrizen
Reine Zustände
Ist |Ψ> ein reiner Zustand, so ist der Projektionsoperator
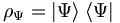 .
.
der zugehörige Dichteoperator. Hierbei gilt:
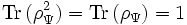 . Umgekehrt folgt aus dieser Bedingung bereits, dass ρΨ einen reinen Zustand beschreibt. Für gemischte Zustände gilt stets
. Umgekehrt folgt aus dieser Bedingung bereits, dass ρΨ einen reinen Zustand beschreibt. Für gemischte Zustände gilt stets 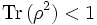 .
.Maximale Unkenntnis
Ein N-Level-System, über das man keinerlei Kenntnis hat, kann über die Dichtematrix
beschrieben werden, wobei
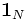 die N-dimensionale Einheitsmatrix bezeichnet.
die N-dimensionale Einheitsmatrix bezeichnet.Ensembles
Der quantenmechanische Zustandsbegriff ist von seiner Natur her statistisch zu sehen. Selbst bei bestmöglicher Präparation eines quantenmechanischen Systems (d.h. maximale Kenntnis im obigen Sinne) kann das System zwar durch einen reinen Zustand beschrieben werden, doch lassen sich selbst dann im Allgemeinen keine Aussagen über den Ausgang eines Einzelexperiments treffen. Vielmehr sind alle Aussagen über den Ausgang eines Versuchs statistisch, d. h. es werden Mittelwerte, Standard-Abweichungen und andere Momente von Wahrscheinlichkeitsverteilungen vorhergesagt. Der Ursprung dieses Charakters der Quantenmechanik kann in der Heisenberg'schen Unschärferelation gesehen werden.
Die Quantenmechanik trifft daher keine Aussagen über einzelne Messungen an einem System, sondern vielmehr über die möglichst oft wiederholte Messung unter den gleichen Präparationsbedingungen. Daher ist es auch zweifelhaft, ob der Begriff Zustand als die Beschreibung der Eigenschaften eines konkreten einzelnen Quantensystems zulässig ist. Die moderne Interpretation der Quantenmechanik versteht unter diesem Begriff die Gesamtheit von sehr vielen (im Idealfall beliebig vielen) unter gleichen Bedingungen unabhängig von einander präparierten Systemen gleicher Art. Diese Gesamtheit wird als Ensemble bezeichnet.
Der Begriff des Ensembles legt es nun nahe, den Zustandsbegriff in der gleichen Weise wie in der statistischen Mechanik zu erweitern. Wir sehen nämlich, dass zwar jeder reine Zustand ein Ensemble definiert, allerdings sind nicht alle Ensembles quantenmechanischer Zustände durch reine Zustände zu charakterisieren. Der Grund dafür liegt in der Tatsache, dass niemand den Präparator in dem obigen Schema dazu zwingt, möglichst exakt zu präparieren. Der einfachste Fall ist z. B., dass bei der Präparation zufällig mit gewissen Wahrscheinlichkeiten zwischen verschiedenen "reinen" Präparationen gewechselt wird. Eine solche Präparation nennt man ein Gemisch. Liegt z. B. ein Gemisch verschiedener Zustände vor, bei der mit Wahrscheinlichkeit pi der reine Zustand
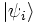 präpariert wurde, so wird dieses Ensemble durch die Dichtematrix
präpariert wurde, so wird dieses Ensemble durch die Dichtematrixbeschrieben. Man beachte, dass die einzelnen Terme dieser Summe keine Information über die globale Phase der Zustände
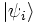 enthalten, es sich also bei einem gemischten Zustand nicht um eine kohärente Superposition von reinen Zuständen handelt.
enthalten, es sich also bei einem gemischten Zustand nicht um eine kohärente Superposition von reinen Zuständen handelt.Allgemein kann man zeigen, dass jedes Ensemble, insbesondere solche, die durch schlechte Präparation entstehen, durch gemischte Zustände definiert werden können. Allerdings lassen sich solche Zustände, im Gegensatz zur klassischen statistischen Mechanik, nicht eindeutig in reine Zustände zerlegen. Verschiedene Gemische können den gleichen Zustand definieren. Dies ist ein weiterer Grund dafür, dass es unzulässig ist, gemischte Zustände als Ensemble von reinen Zuständen, die alle ein Einzelsystem beschreiben, aufzufassen.
Zeitentwicklung
Aus der Schrödingergleichung, die die Zeitentwicklung (Dynamik) reiner Quantenzustände beschreibt, kann man unmittelbar die Zeitentwicklung gemischter Zustände ableiten. Dazu benutzt man eine beliebige Zerlegung der Dichtematrix in reine Zustände, deren Dynamik der Schrödinger-Gleichung genügt, und berechnet daraus die Dynamik des gemischten Zustandes zu
wobei H der Hamilton-Operator des Systems ist. Diese Gleichung ist als von-Neumann'sche Bewegungsgleichung bekannt (
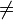 Heisenberg'sche Bewegungsgleichung).
Heisenberg'sche Bewegungsgleichung).Man kann für zeitunabhängige Hamilton-Operatoren diese Differentialgleichung leicht integrieren und erhält mit dem unitären Zeitentwicklungs-Operator
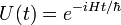 die Gleichung
die GleichungBemerkenswert ist hierbei, dass für diesen Operator die übliche Heisenberg'sche Bewegungsgleichung nicht gilt, da ρ keine Observable ist. Auch die Transformation mit dem Zeitentwicklungsoperator ist nicht gemäß der üblichen Zeitentwicklungsgleichung für Operatoren.
Entropie
Eine mögliche Entropie-Definition einer Dichtematrix ρ ist die Von-Neumann-Entropie. Diese lautet:
wobei kB die Boltzmannkonstante ist, und die Spur über dem Raum H genommen ist, in dem ρ operiert.
Die Entropie jedes reinen Zustands ist Null, da die Eigenwerte der Dichtematrix Null und Eins sind. Dies stimmt mit der heuristischen Argumentation, dass keine Unsicherheit über die Präparation des Zustandes herrscht, überein.
Man kann zeigen, dass unitäre Operatoren angewendet auf einen Zustand (wie der aus der Schrödinger-Gleichung gewonnene Zeitentwicklungs-Operator) die Entropie des Systems nicht ändern. Das verbindet die Reversibilität eines Prozesses mit seiner Entropieänderung - ein fundamentales Ergebnis, das die Quantenmechanik mit der Informationstheorie und der Thermodynamik verbindet.
Weblinks
Artikel von Lieven Smits aus Antwerpen über De dichtheidsmatrix in de statistische mechanica
Wikimedia Foundation.

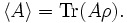
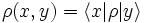
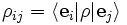
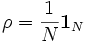
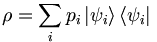
![\dot{\rho}=\frac{i}{\hbar}[\rho,H],](/pictures/dewiki/99/cc3936a54b86e902be5f3006a0a7371c.png)