Isentropenexponent

Spezialfälle der polytropen Zustandsänderung; n = 0: isobar, n = 1: isotherm, n = κ: isentrop, n = unendlich: isochor

Der Isentropenexponent (Formelzeichen: κ) ist der Exponent in der Gleichung

$\ pV^{\kappa}= \mathrm{const.}$

für die isentrope Zustandsänderung eines idealen Gases.

Da eine Zustandsänderung isentrop ist, wenn sie adiabat und reversibel verläuft, wie das z. B. bei großräumigen Luftströmungen angenähert der Fall ist, nennt man den Exponenten in der Meteorologie auch oft Adiabatenexponent, Adiabatenkoeffizient oder Adiabatenindex. In der Technik ist in der Regel eine adiabate Zustandsänderung (z. B. in einer Dampfturbine) nicht isentrop, da Reibungs-, Drossel- und Stoßvorgänge Entropie produzieren (vergl. „Adiabate Maschine“ und „Zweiter Hauptsatz der Thermodynamik“). Diese Zustandsänderungen lassen sich näherungsweise durch eine Polytrope mit einem variablen Polytropenexponenten n beschreiben.

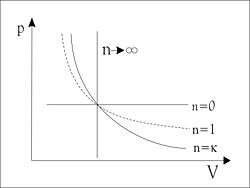
Die Isentrope ist der Spezialfall einer Polytrope mit n = κ (vergl. Bild).

Isentropenexponenten für Gase bei Normaldruck
Temp	Gas	κ		Temp	Gas	κ		Temp	Gas	κ
–181 °C	H2	1,60		0 °C	Trockene Luft	1,40		20 °C	N2O	1,31
–76 °C		1,45		400 °C		1,39		–181 °C	N2	1,47
20 °C		1,41		1000 °C		1,32		15 °C		1,40
100 °C		1,40		2000 °C		1,30		1000 °C		1,32
400 °C		1,39		0 °C	CO2	1,31		2000		1,30
1000 °C		1,38		20 °C		1,30		20 °C	Cl2	1,34
20 °C bis 1500 °C	He	1,67		100 °C		1,28		–115 °C	CH4	1,41
				400 °C		1,24		–74 °C		1,35
20 °C	H2O	1,33		1000 °C		1,18		20 °C		1,32
200 °C		1,31		2000 °C		1,18?		15 °C	NH3	1,31
500 °C		1,28		20 °C	CO	1,40		19 °C	Ne	1,64
1000 °C		1,23		–181 °C	O2	1,45		19 °C	Xe	1,66
–180 °C	Ar	1,76		–76 °C		1,42		19 °C	Kr	1,68
20 °C		1,67		20 °C		1,40		15 °C	SO2	1,29
				400 °C		1,39		360 °C	Hg	1,67
				1000 °C		1,31		15 °C	C2H6	1,22
				20 °C	NO	1,40		16 °C	C3H8	1,13

Der Isentropenexponent ist definiert als das Verhältnis der spezifischen Wärmekapazitäten bei konstantem Druck (c_p) und konstantem Volumen (c_V). Der Wert hängt von der Zahl Z der Freiheitsgrade der Gasteilchen ab

$\kappa = \frac{c_p}{c_V} = \frac{Z + 2}{Z}$     bzw.     $Z = \frac{2}{\kappa - 1}$.

Z = Translationsfreiheitsgrade + Rotationsfreiheitsgrade + 2 $\cdot$ Schwingungsfreiheitsgrade

Die Zahl der Freiheitsgrade ist von der Atomzahl und räumlichen Anordnung des Gasmoleküls abhängig. Darüber hinaus weist κ auch eine Temperaturabhängigkeit auf, da Rotationen und Schwingungen nur bei höheren Temperaturen thermisch angeregt werden können. Mit abnehmender Temperatur "frieren" immer mehr Freiheitsgrade ein, insbesondere Schwingungsfreiheitsgrade.

Der Isentropenexponent von (trockener) Luft beträgt unter Normalbedingungen κ = 1,402 und liegt damit nahe bei 1,4, was der theoretische Wert für 3 Translations- und 2 Rotationsfreiheitsgrade (bei zweiatomigen Molekülen ist in diesem Sinne keine Rotation um die Verbindungsachse möglich, bei größeren Molekülen gibt es 3 Rotationsfreiheitsgrade) wäre; Schwingungszustände werden also kaum angeregt. Bei viel höheren Temperaturen kommt es neben den Molekülschwingungen durch Dissoziations- und Ionisationsvorgänge zu noch mehr Freiheitsgraden. Bei feuchter Luft kann es bei Expansion z. B. infolge der Abkühlung zum Wasserausfall kommen: durch die freiwerdende Kondensationswärme wird der Exponent niedriger.

Bestimmen lässt sich der Isentropenexponent mit Hilfe des Rüchardt-Experiments.

molare Wärmekapazität bei isochorer (C_V) bzw. bei isobarer (C_p) Zustandsänderung, sowie der Isentropenexponent κ

	CV	Cp	$\kappa=\frac{C_p}{C_v}$
1-atomige Gase	$\frac{3}{2} \cdot R$	$\frac{5}{2} \cdot R$	$\frac{5}{3}=1{,}\overline{6}$
2-atomige Gase	$\frac{5}{2} \cdot R$	$\frac{7}{2} \cdot R$	$\frac{7}{5}=1{,}4$
3-atomige Gase	$\frac{6}{2} \cdot R$	$\frac{8}{2} \cdot R$	$\frac{4}{3}=1{,}\overline{3}$

Literatur

• Böge Alfred, Handbuch Maschinenbau 2011 Vieweg+Teubner ISBN 3-8348-1025-8 ISBN 978-3-8348-1025-0 | KNV-Titelnr.: 28739068