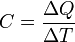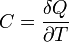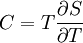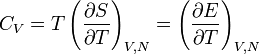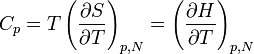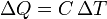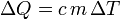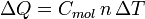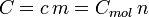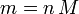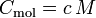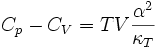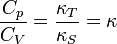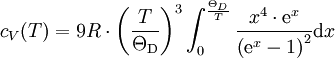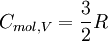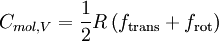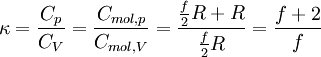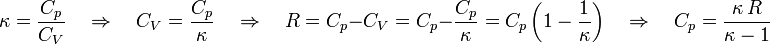- Molare Wärmekapazität
-
Die Wärmekapazität ist eine Materialeigenschaft und gibt an wie viel Wärme ΔQ ein Körper pro Temperaturänderung ΔT speichern kann.
Dabei wird unterschieden zwischen
- der Wärmekapazität C eines beliebigen Körpers mit der Einheit
![[C] = \mathrm{\tfrac{J}{K}}](/pictures/dewiki/102/f8834264516f7552b9e3f763094209ab.png) ,
, - der spezifischen Wärmekapazität c, die auf die Masse bezogen wird
![[c] = \mathrm{\tfrac{J}{kg \cdot K}}](/pictures/dewiki/100/d7de959b3493232f1c903c24c854126a.png) ,
, - der molaren Wärmekapazität Cmol (auch Molwärme), die auf die Stoffmenge bezogen wird
![[C_\mathrm{mol}] =\mathrm{\tfrac{J}{mol \cdot K}}](/pictures/dewiki/55/7289453bc5ddef981a5edcad9b700f50.png) und
und - der Wärmespeicherzahl s, die auf das Volumen bezogenen wird
![[s] = \mathrm{\tfrac{J}{m^{3} \cdot K}}](/pictures/dewiki/57/9296ac8d280f5689058980ef8fd1fb26.png) .
.
Inhaltsverzeichnis
Definition der Wärmekapazität
Genauer ist die Wärmekapazität ein Begriff aus der Thermodynamik und bezeichnet das Vermögen eines Körpers, Energie in Form von thermischer Energie statistisch verteilt auf die Freiheitsgrade zu speichern. Die Wärmekapazität gilt nicht über Phasengrenzen hinweg (siehe Schmelzwärme und Verdampfungswärme) und ist innerhalb eines Aggregatzustandes leicht von der Temperatur abhängig, was eine differentielle Betrachtung sinnvoll macht.
Man beachte dass die Wärme Q keine Zustandsgröße ist und somit auch kein totales Differential besitzt. Die zugeführte Wärme δQ hängt mit der Temperatur T und Entropie S über δQ = TdS zusammen, so dass für die Wärmekapazität gilt:
Dabei ist es vonnöten, dass der Prozess der Erwärmung quasi-statisch (d.h. sehr langsam) erfolgt, so dass während des Prozesses irreversible Erscheinungen keine wesentliche Rolle spielen. Präziser sollte man deshalb von der Gleichgewichtswärmekapazität sprechen.
Im Allgemeinen spielen die äußeren Bedingungen, unter denen der Körper erwärmt wird, wie konstanter Druck p oder konstantes Volumen V, sowie konstante Teilchenzahl N eine Rolle. Bei konstantem Druck wird beispielsweise gleichzeitig Arbeit in Form der thermischen Ausdehnung des Körpers geleistet, was auf Grund der Energieerhaltung zu einer größeren Wärmeaufnahme pro Temperatureinheit führt. Man unterscheidet deshalb die Wärmekapazität für ein konstantes Volumen, die isochore Wärmekapazität CV, und für einen konstanten Druck, die isobare Wärmekapazität Cp.
Dabei ist E(S,V,N) die Innere Energie mit dE = TdS − pdV + μdN und H(S,p,N) die Enthalpie mit dH = TdS + Vdp + μdN.
Ist der Körper physikalisch homogen, so ist es sinnvoll, die Wärmekapazität pro Masseneinheit (oder Stoffeinheit) anzugeben, welche dann als spezifische Wärmekapazität c (beim Bezug auf 1 kg eines Stoffs) oder Molwärme bzw. molare Wärmekapazität cn (beim Bezug auf 1 mol eines Stoffs) bezeichnet wird.
Die physikalische Einheit der Wärmekapazität ergibt sich aus ihrer Definition als [J/K], die der spezifischen Wärmekapazität je nach bezogener Stoffeinheit als [J/(kg·K)] oder [J/(mol·K)].
Auch die Temperatur des Stoffes hat einen Einfluss auf die (spezifische) Wärmekapazität. Dies sieht man an folgendem Beispiel:
- Wasser bei 20 °C:
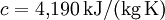
- Wasser bei 15 °C:
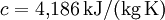
Für feste Stoffe kann man in kleinen Temperaturbereichen eine mittlere spezifische Wärmekapazität verwenden.
Bestimmung der Wärmekapazität
Die Wärmekapazität eines Stoffes wird mit Hilfe eines Kalorimeters bestimmt, zum Beispiel mit der Dynamischen Differenzkalorimetrie (DSC). Wichtig für die Messung ist dabei, dass die zu untersuchende Probe in dem zu untersuchenden Temperaturbereich keine mit einer Wärmetönung einhergehenden Reaktion aufweist. Üblicherweise erfolgt zur exakten Berechnung eine Vergleichsmessung mit einem Saphir.
Allgemeine Beziehungen
Die Gleichung für die Wärmekapazität ist:
Die Gleichung, die Wärme, Masse, Temperaturänderung und spezifische Wärmekapazität in Zusammenhang zu bringen, ist:
Und die Gleichung für die molare Wärmekapazität ist:
dabei ist ΔQ die Wärme, die der Materie zugeführt oder entzogen wird,
m ist die Masse der Substanz,
n ist die Stoffmenge,
c ist die spezifische Wärmekapazität und
ΔT ist die Temperaturänderung.Die verschiedenen Wärmekapazitäten hängen zusammen über:
Über die Beziehung zwischen Masse und Stoffmenge
mit der molaren Masse M folgt der Zusammenhang zwischen molarer (Cmol) und spezifischer (c) Wärmekapazität:
Am Beispiel Kupfer ergibt sich:
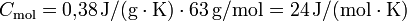
Verknüpfung mit anderen thermodynamischen Größen
Wie weiter unten beschrieben ist stets Cp > CV. Die beiden Größen sind über folgende Beziehungen miteinander verknüpft:
Hierbei ist
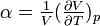 der thermische Ausdehnungskoeffizient,
der thermische Ausdehnungskoeffizient,
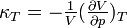 die isotherme Kompressibilität,
die isotherme Kompressibilität,
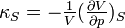 die isentrope bzw. adiabatische Kompressibilität,
die isentrope bzw. adiabatische Kompressibilität,
κ der Isentropenexponent und
T die absolute Temperatur (in Kelvin).Wärmekapazität von Festkörpern
Debye-Temperatur ausgewählter Materialien Material Debye-Temperatur Aluminium 426 K Magnesium 406 K Eisen 464 K Kupfer 345 K Zinn 195 K Blei 96 K Bei Festkörpern ist für schwere Elemente und hohe Temperaturen in guter Näherung das Dulong-Petit-Gesetz erfüllt, das eine konstante molare Wärmekapazität von
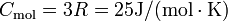 für den Festkörper vorhersagt.
für den Festkörper vorhersagt.Bei niedrigen Temperaturen versagt dieses Modell. In diesem Bereich sagt das Debye-Modell eine T3-Abhängigkeit der Wärmekapazität vorher. Nach dem Debye-Modell wird die molare Wärmekapazität in Abhängigkeit von der Temperatur durch nur eine Stoffgröße, die sogenannte Debye-Temperatur ΘD, bestimmt:
Der Vorläufer des Debye-Modells ist das Einstein-Modell, welches insbesondere bei tiefen Temperaturen für praktische Anwendungen zu ungenau ist.
Wärmekapazität idealer Gase
Verknüpfung Cp und CV
Insbesondere bei Gasen hängt die Wärmekapazität von den äußeren Zwangsbedingungen ab. Man unterscheidet die Wärmekapazität bei konstantem Druck Cp und bei konstantem Volumen CV. Bei isochoren Zustandsänderungen wird die zugeführte Wärmemenge komplett zur Erhöhung der Temperatur des Gases (also zur Erhöhung der kinetischen Energie der Gasteilchen) aufgewendet. Bei isobaren Prozessen hingegen muss Volumenarbeit verrichtet werden, da sich das Gas beim Erwärmen ausdehnen muss, wenn der Druck konstant bleiben soll. Das heißt, bei konstantem Druck wird ein Teil der zugeführten Wärmeenergie in Form von Volumenarbeit „verbraucht“. Deshalb muss bei isobaren Zustandsänderungen mehr Wärmeenergie zugeführt werden um ein Gas um ein Grad zu erwärmen als bei isochoren Zustandsänderungen.
Für ideale Gase gilt:
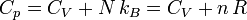 .
.
Hierbei ist N die Teilchenzahl, kB die Boltzmann-Konstante, n die Stoffmenge und
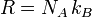 die universelle Gaskonstante. Für 1 mol ergibt dies:
die universelle Gaskonstante. Für 1 mol ergibt dies: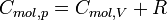 .
.
Beispiel - Wasserstoff (H2) bei 20 °C und 1,013 bar, experimentell gemessene Werte:
- bei gleichbleibendem Druck:
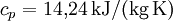
- bei gleichbleibendem Volumen:
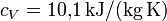
Die Differenz der experimentell gemessenen Größen
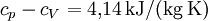 statt
statt 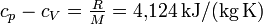 aus der theoretischen Überlegung erklärt sich daraus, dass Wasserstoff kein hundertprozentig ideales Gas ist.
aus der theoretischen Überlegung erklärt sich daraus, dass Wasserstoff kein hundertprozentig ideales Gas ist.Ab initio Berechnung von CV
Um die Wärmekapazität idealer Gase zu überschlagen, gibt es die Möglichkeit, sie über die Freiheitsgrade zu berechnen. Nach dem Gleichverteilungssatz ist die Gesamtenergie eines Gases aus N identischen Teilchen (Atome, Moleküle) gleich
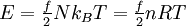 . Aus
. Aus 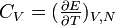 folgt:
folgt: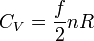 bzw.
bzw. 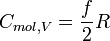
wobei
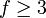 die Anzahl der energetischen Freiheitsgrade eines Moleküls angibt. Jedes Atom hat drei Freiheitsgrade, nämlich die Translationen in den drei Raumdimensionen. Die Freiheitsgrade eines Moleküls umfassen:
die Anzahl der energetischen Freiheitsgrade eines Moleküls angibt. Jedes Atom hat drei Freiheitsgrade, nämlich die Translationen in den drei Raumdimensionen. Die Freiheitsgrade eines Moleküls umfassen:- ftrans = 3, drei Freiheitsgrade für die Translation,
![f_\mathrm{rot}\in [0;3]](/pictures/dewiki/51/34738519c34f849b056bbe92a79d41c1.png) , Null bis drei Freiheitsgrade für die Rotationsenergie und
, Null bis drei Freiheitsgrade für die Rotationsenergie und- fvib = 3A − ftrans − frot Freiheitsgrade für die innere Schwingungsenergie. A ist dabei die Gesamtzahl der Atome des Moleküls.
Ein zweiatomiges Molekül A = 2 hat ftrans = 3, frot = 2 und
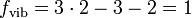 . Ein dreiatomiges gewinkeltes Molekül A = 3 hat ftrans = 3, frot = 3 und fvib = 3. Einzelne Atome A = 1 besitzen nur drei translatorische Freiheitsgrade ftrans = 3.
. Ein dreiatomiges gewinkeltes Molekül A = 3 hat ftrans = 3, frot = 3 und fvib = 3. Einzelne Atome A = 1 besitzen nur drei translatorische Freiheitsgrade ftrans = 3.Für Gase, deren Bestandteile einzelne Atome sind, gilt:
Für Gase, deren Bestandteile A-atomige Moleküle sind, gilt:
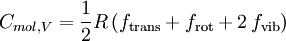 mit
mit 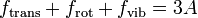
Jeder Translations- bzw. Rotationsfreiheitsgrad trägt also mit
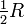 zur molaren Wärmekapazität bei, jeder Vibrationsfreiheitsgrad mit R. Dabei ist zu beachten, dass bei Raumtemperatur üblicherweise alle möglichen Rotationen angeregt sind (IR-Spektrum), Vibrationen (also Schwingungen) dagegen häufig nur zu einem geringen Anteil (UV-Spektrum). Im Grenzfall der vollständigen Vernachlässigung der Schwingungen erhält man:
zur molaren Wärmekapazität bei, jeder Vibrationsfreiheitsgrad mit R. Dabei ist zu beachten, dass bei Raumtemperatur üblicherweise alle möglichen Rotationen angeregt sind (IR-Spektrum), Vibrationen (also Schwingungen) dagegen häufig nur zu einem geringen Anteil (UV-Spektrum). Im Grenzfall der vollständigen Vernachlässigung der Schwingungen erhält man:molare Wärmekapazität bei isochorer (CV) bzw. bei isobarer (Cp) Zustandsänderung, sowie der Isentropenexponent κ CV Cp κ 1-atomige Gase 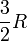
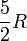

2-atomige Gase 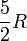
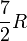

Beispiel - Wasserstoff (H2) bei Raumtemperatur: ftrans = 3, frot = 2, 2fvib = 2. Es wird die spezifische Gaskonstante
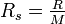 verwendet:
verwendet:- ohne Vibrationen:
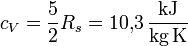 und
und 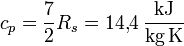
- mit Vibrationen:
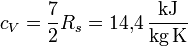 und
und 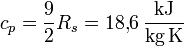
Durch Vergleich dieser Zahlen mit den gemessenen Werten
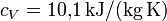 und
und 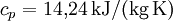 sieht man also, dass Vibrationen hier nicht angeregt sind.
sieht man also, dass Vibrationen hier nicht angeregt sind.Isentropenexponent
Der Isentropenexponent κ des idealen Gases ist:
Sollte der Isentropenexponent κ des idealen Gases bekannt sein, so lassen sich die Wärmekapazitäten aus der Kombination von Cmol,p − Cmol,V = R und den folgenden Formeln berechnen:
Negative Kapazität (Sterne)
Die meisten physikalischen Systeme zeigen eine positive Wärmekapazität. Auch wenn das Gegenteil zunächst absurd erscheint, können Systeme auch eine negative Wärmekapazität aufweisen. Dazu zählen gravitierende Objekte wie zum Beispiel kollabierende Sterne, die sich beim Zusammenziehen (innere Energie verringert sich) erhitzen, oder sehr kleine Systeme (englisch Cluster) aus einigen hundert Atomen nahe an einer Phasenumwandlung. Diese merkwürdige Eigenschaft steht im Zusammenhang mit der thermodynamischen Stabilität. Nur Systeme mit einer positiven Wärmekapazität können im thermodynamischen Sinne als stabil und diese damit auch als extensive Größe betrachtet werden.
Literatur
- G. R. Stewart: Measurement of low-temperature specific heat. In: Rev. Sci. Instrum. Nr. 54, 1983, S. 1–11 (doi:10.1063/1.1137207)
- Michael Tausch: Chemie SII, Stoff - Formel - Umwelt. C.C. Buchners Verlag, Bamberg 1993, ISBN 978-3766164537
- Gustav Kortüm: Einführung in die chemische Thermodynamik. Verlag Chemie, Basel 1981, ISBN 3-527-25881-7 (bzw. Vandenhoeck & Ruprecht, Göttingen 1981, ISBN 3-525-42310-1)
- Walter J. Moore, Dieter O. Hummel: Physikalische Chemie. Verlag de Gruyter, Berlin/New York 1986, ISBN 3-11-010979-4
- David R. Lide: Handbook of Chemistry and Physics. 59. Ausgabe. CRC Press, Boca Raton 1978, ISBN 9780849304866, Seite D-210, D-211.
- Callen: Thermodynamics and an Introduction to Thermostatistics. Wiley & Sons. ISBN 978-0471862567
Weblinks
Verzeichnis von Datenbanken und Nachschlagewerken mit Wärmekapazitäten:
Wikimedia Foundation.