Kepler-Gleichung

Punkte: z: Periapsis; p: Objekt; c: Mittelpunkt; s: Brennpunkt. Winkel: E: Exzentrische-, T: Wahre-, M: Mittlere Anomalie.

Die Kepler-Gleichung ergibt sich aus den keplerschen Gesetzen durch Einführung der exzentrischen Anomalie E und der mittleren Anomalie M.

Mit ihrer Hilfe lässt sich das Kepler-Problem lösen, also die wahre Anomalie T, das ist der momentane Winkelabstand eines Himmelsobjekts von der Periapsis z auf seiner Keplerbahn, in Abhängigkeit von der Zeit berechnen.

Die moderne Formulierung unterscheidet sich etwas von der, die Johannes Kepler in seiner Astronomia Nova von 1609 publizierte.

Mittlere Anomalie

Die elliptische Bahnkurve (Orbit) wird um einen Umkreis als Hilfskreis erweitert.

Ein Punkt y auf dem Hilfskreis kann als fiktiver Himmelskörper angesehen werden, der zum Zeitpunkt t₀ ebenso wie das wahre Objekt in der Periapsis steht, dieselbe Umlaufzeit hat, aber mit konstanter Winkelgeschwindigkeit auf einer Kreisbahn umläuft, die den Radius der Ellipsen-Halbachse a hat.

Die mittlere Anomalie M wird als der Winkel zum mittleren Objekt im Hilfskreis-Mittelpunkt c im Bezug zur Periapsis z definiert (alle Winkel in Bogenmaß):

$M= 2 \pi \frac {t-t_0} {U}$

Dabei ist U die Bahnperiode und t₀ der Zeitpunkt, zu dem das Himmelsobjekt sich in der Periapsis befindet (die Periapsiszeit). Das Objekt hat zu diesem Zeitpunkt t₀ den geringsten Abstand zu seinem Schwerezentrum. 2π / U ist die mittlere Bewegung n.

Nach dem zweiten keplerschen Gesetz überstreicht der Fahrstrahl vom Objekt zum Schwerezentrum in gleichen Zeiten den gleichen Anteil der Gesamtfläche der Bahn.

Da beide Objekte zur selben Zeit durch die Periapsis gehen, ist die überstrichene Gesamtfläche πab für P und πa² für y.

Die Definition des mittleren Objekts y besagt also, dass sein Fahrstrahl $\overline {cy}$ im Verhältnis dieselbe Fläche überstreicht wie der Fahrstrahl $\overline {sP}$des Körpers P:

$\frac{\operatorname{area}\,cyz}{\operatorname{area}\,sPz} = \frac{\pi a^2}{\pi a b} = a/b$

mit der Funktion $\operatorname{area}\,ABC$, die die Fläche des Kreis- bzw. Ellipsensektors ABC berechnet

Exzentrische Anomalie

Ein Hilfspunkt x ist die Projektion von P auf den Hilfskreis.

Die exzentrische Anomalie E ist der Winkel im Mittelpunkt c von der Periapsis z zu x.

Der Normalabstand von x zur Linie $\overline {cz}$ ist also um den Faktor a / b größer als der Abstand des Objekts P, und daher ist auch die von der Verbindungslinie vom Schwerezentrum s zu x überstrichene Fläche um den Faktor a / b größer als die vom Fahrstrahl $\overline {sP}$ überstrichene Fläche.

$\operatorname{area}\,sxz = \frac ab\operatorname{area}\,sPz$

Der Hilfspunkt ist also so konstruiert, dass er immer dieselbe Fläche wie das mittlere Objekt überstreicht:

$\operatorname{area}\,sxz = \operatorname{area}\,cyz$

Keplergleichung

Wenn der Fahrstrahl von y nun in einer Periode U den Winkel 2π zurücklegt und die Fläche πa² überstreicht, hat er zum Zeitpunkt t beim Winkel M eine um den Faktor M / 2π kleinere Fläche überstrichen, und da auch x als Projektion zum Zeitpunkt t₀ durch z läuft:

$\operatorname{area}\,cyz = \frac{a^2}{2} M$ und $\operatorname{area}\,cxz = \frac{a^2}{2} E$

Das Dreieck cxs besteht aus der Grundlinie $a \cdot e$ (mit der numerischen Exzentrizität e der Ellipse, die den Abstand zwischen Mittelpunkt und Brennpunkt im Verhältnis zur großen Halbachse gibt, und in diesem steht nach dem ersten Keplergesetz das Schwerezentrum) und der Höhe $a \cdot \sin E$:

$\operatorname{area}\,cxs = \frac{a^2}{2} e \sin E$

Durch Zerlegung der Flächen und der Definition von y und x folgt also:

$\mbox{area}\,cxz=\operatorname{area}\,cxs + \operatorname{area}\,sxz$$= \operatorname{area}\,cxs + \operatorname{area}\,cyz$

also

$\frac{a^2}2E=\frac{a^2}{2} e \sin E+\frac{a^2}2M$

Daraus leitet sich schließlich die Kepler-Gleichung ab:

$E - e \cdot \sin E = M$

Für diese Ableitung werden nur die keplerschen Gesetze benötigt. Diese Gesetze können, wie Isaac Newton später zeigen konnte, aus dem Gravitationsgesetz abgeleitet werden, das Kepler jedoch nicht bekannt war.

Kepler selbst bezeichnete M als „mittlere Bewegung“ und E − e·sinE als „mittlere Anomalie“.

Berechnung der exzentrischen Anomalie

Die Größe E(t) kann als Nullstelle der Funktion der Keplergleichung betrachtet werden:

$f(E) = E - e \cdot \sin E - 2 \pi \frac {t-t_0} {U}$

Die Nullstelle kann etwa mit dem Newton-Verfahren numerisch berechnet werden.

Eine stabileres, aber langsamer konvergierendes Verfahren beruht auf dem banachschen Fixpunktsatz:

$E_n = M + e \cdot \sin E_{n-1}; ~ E_0 = M$ ^[1]

Für kleine Exzentrizität e kann E auch folgendermaßen approximiert werden:

$E = M + e \cdot \sin M + \frac{1}{2} e^2 \cdot \sin 2M$ ^[2]

Der Fehler ist hierbei von der Größenordnung $\mathcal{O}(e^3)$. Bei der Erde und ihrer Exzentrizität e = 0,0167 liegt der Fehler für begrenzte Zeiträume also hinter der 5. Kommastelle.

Wahre Anomalie

Die gesuchte wahre Anomalie T zu einem Zeitpunkt t lässt sich aus E berechnen:

$\tan \frac{T}{2} = \sqrt{\frac{1+e}{1-e}} \cdot \tan \frac{E}{2}$^[3]

oder

$T = \arccos \left( \frac {\cos E - e}{1-e \cos E} \right)\,,\, 0 \le E \le \pi$

$T = 2 \pi - \arccos \left( \frac {\cos E - e}{1-e \cos E} \right)\,,\, \pi \le E \le 2\pi$^[3]

Zwischen den Anomalien T, E und M bestehen noch zahlreiche weitere Zusammenhänge^[4], die in der langen Geschichte der Himmelsmechanik entwickelt wurden, und insbesondere lässt sich die wahre Anomalie – ohne Umweg über die Keplergleichung – direkt aus einer speziellen Differenzialgleichung in M errechnen^[5], was für numerische Näherungsverfahren von Interesse ist.

Ideale Keplerbahn

Keplerbahnen

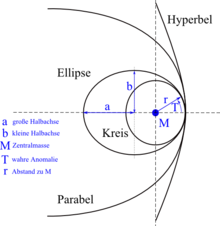
Mit der idealen, ungestörten Keplerbahn kann eine Bestimmung des Radius und der Geschwindigkeit in Bezug zur wahren Anomalie erfolgen. Die Keplerbahnen können in vier Orbitklassen unterteilt werden (siehe Abb.), wobei man in der Regel bei einer idealen Keplerbahn meist von einem elliptischen Orbit spricht.

Kreisorbit	e = 0
Elliptischer Orbit	e < 1
Parabolischer Orbit	e = 1
Hyperbolischer Orbit	e > 1

Bei realen astronomischen Objekten ist die Bewegung aber Bahnstörungen unterworfen, die diese Werte verfälschen. Aus diesem Grund ist die ideale Keplerbahn eine eher mathematisch-theoretische Flugbahn, die jedoch in vielen Fällen, unter Berücksichtigung von möglichen Bahnstörungen und der benötigten Genauigkeit der Flugbahn, zur Berechnung des Bewegungsablaufs verwendet werden kann (z. B. bei Überschlagsrechnungen). Dies erschwert die Bestimmung von Ort und Geschwindigkeit eines astronomischen Objekts, das die Grundaufgabe der Bahnbestimmung ist. Bei manchen Objektklassen werden diese elementaren Bahndaten direkt als Bahnelement angegeben.

Diese Daten bilden dann die Grundlage für alle weiteren Berechnungen der Himmelsmechanik, der astronomischen Phänomenologie, beobachtenden Astronomie, Ephemeridenrechnung wie auch der Raumfahrt.

Bahnradius

Aus der wahren Anomalie kann dann die Entfernung des Körpers für eine Zeit t bestimmt werden:

$r = r(T(t)) = r(t) = a \cdot \frac{(1-e^2)}{1+e \cdot \cos T}$

r: Entfernung (Bahnradius)

a: große Halbachse der Ellipse

e: Numerische Exzentrizität

T: wahre Anomalie

Bahngeschwindigkeit

Die wahre Anomalie ist die Winkelgeschwindigkeit ω im Gravizentrum. Die Normalkomponente der Geschwindigkeit folgt also direkt aus

$v_\perp = T \cdot r$

Die Radialgeschwindigkeit ist die Änderung des Bahnradius mit der Zeit:

$v_r = \dot r$

Die Bahngeschwindigkeit oder Orbitalgeschwindigkeit folgt dann zu $v^2= v_\perp^2 + v_r^2$

$v = v(T(t), r(t)) = v(t) = \sqrt{ (T \cdot r)^2 + \dot r^2}$

v: Bahngeschwindigkeit

T: wahre Anomalie

r: Bahnradius

Einfacher lässt sich die Bahngeschwindigkeit über den Hodograph $\vec {\dot r}$ aus dem Flächensatz ableiten

$v^2 = \frac {C^2}{p} \left( \frac {2}{r} - \frac {1}{a} \right)$^[6]

C: Bahndrehimpuls als zentrale Kenngröße der Bewegung

$C = v_\mathrm{max}\cdot r_\mathrm{min} = v_\mathrm{min}\cdot r_{max}$

p: Parameter als kennzeichnendes Bahnelement

$p = 2 \cdot \frac{r_\mathrm{min}\cdot r_\mathrm{max}}{r_\mathrm{min} + r_\mathrm{max}} = \frac{b^2}{a}$

a: große Halbachse

b: kleine Halbachse

Daraus folgen die Minimal- und Maximalgeschwindigkeit im Apozentrum und Perizentrum einer Ellipsenbahn

$v_\mathrm{max}^2 = \frac {C^2}{p\cdot a}\cdot\frac{1 + e}{1 - e} \qquad v_\mathrm{min}^2 = \frac{C^2}{p\cdot a} \cdot\frac{1 - e}{1 + e}$^[6]

e: numerische Exzentrizität

Siehe auch

• Keplersche Gesetze

Literatur

• Andreas Guthmann: Einführung in die Himmelsmechanik und Ephemeridenrechnung. BI-Wiss.-Verl., Mannheim 1994, ISBN 3-411-17051-4

Einzelnachweise

1. ↑ §II.6.67 Numerische Verfahren. Guthmann, S. 128f
2. ↑ §II.6.66 Reihenentwicklung der exzentrischen Anomalie. Guthmann, S. 125ff
3. ↑ ^{a b} §II.5.57 Berechnung des Bahnortes. Guthmann, S. 112ff
4. ↑ Aufgaben zu §II.5. Guthmann, S. 122f
5. ↑ 10. Aufgabe zu §II.5. Guthmann, S. 123
6. ↑ ^{a b} §II.5.58 Der Hodograph. Guthmann, S. 114f