Jeans-Kriterium

Das Jeans-Kriterium (auch Jeanssches Kriterium, benannt nach James Jeans) ist eine Bedingung für die Stabilität, ob eine kosmische Gaswolke kollabiert und aus ihr letztendlich ein Stern entstehen kann. Handelt es sich bei der Gaswolke um eine protoplanetare Scheibe, kann das Jeans-Kriterium auch für die Entstehung von Gasplaneten herangezogen werden.

Während sich Gase unter irdischen Bedingungen in dem zur Verfügung stehenden Raum gleichmäßig ausbreiten, so werden dagegen größere Ansammlungen von Gasen im freien Weltall durch die Schwerkraft zusammengehalten und sind damit räumlich begrenzt.

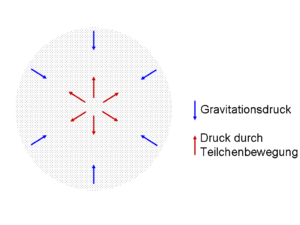
Die kinetische Energie der Gasmoleküle und die damit verbundenen Kollisionen der Moleküle treibt die Gaswolke auseinander, die Gravitation verhindert dagegen eine weitere Ausdehnung.

Das Jeans-Kriterium ist ein bedeutender Beitrag zur Theorie der Sternentstehung und geht von folgenden Bedingungen aus.

Es wird eine kugelförmige Gaswolke der Masse M und einer homogenen Dichte ρ, dem daraus zu berechnenden Radius R und der Temperatur T angenommen. Es wirken keine äußeren Kräfte auf diese Gaswolke und es findet auch keine Rotation der Wolke statt. Das Gas verhält sich wie ein ideales Gas.

Die Wolke beginnt zu kollabieren, falls die kontrahierenden Gravitationskräfte größer als die stabilisierende Kraft des Gasdruckes sind. Die Wolke zieht sich immer weiter zusammen, bis ein neuer Gleichgewichtszustand erreicht wird (Sternentstehung). Das Kriterium bestimmt die Masse (Jeans-Masse), ab der eine Kontraktion eintritt in Abhängigkeit von der Dichte, Masse und Temperatur der Gaswolke. Die Jean-Masse kann sowohl über der Gleichgewichtsdruck als auch über das Energiegleichgewicht formuliert werden.

Bei Gleichgewicht der Drücke im Zentrum der Wolke gilt:

$\ |p_{Gas}| = |p_{grav}|$.

Aus der idealen Gasgleichung $\ pV = nkT$ bzw. $\ p = \frac{\rho}{\mu}kT$ und dem Gravitationdruck im Inneren einer Kugel folgt als Gleichgewichtsbedingung

$\frac{\rho}{\mu}kT = \frac{3G M^2}{8\pi R^4}$,

wobei p der Druck, V das Volumen, n Zahl der Gasmoleküle, µ die Masse des einzelnen Gasmoleküls, k die Boltzmann-Konstante, T die absolute Temperatur und G die Gravitationskonstante sind.

Beim Ansatz über das Energiegleichgewicht ist die kinetische Energie $\ E_{kin} = \frac{3}{2} nkT$ entsprechend der Zustandsgleichung des idealen Gases so groß wie die gravitative Bindungsenergie der Gaswolke:

$\ E_{kin} = E_{grav}$

bzw. mit n = M/µ

$\frac{3}{2} \frac{M}{\mu}kT = \frac{3G M^2}{5R}$

Die Auflösung nach M führt mit $\ R = \sqrt[3]{\frac{3\, M}{4\, \pi\,\rho }}$ sowohl über die Druck- als auch Energiebedingung zu dem identischen Ergebnis der Jeans-Masse

$\ M = \left(\frac{6}{ \pi }\right)^{1/2}\cdot\left(\frac{k T}{G \mu}\right)^{3/2}\cdot \left(\frac{1}{\rho }\right)^{1/2}$

Dichte-Temperaturdiagramm für verschiedene Jeans-Massen (M) für ein einatomiges Wasserstoffgas

Die Jeans-Masse ist somit für kalte Gaswolken kleiner als für heiße, dafür aber bei niedrigen Gasdichten höher. Wird diese Masse bei gegebenen Bedingungen überschritten, kollabiert die Gaswolke. Das nebenstehende Diagramm gibt die Abhängigkeit verschiedner Jeans-Massen von der Dichte und der Temperatur wieder. Als Gas wurde einatomiges Wasserstoffgas als häufigstes Element im Universum gewählt (Masse pro Atom: µ ≈ 1,67 ∙ 10^-27 kg). Die Jeans-Masse ist als Vielfaches der Sonnenmasse angegeben.

Eine Wolke aus einatomigen Wasserstoffgas von beispielsweise 10 Sonnenmassen und einer Dichte von 10^-17kg•m^-3 kollabiert bei einer Temperatur von ≤ 10 K. Zur Veranschaulichung hätte eine solche Wolke etwa 6000 Atome pro cm³ und einen Durchmesser von 1,65 Lichtjahren (1,56 ∙ 10¹³ Kilometer).

Eine andere Ableitung von Jeans, ausgehend vom Durchmesser und Dichte der Wolke sowie der Schallgeschwindigkeit eines idealen Gases ergibt einen etwa vierfach größeren Vorfaktor im Vergleich zu dem obigen Ausdruck $\left(\frac{6}{ \pi }\right)^{1/2}$.

Literatur und Quellen

• Hermann Kolanoski: Einführung in die Astroteilchenphysik (PDF; 13,17 MB).
• Malcolm S. Longair: Galaxy Formation. Springer, Berlin u. a. 1998, ISBN 3-540-63785-0 (Astronomy and Astrophysics Library).
• Roman Sexl, Hannelore Sexl: Weiße Zwerge – Schwarze Löcher. Einführung in die relativistische Astrophysik. 2. erweiterte Auflage. Vieweg Verlag, Braunschweig u. a. 1999, ISBN 3-528-17214-2 (Vieweg-Studium – Grundkurs Physik).
• Albrecht Unsöld, Bodo Baschek: Der neue Kosmos. 4. völlig neubearbeitete Auflage. Springer, Berlin u. a. 1988, ISBN 3-540-18171-7.