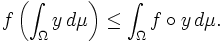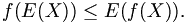- Jensen-Ungleichung
-
Die Jensensche Ungleichung ist eine elementare Ungleichung für konvexe und konkave Funktionen. Sie ist wegen ihrer Allgemeinheit Grundlage vieler bedeutender Ungleichungen, vor allem in der Analysis und Informationstheorie. Die Ungleichung ist nach dem dänischen Mathematiker Johann Ludwig Jensen benannt, der sie am 17. Januar 1905 bei einer Konferenz der Dänischen Mathematischen Gesellschaft präsentierte [1]. Unter etwas anderen Voraussetzungen findet sie sich bereits 1889 bei Otto Hölder [2].
Die Jensensche Ungleichung besagt, dass der Funktionswert einer konvexen Funktion an einer endlichen Konvexkombination von Stützstellen stets kleiner oder gleich einer endlichen Konvexkombination von den Funktionswerten der Stützstellen ist. Dies bedeutet insbesondere, dass das gewichtete arithmetische Mittel der Funktionswerte an n Stellen größer oder gleich dem Funktionswert am Mittel dieser n Stellen ist.
Inhaltsverzeichnis
Satz
Für eine konvexe Funktion
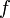 und für positive
und für positive 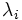 mit
mit 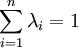 gilt:
gilt:Beweis per Induktion
Verwendet man die heute übliche Definition von konvex, dass
für alle reellen λ zwischen 0 und 1 gilt, so ergibt sich die jensensche Ungleichung einfach durch vollständige Induktion über die Anzahl der Stützstellen.
Beweis von Hölder
Hölder verwendete den Begriff konvex noch nicht und zeigte, dass aus
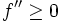 bzw.
bzw. 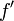 monoton steigend die Ungleichung
monoton steigend die Ungleichungfür positive
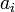 folgt, wobei er dies im Wesentlichen mit dem Mittelwertsatz der Differentialrechnung bewies.[2]
folgt, wobei er dies im Wesentlichen mit dem Mittelwertsatz der Differentialrechnung bewies.[2]Beweis von Jensen
Jensen ging von der schwächeren Definition
aus und zeigte unter ausdrücklichem Verweis auf den cauchyschen Beweis der Ungleichung vom arithmetischen und geometrischen Mittel mit vorwärts-rückwärts-Induktion, dass daraus die Beziehung
für beliebige natürliche Zahlen
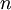 folgt. Daraus folgerte er dann weiter, dass
folgt. Daraus folgerte er dann weiter, dassfür natürliche Zahlen
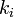 und somit
und somitfür beliebige rationale und, sofern
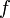 stetig ist, auch reelle Zahlen
stetig ist, auch reelle Zahlen 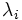 zwischen 0 und 1 mit
zwischen 0 und 1 mit 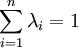 gilt.[1]
gilt.[1]Varianten
- Da für konkave Funktionen
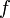 die Funktion
die Funktion 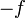 konvex ist, gilt für konkave Funktionen die jensensche Ungleichung in umgekehrter Richtung, d. h., für jede konkave Funktion
konvex ist, gilt für konkave Funktionen die jensensche Ungleichung in umgekehrter Richtung, d. h., für jede konkave Funktion 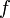 und für positive
und für positive 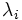 mit
mit 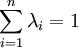 gilt:
gilt:
- Die stetige und die diskrete Variante lässt sich in der maßtheoretischen Variante zusammenfassen: Ist
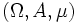 Maßraum mit
Maßraum mit 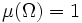 und ist
und ist 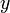 eine μ-integrierbare reellwertige Funktion, so gilt für jede im Bild von
eine μ-integrierbare reellwertige Funktion, so gilt für jede im Bild von 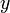 konvexe Funktion
konvexe Funktion 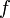 die Ungleichung
die Ungleichung
- Die jensensche Ungleichung ist z. B. für Erwartungswerte anwendbar. Ist
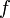 konvex und
konvex und 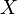 eine Zufallsvariable, dann gilt
eine Zufallsvariable, dann gilt
Anwendungen
Die jensensche Ungleichung lässt sich beispielsweise zum Beweis der Ungleichung vom arithmetischen und geometrischen Mittel und der Ky-Fan-Ungleichung verwenden.
Weblinks
Einzelnachweise
- ↑ a b Jensen, J. L. W. V. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. In Acta Math. 30, 175-193, 1906.
- ↑ a b O. Hölder Ueber einen Mittelwerthssatz. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen 1889, S 38ff.
Wikimedia Foundation.

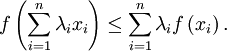
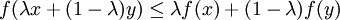
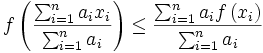
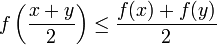
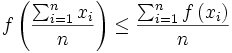
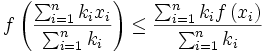
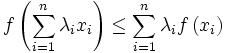
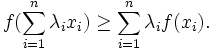
![y: [a,b]\to\R](/pictures/dewiki/101/e7654c1521ee5825fbf0c1cd7086c1f5.png) konvexe Funktion
konvexe Funktion