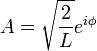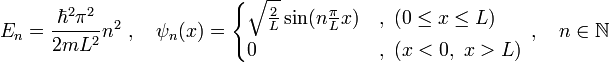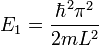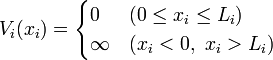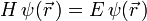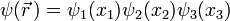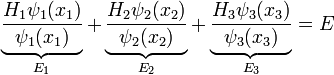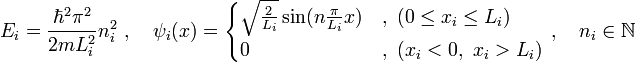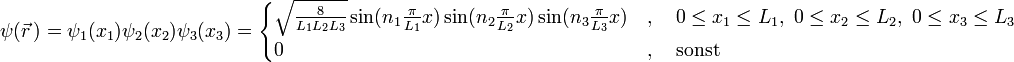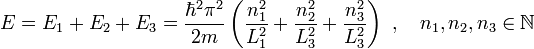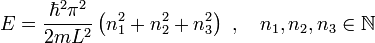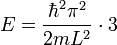- Kastenpotential
-
Das Teilchen im Kasten ist eines der verschiedenen Modellsysteme aus der Quantenmechanik, welches zur Quantisierung der Energie führt. In diesem Artikel soll die Schrödinger-Gleichung für diesen Modellfall gelöst werden.
Inhaltsverzeichnis
Gedanklicher Aufbau
Das eindimensionale Modellsystem besteht aus einem freien Teilchen (beispielsweise einem Gasmolekül), welches zwischen zwei "Wänden" (eine bei x = 0 und eine bei x = L) eingesperrt ist. Im Inneren des Kastens herrscht ein Potential von Null. Die "Wände" symbolisieren eine unendlich hohe Potentialbarriere. Im Gegensatz zur klassischen Physik führt die quantenmechanische Beschreibung dieses Modells zu zwei wesentlichen Unterschieden:
- Es sind nur Teilchen zugelassen, deren Wellenlänge zwischen die Wände passt.
- An den Wänden muss die Wellenfunktion Null sein. (Diese Randbedingung begründet sich aus mathematischen Forderungen für die Schrödinger-Gleichung.)
Wenn die Potentialbarriere endlich ist, kommt ein dritter Unterschied hinzu. Ein quantenmechanisches Teilchen kann auch eine Potentialbarriere überwinden, für die es eigentlich nicht genügend Energie besitzt. Dies nennt man den Tunneleffekt.
Die Lösungen der Schrödinger-Gleichung führen zur Quantisierung der Energie
Der Hamiltonoperator des eindimensionalen Problems lautet in Ortsdarstellung
geht mit dem Ansatz
in die zeitunabhängige (stationäre) Schrödingergleichung über.
Im Folgenden wird die zeitunabhängige Schrödingergleichung zu lösen sein (Eigenwertproblem des Hamiltonoperators)
Innerhalb des Kastens
Die stationäre Schrödingergleichung entspricht innerhalb des Kastens der eines freien Teilchens (gewöhnliche Differentialgleichung 2. Ordnung)
Für die Wellenfunktion ψ(x) innerhalb des Kastens wählt man folgenden Ansatz
Äquivalent wäre der Ansatz mit komplexen Exponentialfunktionen ψ(x) = Aexp(ikx) + Bexp( − ikx).
Diesen Ansatz setzt man in die Schrödingergleichung ein, wobei die zweite Ableitung nach dem Ort
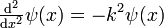 ist.
ist.Somit erhält man die Energie E in Abhängigkeit von der Wellenzahl k:
Außerhalb des Kastens, Stetigkeitsbedingung
Außerhalb des Kastens muss die Wellenfunktion aufgrund des unendlich hohen Potentials identisch Null sein.
Da die Wellenfunktion jedoch überall stetig sein muss, werden somit Randbedingungen an die Wellenfunktion im Kasten gestellt, nämlich dass die Wellenfunktion
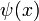 an den Wänden gleich 0 ist:
an den Wänden gleich 0 ist: .
.
Randbedingung 1
Aus der ersten Randbedingung folgt für die Wellenfunktion innerhalb des Kastens
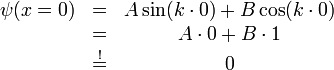 .
.
Damit diese Gleichung erfüllt wird, muss B = 0 sein. Damit vereinfacht sich die Wellenfunktion zu
 .
.
Randbedingung 2
Mit Hilfe der zweiten Randbedingung folgt dann für die Wellenfunktion innerhalb des Kastens
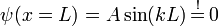 .
.
Damit diese Gleichung erfüllt wird, muss kL ein ganzes Vielfaches von π sein, also
Somit darf die Wellenzahl k nur diskrete Werte annehmen
Eigentlich folgt aus der zweiten Randbedingung nur, dass
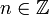 eine ganze Zahl ist. Für n = 0 wäre allerdings die Wellenfunktion
eine ganze Zahl ist. Für n = 0 wäre allerdings die Wellenfunktion 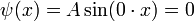 überall Null und somit die Normierungsbedingung nicht zu erfüllen, also ist n = 0 nicht erlaubt. Für negative
überall Null und somit die Normierungsbedingung nicht zu erfüllen, also ist n = 0 nicht erlaubt. Für negative 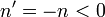 ist die Wellenfunktion bis auf das Vorzeichen dieselbe wie für das positive n, nämlich
ist die Wellenfunktion bis auf das Vorzeichen dieselbe wie für das positive n, nämlich 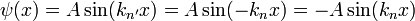 . Da Wellenfunktionen, die sich um einen Faktor unterscheiden, denselben Zustand beschreiben, bringen die negativen ganzen Zahlen keine neuen Zustände hervor. Deshalb beschränkt man sich auf
. Da Wellenfunktionen, die sich um einen Faktor unterscheiden, denselben Zustand beschreiben, bringen die negativen ganzen Zahlen keine neuen Zustände hervor. Deshalb beschränkt man sich auf 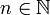
Wie oben berechnet, hängt die Energie E von der Wellenzahl k ab, einsetzten liefert:
Da n nur ganzzahlige Werte annehmen darf, kann die Energie ebenfalls nur bestimmte Werte annehmen. Die Energie des Teilchens ist somit gequantelt, die Energieniveaus sind „diskret“.
Normierung
Die Amplitude A lässt sich noch über die Normierungsbedingung bestimmen:
Da A eine komplexe Zahl ist, ist nur ihr Betrag festgelegt, die Phase
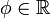 ist beliebig:
ist beliebig:Wellenfunktionen, die sich nur um einen konstanten Phasenfaktor unterscheiden beschreiben denselben Zustand. Deshalb kann man φ = 0 setzen und somit
 reell wählen.
reell wählen.Zusammenfassung
Die Eigenwerte (= mögliche Energiewerte) und Eigenfunktionen (= Wellenfunktionen) des Hamiltonoperators für ein Teilchen im Kasten mit unendlich hohen Potentialwänden sind also:
Grundzustand
Die Grundzustandsenergie ist nicht Null (n = 0 ist nicht erlaubt), sondern
Dies erhält man auch aus der Betrachtung der Heisenbergschen Unschärferelation
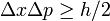 : Das Teilchen ist auf den Raumbereich xmax = L eingeschränkt. Dann ergibt sich der minimale Impuls über xmaxpmin = h / 2. Innerhalb des Kastens ist das Potential gleich Null, somit ist die Gesamtenergie gleich der kinetischen Energie E = p2 / 2m.
: Das Teilchen ist auf den Raumbereich xmax = L eingeschränkt. Dann ergibt sich der minimale Impuls über xmaxpmin = h / 2. Innerhalb des Kastens ist das Potential gleich Null, somit ist die Gesamtenergie gleich der kinetischen Energie E = p2 / 2m.Dreidimensionaler Fall
Im dreidimensionalen Kasten (Quader) sieht der Hamiltonoperator wie folgt aus:
Dabei ist das Potential
Den vollständigen Hamiltonoperator kann man mittels
als Summe dreier eindimensionaler Hamiltonoperator schreiben:
- H = H1 + H2 + H3
Separationsansatz
Die stationäre Schrödingergleichung (dreidimensional)
lässt sich mit folgendem Produktansatz
in drei eindimensionale Probleme separieren.
Setze dazu den Produktansatz in die stationäre Schrödingergleichung ein und nutze aus, dass Hi nur auf ψi wirkt, d. h. die anderen ψj kann man am Hamiltonoperator vorbeiziehen.
Teilen durch ψ1(x1)ψ2(x2)ψ3(x3) liefert:
Dabei wurden die drei Separationskonstanten E1, E2, E3 definiert, deren Summe die Gesamtenergie E ergibt:
- E = E1 + E2 + E3
Eindimensionale Probleme
Nun muss für jede Raumrichtung separat das eindimensionales Problem, wie oben bereits geschehen, gelöst werden:
Deren Lösung ist:
Gesamtlösung
Die Lösung des dreidimensionalen Kastens ist für die Gesamtwellenfunktion das Produkt der eindimensionalen Wellenfunktionen
und für die Gesamtenergie die Summe der eindimensionalen Energieeigenwerte:
Entartung
Für einen Würfel, also L1 = L2 = L3 ist die Energie gegeben durch:
Die Energieeigenwerte können entartet sein, d. h. unterschiedliche Quantenzahlen führen auf dieselbe Energie. Das bedeutet hier, dass unterschiedliche Quantenzahlen n1,n2,n3 zu derselben Summe
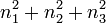 führen.
führen.Der niedrigste Energiewert ist nicht entartet (= einfach entartet) n1 = n2 = n3 = 1:
Der nächsthöhere Energiewert ist bereits dreifach entartet:
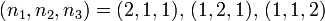 somit
somit 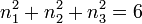 :
:Es können auch höhere Entartungen als dreifach auftreten, z.B. 4-fach
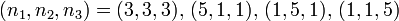 somit
somit 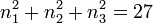 .
.Modell für konjugierte Systeme
Das Teilchen im Kasten kann als einfaches Modell für ein konjugiertes Molekül, z.B. Hexatrien, verwendet werden, um dessen Energie abzuschätzen. Man nimmt an, dass sich die Elektronen in einem konjugierten Molekül in diesem frei bewegen können, aber es nicht verlassen können. Man addiert formal ein halbes Atom an jedem Ende des Moleküls. Die Länge dieses Teilchens entspricht dann dem Kasten in dem sich das Elektron befindet.
Beispiele
Ein Beispiel aus der Kristallographie ist das Farbzentrum, bei denen ein Elektron in einer Anionen-Leerstelle eingesperrt ist und das sich in guter Näherung als ein Teilchen im Kasten beschreiben lässt. Auch die Farbigkeit von Farbstoffen mit linearen konjugierten Pi-Systemen lässt sich erfassen, indem man das Pi-System als 1-dimensionales Teilchen im Kasten-Problem betrachtet.
Siehe auch
Wikimedia Foundation.


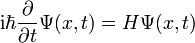
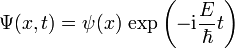
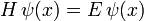
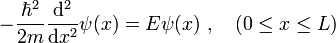
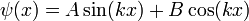
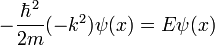
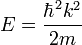
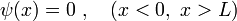
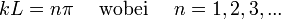

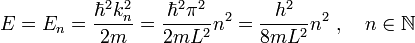
![1\overset{!}{=}\int_{\mathbb{R}}\psi_{n}^{*}(x)\psi_{n}(x)=|A|^{2}\int_{0}^{L}\sin^{2}(n\frac{\pi}{L}x)\mathrm{d}x=|A|^{2}\left[\frac{x}{2}-\frac{L}{4n\pi}\sin\left(2n\frac{\pi}{L}x\right)\right]_{0}^{L}=|A|^{2}\left(\frac{L}{2}-\frac{L}{4n\pi}\underbrace{\sin\left(2n\pi\right)}_{=0}\right)=|A|^{2}\frac{L}{2}](/pictures/dewiki/52/488119b7699c338e95f32a6cefc5e724.png)