Kleiner Satz von Picard

Die Sätze von Picard (nach Charles Émile Picard) sind Sätze der Funktionentheorie, eines Teilgebietes der Mathematik.

Sie lauten wie folgt:

• Der Kleine Satz von Picard besagt, dass das Bild jeder nicht-konstanten ganzen Funktion die gesamte komplexe Zahlenebene ist, aus der höchstens ein Punkt herausgenommen wurde.

• Der Große Satz von Picard besagt, dass eine Funktion mit einer wesentlichen Singularität in jeder noch so kleinen Umgebung dieser Singularität jeden komplexen Wert mit höchstens einer Ausnahme unendlich oft annimmt.

Bemerkungen:

• In beiden Sätzen ist die eventuelle „Ausnahme eines Punktes“ offenbar nötig. Zum Beispiel bildet 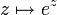$z\mapsto e^z$ nicht auf 0 ab, ebenso ist 0 nicht im Bild von 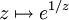$z\mapsto e^{1/z}$ einer jeden punktierten Umgebung von 0 enthalten.

• Der Kleine Satz folgt sofort aus dem Großen Satz, denn eine ganze Funktion ist entweder ein Polynom oder sie hat eine wesentliche Singularität in $\infty$.

• Der Große Satz verallgemeinert den Satz von Weierstraß-Casorati.

• Eine Vermutung von Bernhard Elsner^[1] ist mit dem Großen Satz von Picard verwandt: Sei 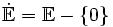$\dot{\mathbb{E}}=\mathbb{E}-\{0\}$ die punktierte offene Einheitskreisscheibe und 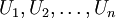$U_1,U_2,\dots,U_n$ eine endliche offene Überdeckung von 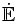$\dot{\mathbb{E}}$. Auf jedem U_j sei eine schlichte (d.h. injektive holomorphe) Funktion f_j gegeben, so dass df_j = df_k auf jeder Schnittmenge 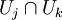$U_j\cap U_k$. Dann verschmelzen die Differentiale zu einer meromorphen 1-Form auf der Einheitskreisscheibe 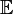$\mathbb{E}$. (Im Fall, dass das Residuum verschwindet, folgt die Vermutung aus dem Großen Satz.)

Einzelnachweise

1. ↑ Ann. Inst. Fourier 49-1 (1999) p.330