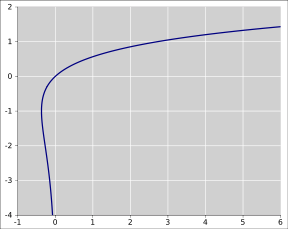
Lambertsche W-Funktion

Der Graph von W(x) für W > −4 und x < 6. Der obere Zweig W ≥ −1 ist die Funktion W₀ (principal branch), der untere Zweig mit W ≤ −1 ist die Funktion W₋₁.

In der Mathematik ist die lambertsche W-Funktion (oder Lambert-W-Funktion), auch Omegafunktion, benannt nach Johann Heinrich Lambert, die Umkehrfunktion von

$f(x):= x e^x,\,$

wobei e^x die Exponentialfunktion ist. Die lambertsche W-Funktion wird meistens mit W(x) bezeichnet. Es gilt

$z = W(z)e^{W(z)}, z\in\mathbb C.$

Eigenschaften

Da die Funktion f auf dem Intervall $\left(-\infty,0\right]$ nicht injektiv ist, besitzt die lambertsche W-Funktion auf dem Intervall $\left[-\tfrac 1e,0\right)$ zwei Funktionsäste W₀(x) und W _{− 1}(x). Mit W(x) wird aber in der Regel der obere der Äste bezeichnet. Die W-Funktion kann nicht als elementare Funktion ausgedrückt werden. Zumeist wird sie in der Kombinatorik verwendet, beispielsweise zur Auswertung von Bäumen oder zur asymptotischen Bestimmung der Bell-Zahlen. Die Ableitungsfunktion der W-Funktion kann mit Hilfe des Satzes über die Ableitung der Umkehrfunktion gefunden werden:

$W'(x)=\frac{W(x)}{x(1+W(x))}.$

Die Ableitungen höherer Ordnung haben die Form

$\frac{\mathrm{d}^n W(x)}{\mathrm{d}x^n}=\frac{(-1)^{n+1} W^n(x)}{x^n (1+W(x))^{2n-1}}\cdot P_n(W(x)),$

wobei die P_n Polynome sind, welche sich aus folgender Rekursionsformel berechnen lassen:

$P_{n+1}(t) = (n t+ 3n-1)\cdot P_n(t)-(t+1)\cdot P_n'(t), \quad n \ge 1.$

Ausgehend von P₁(t) = 1 ergeben sich damit die nächsten drei Ableitungen zu:

$W''(x)\,\,=-\frac{W^2(x)}{x^2 (1+W(x))^3}\cdot (W(x)+2),$

$W^{(3)}(x)=+\frac{W^3(x)}{x^3 (1+W(x))^5}\cdot (2W^2(x)+8W(x)+9),$

$W^{(4)}(x)=-\frac{W^4(x)}{x^4 (1+W(x))^7}\cdot (6W^3(x) +36W^2(x) +79W(x) +64).$

Eine Stammfunktion ergibt sich durch Substitution des gesamten Integranden:

$\int W(x)\, \mathrm dx = x \left(W(x) - 1 + \frac 1{W(x)} \right) + C.$

Durch implizite Differentiation kann man zeigen, dass W folgender Differentialgleichung genügt:

$z(1+W)\frac{\mathrm dW}{\mathrm dz}=W\quad\text{mit }z\neq -\frac 1e.$

Die Taylor-Reihe von W in x₀ = 0 ist gegeben durch

$W(x) = \sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}\ x^n = x - x^2 + \frac 32 x^3 - \frac 83 x^4 + \frac{125}{24}x^5 - \dotsb.$

Der Konvergenzradius beträgt $\tfrac 1e$.

Spezielle Werte

$W\left(-\frac{\pi}{2}\right) = \frac{\mathrm i\pi} 2$

$W\left(-\frac 1e\right) = -1$

$W\left(-\frac{\ln 2}{2}\right)= -\ln 2$

$W\left(0\right) = 0$

$W\left(1\right) = 0{,}5671432904... = \Omega$   (die Omega-Konstante^[1])

$W\left(e\right) = 1$

Eigenschaften

• $\int_{0}^{\pi} W\left( 2\cot^2(x) \right)\sec^2(x)\,\mathrm dx = 4\sqrt{\pi}$

• $\int_{0}^{+\infty} W\left(\frac{1}{x^2}\right)\,\mathrm dx = \sqrt{2\pi}$

• $\int_{0}^{+\infty} \frac{W(x)}{x\sqrt{x}}\,\mathrm dx = 2\sqrt{2\pi}$

Verwendung außerhalb der Kombinatorik

Die lambertsche W-Funktion kann gebraucht werden, um Gleichungen vom Typus

$\, a(x)e^{a(x)}=y$

zu lösen (a(x) ist ein beliebiger, von x abhängiger Ausdruck).

Auch die Gleichung

$\, x^x=z$

kann mit Hilfe der lambertschen W-Funktion gelöst werden. Die Lösung lautet

$x=\frac{\ln z}{W(\ln z)}=\exp\left(W(\ln z)\right).$

Der infinite (unendliche) Potenzturm

$\operatorname{expturm}(x):=x^{x^{x^{\cdot^{\cdot^{\cdot}}}}}$

kann an den konvergenten Stellen mit der W-Funktion in geschlossene Form gebracht werden, was auch die Ableitung ermöglicht:

$\operatorname{expturm}(x)=\frac{W(-\ln x)}{-\ln x}.$

Verallgemeinerungen

Mit Hilfe der normalen lambertschen W-Funktion lassen sich die exakten Lösungen „transzendenter algebraischer“ Gleichungen (in x) folgender Form ausdrücken:

$e^{-c x} = a_0 (x-r) ~~\quad\qquad\qquad\qquad\quad(1)$

wobei a₀, c und r reelle Konstanten sind. Die Lösung ist $x = r + \frac{1}{c} W \left( \frac{c e^{-c r}}{a_0 } \right)$. Verallgemeinerungen der lambertschen W-Funktion^[2] umfassen:

• Eine Anwendung auf dem Gebiet der allgemeinen Relativitätstheorie und der Quantenmechanik (Quantengravitation) in niedrigeren Dimensionen, die eine zuvor unbekannte Verknüpfung zwischen beiden Gebieten aufzeigte, siehe Journal of Classical and Quantum Gravity,^[3] wobei die rechte Seite von (1) nun ein quadratisches Polynom in x ist:

$e^{-c x} = a_0 (x-r_1 ) (x-r_2 ) ~~\qquad\qquad(2)$

Hierbei sind r₁ und r₂ voneinander verschiedene reelle Konstanten, die Wurzeln des quadratischen Polynoms. Die Lösung ist eine Funktion allein des Arguments x, aber r_i und a₀ sind Parameter dieser Funktion. Insofern ähnelt diese Verallgemeinerung der hypergeometrischen Funktion und der Meijer G-Funktion, aber sie gehört zu einer anderen "Klasse" von Funktionen. Wenn r₁ = r₂, so können beide Seiten von (2) faktorisiert und auf (1) reduziert werden, so dass sich die Lösung auf die normale lambertsche W-Funktion reduziert. Gl. (2) entspricht der Gleichung für das „Dilaton“-Feld, von welchem die Metrik des „linealen“ Zwei-Körper-Gravitationsproblems in 1+1 Dimensionen (eine räumliche und eine zeitliche Dimension) für den Fall ungleicher (Ruhe-)Massen abgeleitet ist, sowie dem Problem der Eigenwertberechnung für das quantenmechanische Doppelminimum-Dirac-Deltafunktions-Modell in einer Dimension und mit „ungleichen“ Ladungen.

• Analytische Lösungen der Energie-Eigenwerte für einen speziellen Fall des quantenmechanischen Analogons des Eulerschen Drei-Körper-Problems, nämlich des (drei-dimensionalen) Wasserstoffmolekül-Ions.^[4] Hier ist nun die rechte Seite von (1) (oder (2)) das Verhältnis von zwei Polynomen unendlicher Ordnung in x:

$e^{-c x} = a_0 \frac{\prod_{i=1}^{\infty} (x-r_i )}{ \prod_{i=1}^{\infty} (x-s_i)} \qquad \qquad\qquad(3)$

wobei r_i und s_i unterschiedliche reelle Konstanten sind, und x ist eine Funktion des Energie-Eigenwertes und des Kern-Kern-Abstands R. Gl. (3), mit den Spezialfällen (1) und (2), steht in Beziehung zu einer großen Klasse retardierter Differentialgleichungen. Die Anwendungen der lambertschen W-Funktion auf grundlegende physikalische Probleme sind damit selbst für die normale lambertsche W-Funktion, siehe (1), keineswegs erschöpft. Dies zeigen jüngste Beispiele aus dem Gebiet der Atom-, Molekül-, und optischen Physik.^[5]

Numerische Berechnung

Eine Folge von Näherungen an die W-Funktion kann rekursiv mithilfe der Beziehung

$w_{j+1}=w_j-\frac{w_j e^{w_j}-z}{e^{w_j}(w_j+1)-\frac{(w_j+2)(w_je^{w_j}-z)}{2w_j+2}}$

berechnet werden^[6] Oder auch mit:

$w_{j+1}=w_j-\frac{w_j e^{w_j}-z}{e^{w_j}+e^{w_j} w_j}$.

Tabelle reeller Funktionswerte

W₀, oberer Zweig:

$\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} x & -0.3679 & -0.34 & -0.2& 0&0.3&0.7&1.2&2&3&4&6&10&20&40\\ \hline y &-1 &-0.6537 & -0.2592 & 0&0.2368&0.4475&0.6356&0.8526&1.0499&1.2022&1.4324&1.7455&2.205&2.6968\\ \end{array}$

W _{− 1}, unterer Zweig:

$\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} x & -0.3679 & -0.365 & -0.355& -0.31&-0.25&-0.18&-0.1&-0.05&-0.025&-0.01&-0.005&-0.001&-0.0001&0\\ \hline y &-1 &-1.1307 & -1.2912 & -1.7044&-2.1533&-2.7128&-3.5772&-4.4998&-5.3696&-6.4728&-7.284&-9.118&-11.6671&-\infty\\ \end{array}$

Andere Werte lassen sich leicht über $x = y\, e^y$ berechnen.

Eine Näherung von W₀(x) für grosse x ist^[7]

$\,W_0(x) \approx \ln(x)-\ln(\ln(x))+\ln(\ln(x))/\ln(x).$

Einzelnachweise

1. ↑ Omega constant in der englischsprachigen Wikipedia
2. ↑ T.C. Scott, R.B. Mann: General Relativity and Quantum Mechanics: Towards a Generalization of the Lambert W Function. In: AAECC (Applicable Algebra in Engineering, Communication and Computing), 17 no. 1, April 2006. p.41–47. acm.org; Arxiv-Artikel
3. ↑ P.S. Farrugia, R.B. Mann, T.C. Scott: N-body Gravity and the Schrödinger Equation. In: Class. Quantum Grav. 24, 2007, p. 4647–4659. iop.org; Arxiv-Artikel
4. ↑ T.C. Scott, M. Aubert-Frécon, J. Grotendorst: New Approach for the Electronic Energies of the Hydrogen Molecular Ion. In: Chem. Phys. 324: 2006. p.323–338. sciencedirect.com; Arxiv-Artikel
5. ↑ T.C. Scott, A. Lüchow, D. Bressanini, J.D. Morgan III: The Nodal Surfaces of Helium Atom Eigenfunctions. In: Phys. Rev. A, 75:060101, 2007. scitation.aip.org
6. ↑ Corless et al.: On the Lambert W function. In: Adv. Computational Maths. 5, 1996, p. 329–359
7. ↑ Eric Weisstein, "Lambert W-Function." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/LambertW-Function.html