Lemniskatischer Sinus

Sinus lemniscatus sl (schwarz) und Cosinus lemniscatus cl (blau), zum Vergleich der auf sl normierte Sinus (hellgrau)

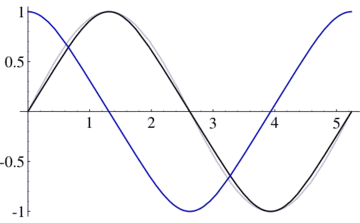
Der lemniskatische Sinus oder sinus lemniscatus (kurz sinlemn oder sl), ist eine spezielle, von dem Mathematiker Carl Friedrich Gauß eingeführte mathematische Funktion. Der lemniskatische Sinus entspricht derjenigen Funktion für die Lemniskate, die der Sinus für den Kreis ist. Der lemniskatische Cosinus (kurz coslemn oder cl) leitet sich direkt von sl ab. Beides sind die historisch ersten, heute so genannten elliptischen Funktionen.

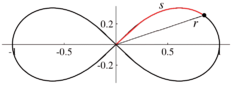
Der 19jährige Gauß beschäftigte sich 1796 (in erst nach seinem Tod veröffentlichten Notizen) mit der Frage, wie man aus einer gegebenen Bogenlänge s einer Lemniskate den Abstand $r\in(-1,1)$ des entsprechenden Punktes auf der Kurve vom Koordinatenursprung r = 0 berechnen kann. Mathematisch führt das auf die Umkehrfunktion r = r(s) des elliptischen Integrals

$s(r) = \int_0^r \frac{\mathrm{d}\,\rho}{\sqrt{1-\rho^4}}.$

Gauß nannte diese Umkehrfunktion Sinus lemniscatus und bezeichnete sie mit "sl", also

$r = \mathrm{sl}\,s$

Die Länge s des Lemniskatenbogens hängt ab von dem Abstand r des Kurvenpunktes zum Ursprung

Entsprechend definierte er den Cosinus lemniscatus $\mathrm{cl}\,s = \mathrm{sl}\,(\omega - s)$, wobei ω die Länge des Halbbogens der Lemniskate ist, also

$\omega = \int_0^1 \frac{\mathrm{d}\,\rho}{\sqrt{1-\rho^4}} \approx 1{,}31103.$

Gauß ließ sich bei diesen Bezeichnungen von der Analogie zu den Kreisfunktionen leiten, denn der Sinus ist die Umkehrfunktion des Integrals

$s(r) = \int_0^r \frac{\mathrm{d}\,\rho}{\sqrt{1-\rho^2}}, \qquad \mbox{und}\qquad \omega = \int_0^1 \frac{\mathrm{d}\,\rho}{\sqrt{1-\rho^2}} = \frac{\pi}{2}.$

also r = sin s und $\cos s = \sin({\textstyle \frac\pi2} - s)$. Seine weitere entscheidende Idee war es nun, die Funktionen sl und cl nicht nur für reelle Zahlen zu definieren, sondern sie ins Komplexe fortzusetzen. Er bewies dann die Periodizitätsrelationen

$\mathrm{sl}\,(s + 4\omega) = \mathrm{sl}\,s, \qquad \mathrm{sl}\,(s + 4\mathrm{i}\omega) = \mathrm{sl}\,s.$

Im Gegensatz zum Sinus hat also der lemniskatische Sinus sl zwei Perioden 4ω und 4iω, ebenso die Funktion cl. Die lemniskatischen Funktionen sind also elliptisch. Carl Gustav Jacobi führte um 1830 die jacobischen elliptischen Funktionen ein und verallgemeinerte damit die beiden lemniskatischen Funktionen.

Siehe auch

• Lemniskatische Konstante

Literatur

• E. D. Solomentsev: Lemniscate functions. In: Michiel Hazewinkel (Hrsg.): Encyclopaedia of Mathematics. Springer-Verlag, Berlin 2002, ISBN 1-4020-0609-8.

Weblinks

• Eric W. Weisstein: Lemniscate Function. In: MathWorld. (englisch)