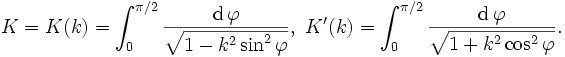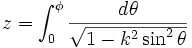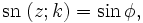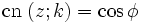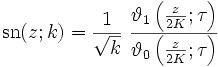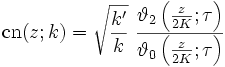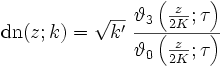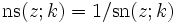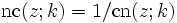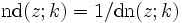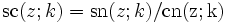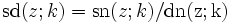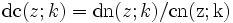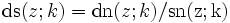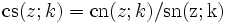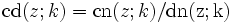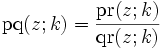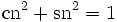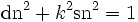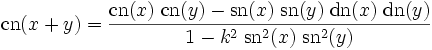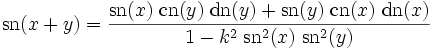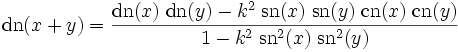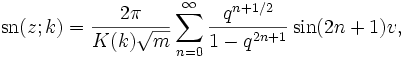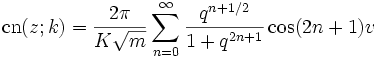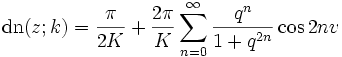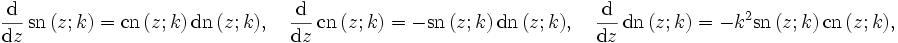- Delta amplitudinis
-
In der Mathematik ist eine Jacobische elliptische Funktion eine von zwölf speziellen elliptischen Funktionen. Die Jacobischen elliptischen Funktionen haben einige Analogien zu den trigonometrischen Funktionen und finden zahlreiche Anwendungen in der mathematischen Physik, bei elliptischen Filtern und in der Geometrie, insbesondere für die Pendelgleichung und die Bogenlänge einer Ellipse. Carl Gustav Jakob Jacobi führte sie um 1830 ein. Carl Friedrich Gauß hatte jedoch schon 1796 mit dem lemniskatischen Sinus und Cosinus zwei spezielle Jacobische Funktionen untersucht, seine Notizen darüber aber nicht veröffentlicht. Für die allgemeine Theorie der elliptischen Funktionen spielen heute jedoch weniger die Jacobischen als vielmehr die Weierstraßschen elliptischen Funktionen eine Rolle.
Die drei grundlegenden Jacobischen Funktionen
Es gibt zwölf Jacobische elliptische Funktionen, von denen sich neun aus drei grundlegenden Funktionen bilden lassen. Gegeben sei ein Parameter k, der elliptische Modul, der der Ungleichung 0 < k < 1 genügt. Er wird oft auch als m angegeben, wobei m = k2, oder als modularer Winkel α, wobei sin2α = k2. Daneben werden oft die sogenannten komplementären Parameter
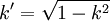 sowie m1 = k'2 verwendet. Die drei grundlegenden Jacobischen elliptischen Funktionen sind dann:
sowie m1 = k'2 verwendet. Die drei grundlegenden Jacobischen elliptischen Funktionen sind dann:- der sinus amplitudinis
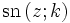 ,
, - der cosinus amplitudinis
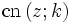 ,
, - das delta amplitudinis
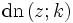 .
.
Sie sind elliptische Funktionen und haben dementsprechend zwei Perioden. Insgesamt gelten für sie die folgenden Eigenschaften:
Funktion Perioden Nullstelle Polstelle 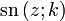
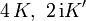
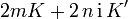
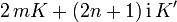
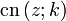
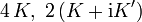
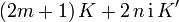
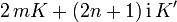
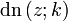
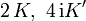
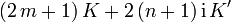
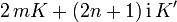
n und m sind ganze Zahlen Hierbei hängen die Perioden K und K' mit dem Parameter k zusammen über die elliptischen Integrale
So hat sn beispielsweise Nullstellen bei z = 0 und z = 2K, sowie Polstellen bei
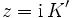 und
und 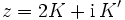 .
.Speziell für
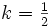 ergeben der Sinus amplitudinis bzw. der Cosinus amplitudinis, bis auf eine Konstante, die von Gauß eingeführten lemniskatischen Sinus- und Cosinusfunktionen,
ergeben der Sinus amplitudinis bzw. der Cosinus amplitudinis, bis auf eine Konstante, die von Gauß eingeführten lemniskatischen Sinus- und Cosinusfunktionen,Für die Grenzwerte k = 0 und k = 1 ergeben die Jacobi-Funktionen (nichtelliptischen) trigonometrischen Funktionen bzw. Hyperbelfunktionen:
Funktion k=0 k=1 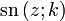
sinz tanhz 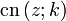
cosz 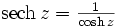
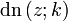
1 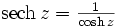
Definitionen
Es gibt mehrere äquivalente Definitionen der Jacobischen Funktionen.
Abstrakte Definition als spezielle meromorphe Funktionen
Gegeben seien als freie Parameter der elliptische Modul k mit 0 < k < 1 und die wie oben davon abhängenden reellen Zahlen K und K' , mit
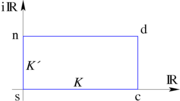
Ferner sei ein Rechteck mit den Seitenlängen K und K' in der komplexen Ebene mit den Ecken s, c, d, n gegeben, dessen Ecke s im Ursprung liege und die Seitenlängen K und K' habe. Die Seiten der Länge K seien dabei parallel zur reellen Achse, die der Länge K' parallel zur imaginären Achse. Die Ecke c sei der Punkt K, d der Punkt K + iK' und n der Punkt iK' auf der imaginären Achse. Die zwölf Jacobischen elliptischen Funktionen bilden sich dann aus einer Buchstabenkombination pq, wobei p
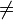 q jeweils einer der Buchstaben s, c, d, n sind.
q jeweils einer der Buchstaben s, c, d, n sind.Eine Jacobische elliptische Funktion
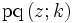 ist dann die eindeutige doppelt-periodische meromorphe Funktion, die die folgenden drei Eigenschaften erfüllt:
ist dann die eindeutige doppelt-periodische meromorphe Funktion, die die folgenden drei Eigenschaften erfüllt:- Die Funktion
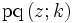 hat bei p eine einfache Nullstelle und bei q eine einfache Polstelle.
hat bei p eine einfache Nullstelle und bei q eine einfache Polstelle. - Die Funktion
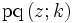 ist periodisch in Richtung p–q, wobei die Periode die doppelte Entfernung von p nach q ist. Ähnlich ist
ist periodisch in Richtung p–q, wobei die Periode die doppelte Entfernung von p nach q ist. Ähnlich ist 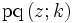 periodisch in den beiden anderen Richtungen, jedoch mit einer Periode, die dem Vierfachen der Entfernung von p zu dem anderen Punkt entspricht.
periodisch in den beiden anderen Richtungen, jedoch mit einer Periode, die dem Vierfachen der Entfernung von p zu dem anderen Punkt entspricht. - Wird die Funktion
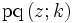 um den Eckpunkt p entwickelt, so lautet der führende Term einfach z (mit dem Koeffizienten 1), der führende Term der Entwicklung um den Punkt q ist 1/z, und der führende Term der Entwicklung um die beiden anderen Eckpunkte ist jeweils 1.
um den Eckpunkt p entwickelt, so lautet der führende Term einfach z (mit dem Koeffizienten 1), der führende Term der Entwicklung um den Punkt q ist 1/z, und der führende Term der Entwicklung um die beiden anderen Eckpunkte ist jeweils 1.
Definition als Umkehrfunktionen elliptischer Integrale
Die obige Definition als eindeutige meromorphe Funktion ist sehr abstrakt. Äquivalent kann eine Jacobische elliptische Funktion als eindeutige Umkehrfunktion des unvollständigen elliptischen Integrals erster Art definiert werden. Dies ist die übliche und vielleicht verständlichste Definition. Sei k ein gegebener Parameter mit 0 < k < 1, und sei
also z = z(φ). Dann sind die Jacobischen elliptischen Funktionen sn, cn und dn gegeben durch
und
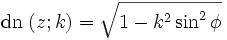 .
.
Der Winkel φ = φ(z) ist dabei die Amplitude, für
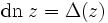 heißt er Delta-Amplitude. Ferner genügt der freie Parameter k der Ungleichung
heißt er Delta-Amplitude. Ferner genügt der freie Parameter k der Ungleichung 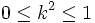 . Für φ = π / 2 ist z die Viertelperiode K.
. Für φ = π / 2 ist z die Viertelperiode K.Die anderen neun Jacobischen elliptischen Funktionen werden aus diesen drei grundlegenden gebildet, siehe nächsten Abschnitt.
Definition mit Hilfe der Theta-Funktionen
Eine weitere Definition der Jacobi-Funktionen verwendet die Thetafunktionen. Seien k und k' zwei reelle Konstanten mit 0 < k,k' < 1 und k2 + k'2 = 1. Dann lauten die drei grundlegenden Jacobischen Funktionen
Dabei gilt
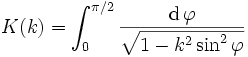 ,
,
K'(k) = K(k') und τ = iK'(k) / K(k).
Die abgeleiteten Jacobi-Funktionen
Üblicherweise werden die Kehrwerte der drei grundlegenden Jacobi-Funktionen durch die Umkehrung der Buchstabenreihenfolge bezeichnet, also:
Die Verhältnisse der drei grundlegenden Jacobi-Funktionen werden durch den jeweils ersten Buchstaben des Zählers und des Nenners bezeichnet, also:
Verkürzt können wir also schreiben
wobei p, q und r jeweils einer der Buchstaben s, c, d, n sind und ss = cc = dd = nn = 1 gesetzt wird.
Additionstheoreme
Die Jacobi-Funktionen genügen den beiden algebraischen Beziehungen
Somit parametrisieren (cn, sn, dn) eine elliptische Kurve, die die Schnittmenge der beiden durch die obigen Gleichungen definierten Quadriken darstellt. Ferner können wir mit den Additionstheoremen ein Gruppengesetz für Punkte auf dieser Kurve definieren:
Quadratische Beziehungen
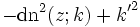
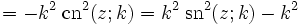
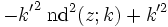
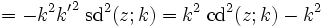
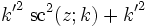
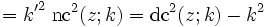
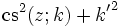
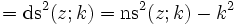
mit k2 + k'2 = 1. Weitere quadratische Beziehungen können mit
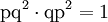 und
und 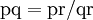 gebildet werden, wobei p, q und r jeweils einer der Buchstaben s, c, d, n sind und ss = cc = dd = nn = 1 gesetzt wird.
gebildet werden, wobei p, q und r jeweils einer der Buchstaben s, c, d, n sind und ss = cc = dd = nn = 1 gesetzt wird.Entwicklung als Lambert-Reihe
Mit q = exp( − πK' / K) (auf engl. nome) und dem Argument v = πu / (2K(k)) können die Funktionen in eine Lambert-Reihe entwickelt werden,
und
Die elliptischen Jacobi-Funktionen als Lösungen nichtlinearer Differentialgleichungen
Die Ableitungen der drei grundlegenden elliptischen Jacobi-Funktionen lauten
Mit den obigen Additionstheoremen sind sie für ein gegebenes k mit 0 < k < 1 daher Lösungen der folgenden nichtlinearen Differentialgleichungen:
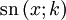 löst die Differentialgleichungen
löst die Differentialgleichungen 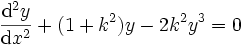 und
und 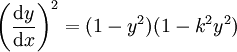
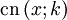 löst die Differentialgleichungen
löst die Differentialgleichungen 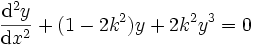 und
und 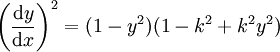
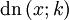 löst die Differentialgleichungen
löst die Differentialgleichungen 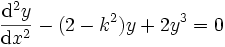 und
und 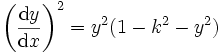
Verwandte Themen
Weblinks
- Definition in Abramowitz & Stegun (engl.)
- Eric W. Weisstein: Jacobi Elliptic Functions. (Mathworld) (engl.)
Literatur
- Heinrich Durège: Theorie der elliptischen Functionen. B. G. Teubner, Leipzig 1861.
- Charles Hermite: Uebersicht der Theorie der elliptischen Funktionen. Wiegandt & Hempel, Berlin 1863.
- Carl Gustav Jakob Jacobi: C. G. J. Jacobi's gesammelte Werke. G. Reimer, Berlin 1881–1891
- Leo Koenigsberger: Vorlesungen über die Theorie der elliptischen Functionen, nebst einer Einleitung in die allgemeine Functionenlehre. B. G. Teubner, Leipzig 1874.
- Karl Weierstrass: Formeln und Lehrsätze zum Gebrauche der elliptischen Functionen. W. Fr. Kaestner, Göttingen 1883–1885.
- Robert Fricke: Die elliptischen Funktionen und ihre Anwendungen, Teil 2. B.G. Teubner, Leipzig 1922.
- Milton Abramowitz and Irene Stegun: Handbook of Mathematical Functions. Dover Publications, New York 1964. ISBN 0-486-61272-4. (Chapter 16)
- Naum Iljitsch Achieser: Elements of the Theory of Elliptic Functions, Moscow 1970, translated into English as AMS Translations of Mathematical Monographs, Volume 79, AMS, Rhode Island 1990. ISBN 0-8218-4532-2
- E. T. Whittaker and G. N. Watson: A Course of Modern Analysis, Cambridge University Press, 1940, 1996. ISBN 0521588073
- E. Zeidler (Hrsg.): Teubner-Taschenbuch der Mathematik, Teubner, Stuttgart / Leipzig 1996. ISBN 3-8154-2001-6
- der sinus amplitudinis
Wikimedia Foundation.