Löbs Paradox

Currys Paradoxon, auch Löbs Paradoxon, ist ein Paradoxon der naiven Mengenlehre und der meisten Logiken. Es erlaubt die Herleitung einer beliebigen Aussage aus einem selbstbezüglichen Ausdruck mittels einfacher logischer Regeln. Es ist benannt nach dem Logiker Haskell Curry bzw. nach dem Mathematiker Martin Hugo Löb.

Das Paradoxon in natürlicher Sprache

Eine Version des Paradoxons in natürlicher Sprache lautet beispielsweise wie folgt:

Wenn dieser Satz wahr ist, dann gibt es den Weihnachtsmann.

Nehmen wir zunächst an, der Satz sei nicht wahr. Damit ist die gestellte Bedingung („Wenn dieser Satz wahr ist...“) offensichtlich nicht erfüllt, und eine Aussage über die Existenz des Weihnachtsmannes ist mit diesem Satz wegen der nicht erfüllten Bedingung nicht möglich.

Von einem generellen Standpunkt aus betrachtet, ist jedoch eine solche Aussage („Wenn irgendetwas ganz sicher nicht Wahres gelten würde, dann gäbe es auch den Weihnachtsmann“) andererseits aus logischer Sicht eine wahre Aussage; sie enthält keinen Widerspruch. Somit führt unsere anfängliche Annahme, der Satz sei nicht wahr, dazu, dass der Satz eine wahre Aussage ist; also, dass der Satz wahr ist.

Das ist ein Widerspruch, denn ein Satz kann nicht unwahr sein (gemäß unserer Annahme) und zugleich wahr (gemäß der genannten logischen Folgerungen). Also muss unsere ursprüngliche Annahme („Nehmen wir zunächst an, der Satz sei nicht wahr“) falsch sein. Mit anderen Worten: Der Satz muss von vornherein wahr sein. Und da er aussagt, dass, wenn er selbst wahr ist, auch der Weihnachtsmann existiert, so schließen wir, dass der Weihnachtsmann tatsächlich existiert. (Dieser logische Schritt folgt im Rahmen der Systeme natürlichen Schließens.)

Daraus folgt: Ist der Satz wahr, so gibt es den Weihnachtsmann. Das ist aber genau die Aussage des Satzes (auch ohne die anfängliche Annahme, dass er wahr ist), also ist der Satz wahr und der Weihnachtsmann existiert.^[1]

Da man statt der Behauptung „Es gibt den Weihnachtsmann“ jede beliebige Aussage auf diese Weise beweisen kann, handelt es sich um ein Paradoxon.

Das Paradoxon in der mathematischen Logik

Sei Y die zu beweisende Aussage, beispielsweise Y = "Es gibt den Weihnachtsmann". Sei ferner X der Satz, dass Y aus dem Wahrsein von X folgt. Mathematisch kann man das als den formalen Ausdruck X = (X → Y) schreiben, X ist also als Term von sich selbst definiert. Dann lautet der Beweis:

1. X → X

Tautologie

2. X → (X → Y)

ersetze die rechte Seite von 1, da X = (X → Y)

3. X → Y

folgt aus 2 mit Kontraktion

4. X

ersetze 3, da X = (X → Y)

5. Y

aus 4 und 3 mit modus ponens

Ein Spezialfall des Paradoxons ergibt sich, wenn Y einen Widerspruch der Form Z∧¬Z darstellt. Dann lautet der Satz X = (X → (Z∧¬Z)). Setzt man den Satz vom Widerspruch voraus, so folgt aus (X → (Z∧¬Z)) sofort ¬X. Setzt man weiter das Ex falso quodlibet voraus, so folgt mit ¬X, dass aus X jede beliebige Aussage folgt, insbesondere X → Z∧¬Z. Also ist X → Z∧¬Z äquivalent zu ¬X, d. h. X = ¬X. Dies ist genau das Lügner-Paradoxon.

Das Paradoxon in der naiven Mengenlehre

Um das Paradoxon zu vermeiden, könnte man selbstbezügliche Sätze in der zugrunde liegenden mathematischen Logik verbieten. Allerdings kann man in Mengenlehren, die das Aussonderungsaxiom (vgl. Zermelo-Fraenkel-Mengenlehre) nicht voraussetzen, ebenfalls eine beliebige logische Aussage Y aus der Menge

$X \ \stackrel{\mathrm{def}}{=}\ \left\{ x | ( x \in x ) \to Y \right\}.$

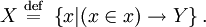
folgern. Der Beweis lautet:

$\begin{matrix} \mbox{1.} & ( X \in X ) \iff ( ( X \in X ) \to Y ) & \mbox{(Definition von } X) \\ \mbox{2.} & ( X \in X ) \to ( ( X \in X ) \to Y ) & \mbox{(aus 1)} \\ \mbox{3.} & ( X \in X ) \to Y & \mbox{(aus 2, Kontraktion)} \\ \mbox{4.} & ( ( X \in X ) \to Y) \to ( X \in X ) & \mbox{(aus 1)} \\ \mbox{5.} & X \in X & \mbox{(aus 3 und 4, modus ponens)} \\ \mbox{6.} & Y & \mbox{(aus 3 und 5, modus ponens)} \end{matrix}$

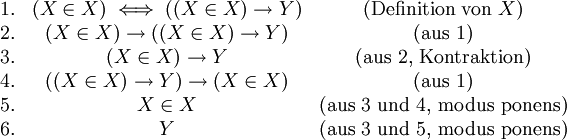
Ein Spezialfall dieses Paradoxons ist, wenn Y ein Widerspruch ist. Dann ergibt sich 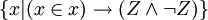$\left\{ x | ( x \in x ) \to ( Z \wedge \neg Z ) \right\}$, was äquivalent zu 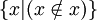$\left\{ x | ( x \notin x ) \right\}$ ist, der Menge aller Mengen, die sich nicht selbst enthalten. Das ist genau Russells Paradoxon.

Diskussion

Currys Paradox kann in jeder Sprache formuliert werden, die die folgenden Bedingungen erfüllt:

1. Die Sprache besitzt einen Mechanismus, der Selbstbezüglichkeit zulässt, beispielsweise Anführungszeichen oder Ausdrücke wie „Dieser Satz“.
2. Die Sprache besitzt ein Wahrheitsprädikat: die Sprache, z. B. „L“, enthält ein Prädikat „wahr-in-L“ und kann es jedem beliebigen Satz zuschreiben.
3. Die Sprache erlaubt die „Kontraktionsregel“, die grob gesprochen besagt, dass eine relevante Hypothese mehrfach verwendet werden kann.
4. Die Sprache erlaubt die Tautologie „wenn A, dann A“ und den Modus ponens (aus „A“ und „wenn A dann B“ schließe „B“).

Natürliche Sprachen haben diese Eigenschaften. Die mathematische Logik andererseits ermöglicht zwar nicht notwendig die explizite Selbstbezüglichkeit, allerdings zeigt der Gödelsche Unvollständigkeitssatz, dass sie in genügend reichen Sprachen (z. B. mit der Gödelnummer) stets konstruierbar ist. Das Wahrheitsprädikat ist ebenfalls nicht immer verfügbar, in der naiven Mengenlehre jedoch erhält man es durch die Aussonderungsregel. Der Kettenschluss wird allgemein akzeptiert, allerdings besitzt die lineare Logik (genauer, die lineare Logik ohne Exponentialoperatoren) nicht die notwendigen Schlussregeln für das Paradoxon.

Anders als das Lügner-Paradoxon oder Russells Antinomie ist Currys Paradoxon unabhängig von der Negation der Logik, da diese in seiner Formulierung nicht verwendet wird. Daher existiert es auch in parakonsistenten Logiken, die immun gegen das Lügner-Paradoxon sind.

Die Auflösung von Currys Paradoxon ist umstritten, da nichttriviale Auflösungen (wie das Verbot selbstbezüglicher Sätze) viel vom Sprachreichtum nehmen und nicht intuitiv sind. Die Logiker sind uneins, ob und wie solche Sätze eingeschränkt gelten oder gar bedeutungslos sind, oder ob das Paradoxon sogar ernsthafte Probleme mit dem Begriff der Wahrheit selbst offenlegt.

Literatur

Curry, H.: „The inconsistency of certain formal logics“, Journal of Symbolic Logic 7, pp. 115–117 (1942)

Quellen

1. ↑ George S. Boolos, John P. Burgess, Richard C. Jeffrey: Computability And Logic, 4th edition, Cambridg University Press 2002, Cambridge, ISBN 9780521007580, S. 237

Weblinks

• Stanford Encyclopedia of Philosophy: „Curry’s Paradox“ – von J. C. Beall (engl.).
• Grossman, Jason, University of Sydney History & Philosophy of Science: A Proof that Penguins Rule the Universe. Kurze unterhaltsame Diskussion von Currys Paradoxon.