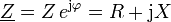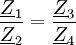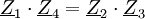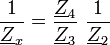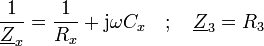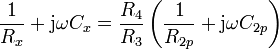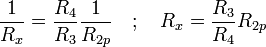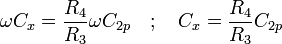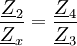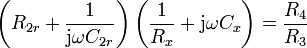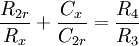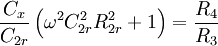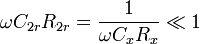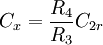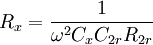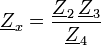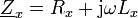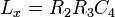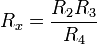Maxwell-Wien-Brücke

Mit einer Wechselspannungsbrücke können in der elektrischen Messtechnik die Kapazitätswerte von Kondensatoren und die Induktivitätswerte von Spulen gemessen werden. Darüber hinaus werden Wechselspannungsbrücken zu verschiedenen anderen Aufgaben eingesetzt, z. B. als phasendrehende Schaltung.

Passive lineare Bauteile unter Wechselspannung

Ein realer Kondensator wird durch eine (ideale) Kapazität und einen ohmschen Widerstand angenähert beschrieben, die in einem Ersatzschaltbild in Parallelschaltung oder Reihenschaltung angeordnet sind. Entsprechendes gilt für die Spule mit Induktivität und ohmschem Widerstand.

Die Bauteile bilden in einem Wechselstromkreis komplexe Widerstände Z . Deren Größe kann man angeben durch Betrag Z und Phasenverschiebungswinkel φ oder durch Real- und Imaginärteil

$\underline Z =Z\,e^{\mathrm j \varphi} =R+\mathrm j X$

Bei einer Induktivität L ist 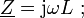$\underline Z = \mathrm j \omega L\ ;$ bei einer Kapazität C ist $\underline Z = \frac{1}{\mathrm j \omega C}$ .

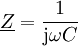Dabei steht ω = 2πf für die Kreisfrequenz und f für die Frequenz der anliegenden sinusförmigen Wechselspannung; j steht für die imaginäre Einheit mit $\mathrm j=\sqrt{-1}$ .

Grundschaltung einer Wechselspannungs-Messbrücke

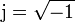Prinzip der Messbrücke

Die Wechselspannungsbrücke ist aufgebaut wie eine Wheatstone-Brücke, siehe nebenstehendes Schaltbild. Sie benötigt eine Wechselspannungsquelle zur Speisung und ein für Wechselspannung empfindliches Messgerät zur Bestimmung der Brückenquerspannung; die vier Widerstände dürfen komplex sein. Die Brücke wird als abgeglichen bezeichnet, wenn die Querspannung gleich null ist, obwohl die Amplitude der Speisespannung größer null ist. In diesem Fall ist

$\frac{\underline Z_1}{\underline Z_2} =\frac{\underline Z_3}{\underline Z_4}$

oder

$\underline Z_1 \cdot \underline Z_4 =\underline Z_2 \cdot \underline Z_3$

Um diese komplexe Abgleichbedingung zu erfüllen, müssen die

Betragsbedingung 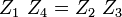$Z_1\ Z_4=Z_2\ Z_3$ und die

Winkelbedingung 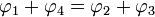$\varphi_1 +\varphi_4 =\varphi_2 +\varphi_3\$ erfüllt sein.

Ob eine Brücke überhaupt abgleichbar ist, erkennt man daran, ob die Winkelbedingung erfüllbar ist.

Bei einer abgeglichenen Brücke berechnet man den Messwert damit, dass die komplexe Abgleichbedingung in Real- und Imaginärteil erfüllt sein muss.

Zur Einstellung des Abgleichs sind zwei veränderbare Bauteile erforderlich. In der Regel müssen diese mehrmals abwechselnd iterativ eingestellt werden. Je nach Schaltung gibt es frequenzunabhängige und frequenzabhängige Lösungen. Bei letzteren kann die Brückenquerspannung nicht auf null, sondern nur auf ein Minimum gebracht werden, wenn die Speisespannung Oberschwingungsanteile enthält.

Unter den vielen entwickelten Wechselspannungs-Messbrücken haben sich zwei Arten besonders bewährt; sie werden nachfolgend beschrieben.

Wechselspannungsmessbrücke zur Messung einer Kapazität

Wien-Brücke

Diese Brücke eignet sich zur Messung einer Kapazität. In nebenstehendem Schaltbild liegt der auszumessende, im Allgemeinen verlustbehaftete Kondensator auf der Position von 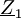$\underline Z_1$ und wird hier dargestellt im Parallel-Ersatzschaltbild.

Mit der komplexen Abgleichbedingung in der Form

$\frac{1}{\underline Z_x} =\frac{\underline Z_4 }{\underline Z_3 }\ \frac{1}{\underline Z_2}$

und

$\frac{1}{\underline Z_x} =\frac{1}{R_x} +\mathrm j \omega C_x \quad ;\quad \underline Z_3 = R_3$

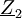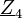und entsprechend für $\underline Z_2$ und $\underline Z_4$ gemäß Schaltung, erhält man

$\frac{1}{R_x} +\mathrm j \omega C_x =\frac{R_4}{R_3} \left (\frac{1}{R_{2p}} +\mathrm j \omega C_{2p} \right)$

Realteil:

$\frac{1}{R_x}=\frac{R_4}{R_3} \frac{1}{R_{2p}} \quad ; \quad R_x =\frac{R_3}{R_4} R_{2p}$

Imaginärteil:

$\omega C_x =\frac{R_4}{R_3}\omega C_{2p} \quad ; \quad C_x =\frac{R_4}{R_3} C_{2p}$

Wechselspannungsmessbrücke zur Messung einer Kapazität mit geringem Verlust

Bei Kondensatoren mit hoher Güte bzw. geringem Verlust kann R_2p einen sehr hohen Wert annehmen, der schwer einstellbar ist. Im Grenzfall eines idealen Kondensators geht R_2p → ∞ . Für die Messung an solchen Bauteilen wird auf der Position von Z ₂ statt der Parallelschaltung eine Reihenschaltung verwendet, bei der der ohmsche Widerstand R_2r einen kleinen Wert annimmt, im idealen Grenzfall R_2r → 0. Diese Schaltung wird auch im Rückkopplungszweig des Wien-Brücken Oszillators verwendet^[1]. Die mathematische Behandlung hierzu ist schwieriger, und das Ergebnis ist frequenzabhängig. Mit der komplexen Abgleichbedingung in der Form

$\frac{\underline Z_2}{\underline Z_x} =\frac{\underline Z_4}{\underline Z_3}$

und $\underline Z_2 = R_{2r} +\frac{1}{\mathrm j \omega C_{2r}}$

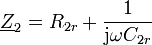
erhält man

$\left(R_{2r} +\frac{1}{\mathrm j \omega C_{2r}}\right) \left(\frac{1}{R_x} +\mathrm j \omega C_x\right) =\frac{R_4}{R_3}$

Realteil:

$\frac{R_{2r}}{R_x} +\frac{C_x}{C_{2r}} = \frac{R_4}{R_3}$

Imaginärteil:

$\omega C_x R_{2r} =\frac{1}{\omega C_{2r} R_x} \quad ;\quad \omega C_{2r} R_{2r} =\frac{1}{\omega C_x R_x}$

Durch Eliminierung von R_x erhält man eine Gleichung für C_x

$\frac{C_x}{C_{2r}} \left(\omega^2 C_{2r}^2 R_{2r}^2 +1 \right) =\frac{R_4}{R_3}$

Eine Kapazität mit geringem Verlust ist im Parallel-Ersatzschaltbild gekennzeichnet durch 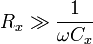$R_x \gg \frac{1}{\omega C_x}$ . Dann wird

$\omega C_{2r} R_{2r} =\frac{1}{\omega C_x R_x} \ll 1$

und die Gleichung für C_x vereinfacht sich zu

$C_x = \frac{R_4}{R_3} C_{2r}$

In dieser Näherungslösung entfällt die Frequenzabhängigkeit. Anders ist das bei der Kennzeichnung des Verlustes. In dieser Schaltung ergibt sich unabhängig von der Näherung

$R_x=\frac{1}{\omega ^2 C_x C_{2r}R_{2r}}$

Wechselspannungsmessbrücke zur Messung einer Induktivität

Maxwell-Wien-Brücke

Eine der Wien-Brücke entsprechende Schaltung zur Messung einer Induktivität mit einer zweiten Induktivität ist die Maxwell-Brücke. Diese liefert allerdings keine hochwertigen Ergebnisse, da

1. keine Spulen zur Verfügung stehen, die in ihrer Induktivität zu Vergleichszwecken hinreichend genau bekannt sind,
2. Spulen durch ihre Leitungswiderstände in höherem Maße verlustbehaftet sind.

Beide Nachteile werden in der Maxwell-Wien-Brücke vermieden, die als Referenzbauteil einen Kondensator verwendet. In nebenstehendem Schaltbild liegt die auszumessende verlustbehaftete Spule auf der Position von 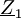$\underline Z_1$ und wird hier dargestellt im Reihen-Ersatzschaltbild.

Mit der komplexen Abgleichbedingung in der Form

$\underline Z_x =\frac{\underline Z_2\,\underline Z_3} {\underline Z_4}$

und

$\underline Z_x =R_x +\mathrm j \omega L_x$

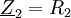$\underline Z_2 =R_2$ usw. gemäß Schaltung

erhält man aus dem Imaginärteil der Abgleichbedingung die Induktivität

$L_x=R_2R_3C_4\$

und aus dem Realteil den ohmschen Verlustwiderstand

$R_x=\frac{R_2R_3}{R_4}\$

Siehe auch

Wien-Robinson-Brücke, Schering-Brücke

Quellen/Referenzen

1. ↑ http://www.e-technik1.uni-rostock.de/deutsch/edu/schalt2/wienbr.pdf