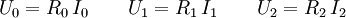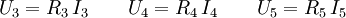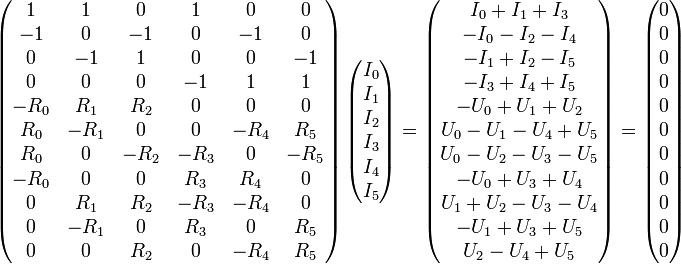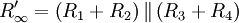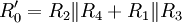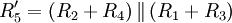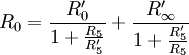Meßbrücke

Brückenschaltung mit Spannungsquelle.

Eine Brückenschaltung, auch H-Schaltung, H-Brücke oder Vollbrücke genannt, ist eine elektrische Schaltung, bei der in der Grundform fünf Zweipole in Form des Großbuchstabens H zusammengeschaltet sind. Die Querverbindung heißt Brückenzweig.

Prinzip

Eine Brückenschaltung aus Widerständen kann man als Parallelschaltung zweier Spannungsteiler interpretieren, zwischen deren Ausgangsklemmen der Brückenzweig liegt. Der Vorteil der Brückenschaltung gegenüber einem einzelnen Spannungsteiler besteht darin, dass man die Spannung und den Strom im Brückenzweig je nach Einstellung der Widerstände nicht nur in der Höhe sondern auch in der Polarität verändern kann.

Hierbei wird bei Brückenschaltungen zwischen Viertel- (ein Widerstand variabel), Halb- (zwei Widerstände variabel) und Vollbrücken (vier Widerstände variabel) unterschieden.

Das Messobjekt – ein Widerstand oder eine andere Impedanz – ist Teil des Spannungsteilers auf der einen Seite. Mindestens ein weiteres Teil wird variabel ausgeführt, so dass ein Nullabgleich des Stroms (bzw. des Spannungsunterschieds) im Brückenzweig durchgeführt werden kann, der eine besonders präzise Werteermittlung erlaubt, da ein Nulldurchgang wesentlich genauer bestimmt werden kann als ein Extremum. Das Messinstrument im verbindenden Brückenzweig kann üblicherweise zwischen negativen und positiven Werten unterscheiden und liefert damit auch einen Hinweis, in welcher Richtung geändert werden muss. Der Abgleich erfolgt so lange, bis das Instrument so exakt wie möglich eine Nullanzeige liefert. Dazu ist das Instrument bei manchen Messbrücken in seiner Empfindlichkeit umschaltbar, so dass man von einem Grob- zum Feinabgleich wechseln kann. Die Impedanz des Messobjekts wird durch die Einstellung des verstellbaren Brückenglieds angezeigt (oder aus dessen angezeigtem Wert berechnet).

Nur zur Messung rein ohmscher Widerstände kann man die Messbrücke mit Gleichspannung betreiben. Zur Messung von Impedanzen (Spulen oder Kondensatoren) ist ein Betrieb mit Wechselspannung notwendig, der auch für ohmsche Widerstände günstig sein kann. Nicht notwendig, aber hilfreich ist in diesen Fällen die Anzeige der Phasenlage, um die Richtung der Verstimmung anzuzeigen. Siehe auch bei Wechselspannungsbrücke.

Verwendet man nicht einen Nullabgleich, sondern das Ausschlagverfahren, dann kann aus Betrag und Phase der Diagonalspannung die Impedanz berechnet werden. So können auch die (äquivalenten) Verlustwiderstände von Spulen oder Kondensatoren bestimmt werden, ohne dass diese im anderen Brückenzweig nachgebildet werden müssen.

Berechnung

Eine Brückenschaltung kann am besten durch die Kirchhoffschen Regeln beschrieben werden. Dazu stellt man zuerst die Knoten- und Maschengleichungen auf. Optional kann man die daraus hergeleiteten Zusammenhänge auch in einer Matrixgleichung darstellen. Eine besondere Herausforderung ist hierbei die Berechnung des Gesamtschaltungswiderstandes wie dies später erläutert wird.

Aufstellen der Knoten- und Maschengleichungen

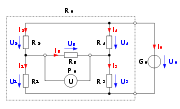
Beim Aufstellen der Knoten- und Maschengleichungen gehen wir in diesem Beispiel von der Annahme aus, dass die Ströme in Richtung des Spannungspfeils fließen. Ist diese Annahme für einen Strom falsch, so ergibt sich für den Betrag des jeweiligen Stromes ein negatives Vorzeichen, wodurch sich jedoch nicht die Gültigkeit der Gleichungen ändert. Aus den Kirchoffschen Regeln resultieren schließlich die folgenden Knotengleichungen:

+ I₀ + I₁ + I₃ = 0

− I₀ − I₂ − I₄ = 0

− I₁ + I₂ − I₅ = 0

− I₃ + I₄ + I₅ = 0

Durch die Maschenregel erhält man die folgenden Gleichungen:

− U₀ + U₁ + U₂ = 0

+ U₀ − U₁ − U₄ + U₅ = 0

+ U₀ − U₂ − U₃ − U₅ = 0

− U₀ + U₃ + U₄ = 0

+ U₁ + U₂ − U₃ − U₄ = 0

− U₁ + U₃ + U₅ = 0

+ U₂ − U₄ + U₅ = 0

Hierbei sind die Gleichungen nicht vollständig linear unabhängig, weshalb man eine Gleichung weglassen kann.

Zusätzlich gilt für die einzelnen Widerstände der Zusammenhang

$\left\{ U_n=R_n\,I_n \left| n\in \mathbb{N} \land n \in \left[ 0,5 \right] \right.\right\}$

oder ausgeschrieben:

$U_0=R_0\,I_0\qquad U_1=R_1\,I_1\qquad U_2=R_2\,I_2$

$U_3=R_3\,I_3\qquad U_4=R_4\,I_4\qquad U_5=R_5\,I_5$

Hierbei stellt der Widerstand R₀ den Widerstand der Schaltung aus der Sicht der Spannungsquelle dar.

Matrixdarstellung der Knoten- und Maschengleichungen

Die Matrixdarstellung ist eine Hilfe bei großen Gleichungssystemen und daher insbesondere bei großen Schaltungen. Um die Matrixdarstellung zu ermitteln setzt man für die einzelnen Spannungen das jeweilige Produkt aus Widerstand und Strom ein. Daraus erhält man:

$\begin{pmatrix} 1& 1& 0& 1& 0& 0\\ -1& 0& -1& 0& -1& 0\\ 0& -1& 1& 0& 0& -1\\ 0& 0& 0&-1& 1& 1 \\-R_0& R_1& R_2& 0 & 0 & 0 \\ R_0&-R_1& 0 & 0 &-R_4& R_5 \\ R_0& 0 &-R_2&-R_3& 0 &-R_5 \\-R_0& 0 & 0 & R_3& R_4& 0 \\ 0 & R_1& R_2&-R_3&-R_4& 0 \\ 0 &-R_1& 0 & R_3& 0 & R_5 \\ 0 & 0 & R_2& 0 &-R_4& R_5 \end{pmatrix}\, \begin{pmatrix}I_0\\I_1\\I_2\\I_3\\I_4\\I_5\end{pmatrix} = \begin{pmatrix} I_0+I_1+I_3\\ -I_0-I_2-I_4\\ -I_1+I_2-I_5\\ -I_3+I_4+I_5\\ -U_0+U_1+U_2\\ U_0-U_1-U_4+U_5\\ U_0-U_2-U_3-U_5\\ -U_0+U_3+U_4\\ U_1+U_2-U_3-U_4\\ -U_1+U_3+U_5\\ U_2-U_4+U_5\\ \end{pmatrix} = \begin{pmatrix} 0\\0\\0\\0\\0\\0\\0\\0\\0\\0\\0 \end{pmatrix}$

Die Matrixdarstellung wird bevorzugt zur Verwendung in Computeralgebrasystemen oder in Schaltungssimulatoren verwendet, da etwa mit dem Gauß- und dem Gauß-Jordan-Algorithmus, sowie der Cramer'schen Regel, effiziente Lösungsalgorithmen existieren. Im gegebenen Beispiel ist die Cramer'sche Regel jedoch nur auf eine Teilmatrix anwendbar, da die Determinante der linken Matrix aufgrund der oberen vier Reihen immer Null sein würde.

Berechnung des Schaltungswiderstandes

Die Berechnung von R₀ kann anhand der über die Kirchoffschen Regeln aufgestellten Beziehungen erzielt werden. Eine schnellere Variante stellt die folgende Vorgehensweise dar:

1. Zuerst wird 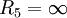$R_5=\infty$ angenommen, wodurch eine Unterbrechung entsteht. Dadurch ergibt sich die Gleichung:

   $R'_\infty=\left(R_1+R_2\right)\|\left(R_3+R_4\right)$

2. Anschließend wird R₅ = 0 gesetzt und dadurch kurzgeschlossen. Dadurch erhält man die Gleichung:

   $R'_0=R_2\|R_4+R_1\|R_3$

3. Nun ermittelt man den Widerstand aus Sicht von R₅, wobei die Spannungsquelle unendlich gesetzt wird:

   $R'_5=\left(R_2+R_4\right)\|\left(R_1+R_3\right)$

4. Dies kann man in die folgende Gleichung einsetzen, welche vorab mit Hilfe der durch die Kirchhoffschen Regeln ermittelten Formeln und Vereinfachung ermittelt wurde:

   $R_0=\frac{R'_0}{1+\frac{R_5}{R'_5}} + \frac{R'_\infty}{1+\frac{R'_5}{R_5}}$

Alternativ und mit weniger Rechenaufwand, lässt sich R' auch mit Hilfe der Stern-Dreieck-Transformation berechnen. Dazu werden R1,R3, bzw. R2, R4 sowie R5, durch ihr Sternäquivalent ersetzt. Dadurch ergibt sich eine einfache Schaltung mit je 2 Reihenwiderständen parallel und das ganze in Reihe mit einem 5. Widerstand.

Abgleichbedingung

Eine Brückenschaltung wird als abgeglichen bezeichnet, wenn I₅ = 0 und damit kein Strom des einen Brückenzweigs in den anderen fließt. Ist dies der Fall, gilt

$I_L = I_1 = I_2;\quad I_R = I_3 = I_4$.

Daraus folgt der Zusammenhang

$\frac{U_1}{U_2}=\frac{U_3}{U_4} \Leftrightarrow \frac{U_2}{U_1}=\frac{U_4}{U_3} \Leftrightarrow\frac{I_L\,R_1}{I_L\,R_2}=\frac{I_R\,R_3}{I_R\,R_4} \Leftrightarrow\frac{R_1}{R_2}=\frac{R_3}{R_4} \Leftrightarrow R_1\,R_4 = R_2\,R_3$.

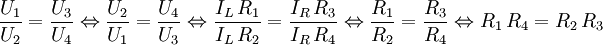Anwendungen

Die Brückenschaltung dient unter anderem als Grundlage für folgende Schaltungen:

Energietechnik bzw. Leistungselektronik

• Der Brückengleichrichter wandelt Wechselstrom in Gleichstrom um.
• Schaltbrücken (Vollbrücke, Halbbrücke) werden in Schaltnetzteilen, Motorsteuerungen und Frequenzumrichtern verwendet.
• Vierquadrantensteller
• Endstufen von Audioverstärker sind meist als Halbbrücke ausgeführt, können aber auch als Vollbrücke (BTL von engl. Bridge Teminated Load) ausgebildet sein.

Messtechnik

• Die Wheatstonesche Messbrücke dient zur Bestimmung mittlerer ohmscher Widerstände.
• Die Thomson-Brücke ist zur Messung kleiner ohmscher Widerstände geeignet.
• Mit der Wien-Brücke können Kapazitäten gemessen werden, mit der Maxwell-Brücke oder besser der Maxwell-Wien-Brücke Induktivitäten.
• Die Wien-Robinson-Brücke dient zur Frequenzmessung.
• Die Schering-Brücke wird zur Bestimmung der Kapazität und des Verlustfaktors von Kondensatoren, vorwiegend in der Hochspannungstechnik, eingesetzt.
• Brückenschaltungen mit Dehnmessstreifen zur Kraft- oder Druckmessung siehe unter Wheatstonesche Messbrücke.

Nachrichtentechnik

• Ringmodulatoren ähneln im Schaltungsaufbau Brückengleichrichtern, dienen aber zur Modulation von Signalen.