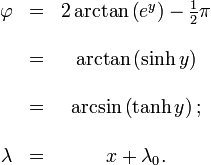Mercatorprojektion

Mercator-Projektion – die Polargebiete erscheinen enorm vergrößert.

Die Mercator-Projektion in der Kartografie leitet sich aus der Zylinderprojektion ab, wobei die Projektion entlang der Zylinderachse – also in Nord-Süd-Richtung – geeignet verzerrt ist, um eine winkeltreue Abbildung zu erreichen. Gleichzeitig wird aber eine starke Flächenverzerrung in den Polarregionen in Kauf genommen. Insbesondere die Schifffahrt benutzt in den Seekarten diese winkelkorrigierte Darstellung der Erdoberfläche zur Navigation.

Sie wurde nach ihrem Erfinder, dem Kartografen Gerhard Mercator benannt, der dem damaligen Zeitgeist entsprechend seinen Namen Gerhard Kremer latinisiert hatte.

Aufbau

Um die Erde wird ein Zylinder gelegt, der diese am Äquator berührt. Vom Projektionszentrum in der Erdmitte werden nun alle Punkte vom Globus auf den Zylinder übertragen. Rollt man danach den Zylinder ab, so erhält man eine flache Karte der Erdoberfläche. Dies ist noch keine Mercator-Projektion, denn die Bogenlängen der Breitengrade sind zwar streckentreu, aber die Bogenlängen der Längengrade sind dies nicht und werden vom Äquator aus in Nord-Süd-Richtung wachsend gestreckt dargestellt; die Abbildung ist also noch nicht winkeltreu. Um Winkeltreue herzustellen, wird die Karte in Nord-Süd-Richtung verzerrt. Im Abbildungsgesetz, welche geographische Breite in welchem Abstand vom Äquator in der Karte abgebildet wird, tritt bei dieser Korrektur anstelle des Tangens der geographischen Breite eine andere Funktion, nämlich das Integral des Kehrwertes des Cosinus.

Abbildungseigenschaft

Da der Äquator die Berührungslinie von Zylinder und Globus ist, wird dieser längentreu abgebildet. Zum Nord- und Südpol hin werden die Verzerrungen immer größer. Dadurch ist die Insel Grönland (2,2 Mio. km²) in dieser Kartenprojektion fast so groß dargestellt wie der Kontinent Afrika (30,3 Mio. km²). Die Mercator-Projektion ist also nicht flächentreu. Der Nord- und der Südpol können nicht dargestellt werden, da der projizierte Punkt im Unendlichen liegen würde.

Die Eigenschaft der Winkeltreue ermöglicht es, die auf der Karte abgelesenen Winkel direkt zur Navigation zu nutzen. Bei einer Atlantiküberquerung von z. B. Portugal nach Kuba konnte man im Heimathafen den Kurswinkel zum Zielhafen ermitteln und dann die ganze Fahrt über immer diesen gleichbleibenden Kurs nach dem Kompass steuern. Diese so genannte Loxodrome ist zwar nicht der kürzeste Weg, das wäre die Orthodrome, aber die am einfachsten zu navigierende Strecke, da nicht ständig der Fahrtwinkel angepasst werden muss.

Die Mercator-Projektion ist Gegenstand einer von Arno Peters initiierten Diskussion um ein „eurozentrisches Weltbild“, die er auf die Verwendung dieser Projektion zurückführt. Sein Hauptkritikpunkt ist die mangelnde Flächentreue (auf einer Weltkarte erscheinen polnähere Gebiete wie Europa im Verhältnis größer als äquatornahe Gebiete, die meist in Entwicklungsländern liegen), welche die von ihm entworfene Peters-Projektion bietet. Gegner seiner These entgegnen, dass die Mercator-Projektion zur Vereinfachung der Schiffsnavigation entworfen wurde, nicht um ein bestimmtes Weltbild zu propagieren. Die Verwendung der Mercator-Projektion für eine Weltkarte war zu Mercators Zeit daher auch eher unüblich.

Nutzung

Die Mercator-Abbildung liegt wegen ihrer Winkeltreue fast allen Seekarten und einigen Luftfahrtkarten zugrunde. Die Maßstabsänderungen sind auf größeren Ausschnitten der Erdoberfläche merklich, so dass die am Kartenrand gedruckte Breitengradskala nicht äquidistant ist. Deshalb bekommen Nautiker in ihrer Ausbildung beigebracht, dass die Maßeinheit für Abstandsbestimmungen mit dem Stechzirkel, z. B. 1 Seemeile (Bogenminute auf dem Meridian), immer auf der gleichen Breite wie die eigene Position am linken oder rechten Kartenrand abgegriffen wird.

Normale und transversale Mercatorprojektion

Die transversale Darstellung wird beim UTM-Koordinatensystem angewendet.

Normale Mercator-Projektion

Transversale Mercator-Projektion für 45°E

Transversale Mercator-Projektion für den Nullmeridian

Berechnungsformel

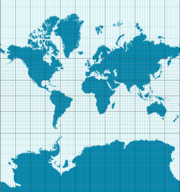
Die folgenden Gleichungssysteme bestimmen die Koordinaten x und y eines Punktes auf einer Mercatorkarte aus seiner geographischen Breite φ und geographischen Länge λ (mit λ₀ als geographischer Länge des Kartenzentrums). Die Erde wird als kugelförmig angenommen; Längen sind mit dem Erdradius dimensionslos gemacht. Die Gleichung für y ist das oben genannte Integral des Kehrwerts des Cosinus der geographischen Breite (anstelle des Tangens bei der Zylinderprojektion):

$\begin{matrix} x &=& \lambda - \lambda_0; \\ \\ y & =& \ln \left[ \tan \left( \frac {1} {4} \pi + \frac {1} {2} \varphi \right) \right] \\ \\ \ & =& \ln \left( \tan \varphi + \sec \varphi \right) \\ \\ \ & =& \frac {1} {2} \ln \left( \frac {1 + \sin \varphi} {1 - \sin \varphi} \right) \\ \\ \ & =& \mathop{\rm artanh} \left(\sin \varphi \right) \\ \\ \ & =& \mathop{\rm arsinh} \left( \tan \varphi \right). \end{matrix}$

Dies ist die Inverse der Gudermannfunktion:

$\begin{matrix} \varphi &=& 2\arctan \left( e^y \right) - \frac{1} {2} \pi \\ \\ \ &=& \arctan \left( \sinh y \right) \\ \\ \ &=& \arcsin \left( \tanh y \right); \\ \\ \lambda &=& x + \lambda_0. \end{matrix}$

Literatur

• Mark Monmonier: Rhumb Lines and Map Wars: A Social History of the Mercator Projection. University of Chicago Press, Chicago 2004, ISBN 0226534316.
• Reinhard Buchholz, Wilhelm Krücken: Die Mercator-Projektion. Zu Ehren von Gerhard Mercator (1512–1594). Becker, Velten 1994 ISBN 3-930640-36-8.
• Rienk Vermij (Hrsg.): Gerhard Mercator und seine Welt. Mercator-Verlag, Duisburg 1997, ISBN 3-87463-254-7.
• Karl Emmerich Krämer: Mercator: eine Biographie. Mercator-Verlag, Duisburg 1980, ISBN 3-87463-088-9.
• Nicholas Crane: Der Weltbeschreiber. G. Mercators Biographie. Droemer-Verlag, 2005, ISBN 3-426-27224-5.
• Nicholas Crane: The Man Who Mapped the Planet. G. Mercators Biographie, engl. Originalfassung. Owl Books, 2004, ISBN 080506625X.
• John Vermeulen: Zwischen Gott und der See: Roman über das Leben und Werk des Gerhard Mercator. Aus dem Niederländischen von Hanni Ehlers. Diogenes, Zürich 2005, ISBN 3-257-06495-0.
• John Vermeulen: Tussen God en de zee: roman over het leven en werk van Gerard Mercator. Niederl. Originalfassung. Kramat, Westerlo 2004, ISBN 90-75212-54-2.

Weblinks

• Ad maiorem Gerardi Mercatoris gloriam Umfangreiche Website von F. Wilhelm Krücken zu Mercator und der mathematischen Entwicklung des nach ihm benannten Kartennetzentwurfs. Dazu eine ausführliche Auseinandersetzung mit der Peters-Projektion.