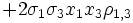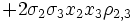Minimum-Varianz-Portfolio

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Die Portfoliotheorie ist ein Teilgebiet der Finanzierung und untersucht das Investitionsverhalten an Kapitalmärkten (z. B. Aktienmarkt). Die Portfoliotheorie geht auf Harry M. Markowitz (Portfolio Selection) zurück und unterstellt bestimmte Annahmen an das Verhalten von Investoren und erzielt so gewisse Aussagen über das Investitionsverhalten.

Zielsetzung

Ziel der Portfoliotheorie ist es, Handlungsanweisungen zur bestmöglichen Kombination von Anlagealternativen zur Bildung eines optimalen Portfolios zu geben. In diesem optimalen Portfolio werden die Präferenzen des Anlegers bezüglich des Risikos und des Ertrags sowie die Liquidität berücksichtigt. Dadurch soll das Risiko eines Wertpapierportfolios, ohne eine Verringerung der zu erwartenden Rendite, minimiert werden. Notwendige Voraussetzung hierbei ist, dass die Wertpapiere nicht vollständig korreliert sind. D.h. wenn ein Korrelationskoeffizient einen Wert von 0 aufweist, besteht keine Möglichkeit das Risiko vollständig zu minimieren, bei einem Korrelationskoeffizienten von +1 müssen Leerverkäufe erlaubt sein um zum Varianzminimum zu gelangen und bei einer Korrelation von -1 kann man das Risiko vollständig eliminieren

Die Portfoliotheorie ist das theoretische Grundgerüst der in der Praxis des Portfoliomanagements verwandten Verfahren.

Annahmen

Die Portfoliotheorie unterstellt einen Investor, der sich in seinem Verhalten ausschließlich an Zahlungsgrößen (Cash flows) orientiert und sein Vermögen mehren will. Er handelt rational und nutzenmaximierend: Das bedeutet, er informiert sich über die Gegebenheiten des Kapitalmarktes und entscheidet sich, indem er Chancen und Risiken gegeneinander abwägt. Dabei scheut er das Risiko (man spricht auch von Risikoaversion). Risikoaverses Verhalten bedeutet, dass ein höheres Risiko nur dann in Kauf genommen wird, wenn der erwartete Ertrag überproportional steigt. Über die Frage, welche Information aus den beobachtbaren Daten des Marktes gewonnen werden kann, hat es in der Finanzierung eine intensive Debatte gegeben (zurückgehend auf die bahnbrechenden Arbeiten von Eugene Fama zur Informationseffizienz).

Um die Analyse zu vereinfachen, nimmt man weiter an, dass der Kapitalmarkt vollkommen ist.

Kern der Portfoliotheorie ist die Unterscheidung in systematisches und unsystematisches Risiko. Dem systematischen Risiko sind alle Wertpapiere am Markt unterworfen, es kann somit nicht wegdiversifiziert werden und ist das Risiko des Anlegens selbst. Das unsystematische Risiko hingegen ist das Risiko, das sich durch Diversifikation, also mit steigender Anzahl an verschiedenen Wertpapieren, verringern lässt. Daher können Anleger für dieses Risiko am Markt keine Prämie erwarten.

Effiziente Portfolios

Ein Portfolio dominiert ein anderes Portfolio, wenn die erwartete Rendite μ größer oder gleich der des anderen Portfolios ist und die Standardabweichung σ ("Wurzel aus Varianz") seines Wertes kleiner oder gleich der des anderen Portfolios ist. Dabei ist ausgeschlossen, dass es sich um dasselbe Portfolio handelt. Die Standardabweichung ergibt sich aus den Kursschwankungen (Streuung) und ist somit das Maß für das Risiko des Portfolios.

Ein Portfolio heißt effizient, wenn es von keinem anderen Portfolio dominiert wird, d. h. wenn kein anderes Portfolio existiert, welches bei gleicher Renditeerwartung ein geringeres Risiko bzw. bei gleichem Risiko eine höhere Rendite hat.

Die Effizienzlinie ist der geometrische Ort aller effizienten Ertrags-Risiko-Kombinationen.

Effiziente Portfolios aus risikolosem und riskanten Wertpapier

Anhand von zwei Wertpapieren lässt sich ein optimaler Risiko-Rendite-Zusammenhang verdeutlichen. In dieser Situation wird, abhängig von der Risikopräferenz des Anlegers, die optimale Strategie ermittelt.

Wir betrachten ein risikoloses (Rendite: r) und ein riskantes Wertpapier (Rendite μ₂). Zusätzlich wollen wir die Möglichkeit von Leerverkäufen (LV) annehmen. In den behandelten Fällen wird ein riskantes Wertpapier, das mit Kurs- und Ausfallrisiko (auch: Währungsrisiko) behaftet ist, betrachtet. Die risikolose Anlage kann durch ein staatliches Wertpapier simuliert werden. Die Laufzeit muss dabei mit der Planungsperiode übereinstimmen. Auf diese Weise lassen sich für das risikolose Instrument Zinsänderungs- und Ausfallrisiken ausschließen.

Es lassen sich vier Fälle unterscheiden:

1. Fall: μ₂ > r ohne Leerverkauf

Die Rendite des riskanten Wertpapiers ist größer als der risikolose Zins und es gibt keine Leerverkäufe. Die einzige Wahl, die der Anleger hat, ist der Anteil $x\in[0,1]$ seiner Mittel, den er in das riskante Papier investiert. Dann fließt der Anteil 1 − x in die risikolose Anleihe.

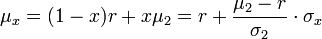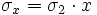Die Effizienzlinie ist eine Gerade aus Ertrags-Risiko-Kombinationen, denn für den Gesamtrendite μ_x gilt $\mu_x = (1-x)r+x\mu_2 = r+\frac{\mu_2-r}{\sigma_2}\cdot\sigma_x$ wobei $\sigma_x=\sigma_2 \cdot x$ mit x aus [0,1]. Dies bedeutet daher:

• Der Rendite-Risiko-Zusammenhang ist linear.
• Der Vorfaktor des Portfoliorisikos entspricht einer normierten Risikoprämie. Dies ist die Überrendite des riskanten Wertpapiers dividiert durch dessen Risiko.

In diesem Fall 1 mit 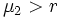$\mu_2>r~$ ohne Leerverkauf sind alle Portfolios auf der durch die Gleichung gegebenen Strecke, d.h. alle Paare (μ_x,σ_x), $x\in[0,1]$, effizient.

Herleitung

Gesucht ist (μ_x,σ_x) in Abhängigkeit vom Mischungsverhältnis (1 − x,x) mit 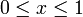$0\le x\le 1$. Allgemein gilt

μ_x = r(1 − x) + μ₂x = r + (μ₂ − r)x

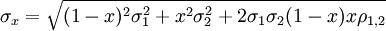$\sigma_x= \sqrt{(1-x)^2 \sigma_1^2+x^2 \sigma_2^2+2 \sigma_1 \sigma_2 (1-x) x \rho_{1,2} }$, wobei ρ₁₂ die Korrelation zwischen den Renditen der betrachteten Papiere ist.

Der hier betrachtete Spezialfall ergibt sich daraus, dass das erste Papier, die Anleihe, risikolos ist, was mathematisch durch σ₁ = 0 ausgedrückt wird, und daraus folgt σ_x = xσ₂.

2. Fall: μ₂ > r mit Leerverkäufen

Die Rendite des riskanten Wertpapiers ist größer als der risikolose Zins und Leerverkäufe sind zulässig. Mathematisch bedeutet die Zulässigkeit von Leerverkäufen, dass der Anteil x der in das riskante Papier inverstierten Mittel nicht mehr durch das Intervall [0,1] eingeschränkt ist. Bei der Zulässigkeit von Leerverkäufen lassen sich die beiden Fälle, in denen das risikolose Wertpapier oder das riskante Wertpapier verkauft wird, unterscheiden.

Leerverkauf der risikolosen Anlage

Der Leverage-Effekt besteht darin, dass bei Leerverkauf des risikolosen Instruments der Erwartungswert des Portfolios steigt, aber auch das Risiko in Form größerer Streuung. Leerverkauf der risikolosen Anleihe bedeutet x > 1, das heißt man investiert mehr Mittel in das riskante Papier. Für die Gesamtrendite μ_x ergibt sich 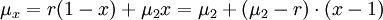$\mu_x=r (1-x) + \mu_2 x=\mu_2+(\mu_2-r) \cdot (x-1)$ mit x > 1.

Leerverkauf der riskanten Anlage

Der Leerverkauf des rsikanten Papiers bedeutet x < 0. Die Gesamtrendite 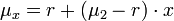$\mu_x=r+(\mu_2-r)\cdot x$ ist damit kleiner als die geforderte Mindestrendite r.

Der formale Ablauf besteht im Ausleihen einer Aktie, deren anschließenden Verkauf und Investition der so erhaltenen Mittel in das risikolose Papier. Die Ausleihe bedeutet, dass der Partei, die die Aktie zur Ausleihe bereitstellt, alle aus dem Besitz der Aktie resultierenden Zahlungen (Dividenden) erstattet werden, und dass die Aktie am Ende der Laufzeit am Markt zurückgekauft und dieser Partei zurückgegeben wird.

Der Leerverkäufer trägt dasselbe Risiko wie ein Aktienhalter und erwirtschaftet im hier vorliegenden Fall μ₂ > r eine geringere Rendite, als man auch risikolos erhalten könnte. Deshalb sind durch Leerverkauf der riskanten Anlage erzeugte Portfolios in diesem Fall nicht effizient.

3. Fall μ₂ < r ohne Leerverkauf

Die Rendite des riskanten Wertpapiers ist kleiner als der risikolose Zins und es gibt keine Leerverkäufe. Für die Gesamtrendite gilt $\mu_x = r - (r-\mu_2)\cdot x,\, x\in[0,1]$.

In diesem Fall ist ein Portfolio, das nur in das risikolose Instrument investiert, effizient, denn durch das Eingehen eines erhöhten Risikos, das heißt durch eine Wahl x > 0, vermindert man die Rendite.

4. Fall μ₂ < r mit Leerverkäufen

Leerverkäufe sind zulässig: Durch einen Leerverkauf des riskanten Instruments, das heißt durch eine Wahl x < 0, lässt sich die Portfoliorendite 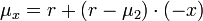$\mu_x = r + (r-\mu_2)\cdot (-x)$ beliebig steigern, natürlich nur bei gleichzeitiger, durch den Leerverkauf bedingten Erhöhung des Gesamtrisikos.

Effiziente Portfolios aus zwei riskanten Wertpapieren

Es lassen sich folgende Fälle unterscheiden:

• Die Rendite des zweiten Wertpapiers ist größer als die des ersten und die Varianz des zweiten Wertpapiers ist größer als die des ersten.

Die Aufhebung der Leerverkaufsbeschränkung führt nicht zu Änderungen im Minimum-Varianz-Portfolio wenn die Korrelation ρ bestimmte Werte annimmt, die sich aus dem Verhältnis der Standardabweichungen beider Titel ergibt. Dies bedeutet dass beide Wertpapiere im Ausgangsportfolio mit positiven Anteilen vertreten sind.

Iso-Ertragslinien

Ein optimales Portfolio nach diesem Kriterium liegt bei (x₁,x₂) = (0,1)

Budgetgerade

Iso-Ertragslinie μ₁

Iso-Ertragslinie μ₂

Iso-Risikolinien

Ein optimales Portfolio nach diesem Kriterium liegt nicht an den Extrempunkten.

Budgetgerade ohne Leerverkaufsmöglichkeit

Iso-Ertragslinie μ₁

Iso-Ertragslinie μ₂

• Die Rendite des zweiten Wertpapiers ist größer als die des ersten und die Varianz des zweiten Wertpapiers ist kleiner oder gleich der ersten.

Analytische Bestimmung des global varianzminimalen Portfolios

unkorrelierte Wertpapiere

Bei unkorrelierten Wertpapieren tritt immer ein Diversifikationseffekt auf.

$x_1^*=\frac{\sigma_2^2}{\sigma_1^2+\sigma_2^2}$

$x_2^*=\frac{\sigma_1^2}{\sigma_1^2+\sigma_2^2}$

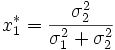
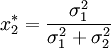
korrelierte Wertpapiere

2 riskante Wertpapiere (ohne LV)

Risikodiversifikation in Abhängigkeit vom Korrelationskoeffizienten ρ:

Form eines Hyperbelastes

Die Wahl des Portfolios ergibt das Minimum-Varianz-Portfolio:

$x_1^*=\frac{\sigma_2^2-\sigma_1\cdot\sigma_2\cdot\rho}{\sigma_1^2+\sigma_2^2-2\cdot\sigma_1\cdot\sigma_2\cdot\rho}$

$x_2^*=\frac{\sigma_1^2-\sigma_1\cdot\sigma_2\cdot\rho}{\sigma_1^2+\sigma_2^2-2\cdot\sigma_1\cdot\sigma_2\cdot\rho}$

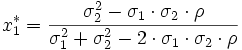
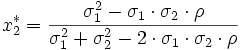
Ist die Kovarianz bekannt so sieht die Formel im ersten Fall wie folgt aus: $x_1^*=\frac{\sigma_2^2-\sigma_{12}}{\sigma_1^2+\sigma_2^2-2\sigma_{12}}$

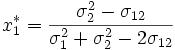
Zu beachten

• Wenn zwei Wertpapiere zur Auswahl stehen, heißt das nicht, dass eins von beiden effizient sein muss. Gegenbeispiel: ρ < 1 für 2 Wertpapiere mit μ₁ = μ₂ und σ₁ = σ₂ gilt σ_MVP < σ_i. MVP bezeichnet das Minimum-Varianz-Portfolio.

Effiziente Portfolios aus drei riskanten Wertpapieren

2 Fälle

• Global varianzminimales Portfolio mit negativen Anteilen:

Dies lässt sich in einem x₁-x₂-Diagramm, welches die Aufteilung auf Wertpapier 1 und 2 (und damit implizit auf Wertpapier 3) sowie in einem μ-σ-Diagramm, welches die Effizienzlinie zeigt, darstellen.

x₁-x₂-Diagramm: x₃ ergibt sich aus dem Rest zwischen x₁ und x₂. Die Ordinate ist dann der Ort aller Mischungen aus Wertpapier 1 und 3 und die Abzisse die Mischung aus den Wertpapieren 2 und 3.

• Global varianzminimales Portfolio mit positiven Anteilen:

Dies lässt sich in einem x₁-x₂-Diagramm, welches die Aufteilung auf Wertpapier 1 und 2 (und damit implizit auf Wertpapier 3) sowie in einem μ-σ-Diagramm, welches die Effizienzlinie zeigt darstellen

Herleitung

Aus x₁ + x₂ + x₃ = 1 ergeben sich zwei abhängige Variable.

μ_x = μ₁x₁ + μ₂x₂ + (1 − x₁ − x₂)μ₃

$\sigma_x^2$= $x_1^2 \sigma^2_1+x_2^2 \sigma^2_2+ (1-x_1-x_2)^2 \sigma^2_3$$+2 \sigma_1 \sigma_2 x_1 x_2 \rho_{1,2}~$

$+2 \sigma_1 \sigma_3 x_1 x_3 \rho_{1,3}~$ $+2 \sigma_2 \sigma_3 x_2 x_3 \rho_{2,3}~$

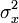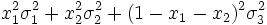
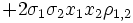
Effiziente Portfolios für n Wertpapiere

Dies lässt sich nur noch rechnerisch bestimmen mit $\min_{x1...xn}\Sigma [\rho_{ij}\cdot\sigma_i\cdot\sigma_jx_ix_j]$

Es müssen dabei die Restriktionen:

• Mindestrendite
• Budgetbedingung
• eventuell auch Leerverkaufsbeschränkung berücksichtigt werden.

Mischung effizienter Portfolios

Bei Dachfonds stellt sich bspw. die Frage ob eine Mischung von effizienten Portfolios wieder ein effizientes Portfolio ergibt. Dies muss nicht zutreffen, da

• im Falle, dass Leerverkäufe nicht zulässig sind, die Effizienzlinie geknickt ist. Bildet man nun ein Portfolio aus zwei Wertpapieren auf einem unterschiedlichen Teil der Linie, liegt dieses Portfolio nicht mehr auf der Effizienzlinie.
• im Fall, dass Leerverkäufe zulässig sind, ein Leerverkauf eines effizienten Portfolios ineffiziente Portfolios erzeugen kann.

Optimales Portfolio

Man versucht, ein optimales Portfolio zu finden. Dies ist abhängig von der Risikopräferenz des Investors. Bei optimalen Portfolios gilt, dass die Steigung der Indifferenzkurve des Investors gleich der Steigung der Effizienzlinie ist.

Die komparative Statik ergibt, dass der Anteil des riskanten Wertpapiers:

• stets größer Null ist
• wächst mit der Überschussrendite
• fällt mit steigendem Risiko des riskanten Wertpapiers
• fällt mit steigender Risikoaversion des Investors

Die Investoren, die sich an der erwarteten Rendite und dem erwartetem Risiko orientieren, halten nie ein vollständig risikoloses Portfolio. Dies liegt daran, dass die Investoren im μ-σ-Diagramm eine waagerechte Tangente der Indifferenzkurve im Punkt σ = 0 besitzen.

Ergebnisse

Das wichtigste Ergebnis der Portfoliotheorie ist die Risikodiversifikation: es existiert für jeden Investor ein so genanntes optimales Portfolio aus allen Anlagemöglichkeiten, das dessen Risiko-Chancen-Profil bestmöglich abbildet. Dieses optimale Portfolio hängt dabei weder von dem ursprünglichen Vermögen des Investors noch seiner unmittelbaren Risikoeinstellung ab. Vielmehr spielen nur die Risiko-Rendite-Kombinationen der gehandelten Titel eine Rolle. Der Beweis der Aussage geht auf James Tobin zurück, nach ihm wird dieses Theorem auch Tobin-Separation genannt.

Kritik

• Sowohl die Annahmen als auch die Aussagen werden von der ökonomischen Wissenschaft durchaus kritisch bewertet, dennoch gilt die Portfoliotheorie als gesichert.
• Prognosen sind ungenau, da sie sich nur auf historische Daten beziehen.
• Die Anlegerpräferenzen sind nicht eindeutig operationalisierbar.
• In der Realität sind Renditen nicht normalverteilt.
• Es besteht ein enormer Aufwand der Datenerhebung. Bei 100 Wertpapieren sind mehr als 5000 Werte zu erheben und 100 Gleichungen zu lösen.
• Realistischere, dynamische Modelle sind nicht überschaubar.
• Auswirkungen, die eine Investition auf den Kurs haben könnte, werden nicht berücksichtigt.
• Eine Grundannahme der Portfoliotheorie ist u.a. dass man aus der Vergangenheit keine verlässlichen Schlüsse auf die Zukunft ziehen und diese generell nicht vorhersehen kann. Dennoch besteht ein wesentlicher Faktor der Portfoliotheorie auf Schätzungen etwa der zukünftigen Renditen, die aber niemand verlässlich vorhersagen kann. Schätzfehler bei der Bewertung der zukünftigen Renditen haben enorme Auswirkungen auf die Mean-Variance-Optimierung und die Asset Allocation. ^[1]
• Die zu Grunde liegende Theorie der effizienten Märkte scheint durch die Erfolge z. B. eines Warren Buffett in der Praxis widerlegt. Dieser begründet ja seinen Erfolg auf unterbewertete Unternehmen, die es in einem effizienten Markt per Definition nicht gibt. Allerdings sind auch langfristige Anlageerfolge wie der Warren Buffetts statistisch möglich, ohne die Theorie effizienter Märkte zu widerlegen.

Siehe auch

• Capital Asset Pricing Model
• Home Bias

Weblinks

• Grundzüge der Portfoliotheorie bei DeiFin.de
• Hier wird die Portfoliotheorie diadaktisch gut aufbereitet erklärt

Quellenangaben

1. ↑ Vgl. Chopra/Ziemba (1993)

Literatur

• Edwin J. Elton, Martin J. Gruber, Stephen J. Brown, William N. Goetzman: Modern Portfolio Theory and Investment Analysis. 6. ed., John Wiley & Sons, ISBN 0-471-23854-6
• Stephen A. Ross, Randolph W. Westerfield, Jeffrey Jaffe: Corporate Finance. 7. ed., McGraw-Hill Irwin, Boston 2005, ISBN 0-07-282920-6
• Harry M. Markowitz: Portfolio Selection, Journal of Finance 7(1952), S. 77-91. ISSN 0022-1082
• Detlef Mertens: Portfolio-Optimierung nach Markowitz; ISBN 3-937519-09-2
• Kurt M. Maier: Risikomanagement im Immobilien- und Finanzwesen; ISBN 3-8314-0756-8
• Klaus Spremann: Portfoliomanagement; ISBN 3-486-57939-8
• Hagenloch, T.: Value Based Management und Discounted Cash Flow-Ansätze. Eine verfahrens-und aufgabenorientierte Einführung ISBN 3-8334-8376-8