Capital Asset Pricing Model

Das Capital-Asset-Pricing-Model (CAPM) (zu deutsch: Preismodell für Kapitalgüter bzw. Kapitalgutpreismodell) ist ein Kapitalmarktgleichgewichtsmodell, das die Portfoliotheorie um die Frage erweitert, welcher Teil des Gesamtrisikos eines Investitionsobjekts nicht durch Risikostreuung (Diversifikation) zu beseitigen ist und erklärt, wie risikobehaftete Anlagemöglichkeiten im Kapitalmarkt bewertet werden. Der Kern des CAPM, das Modell der Wertpapierlinie, beschreibt eine lineare Abhängigkeit der zu erwartenden Rendite einer Kapitalanlage von nur einer Risikoeinflussgröße (Ein-Faktor-Modell). Ziel des CAPM ist es letztlich, Gleichgewichtskurse für einzelne riskante Anlagemöglichkeiten (im Folgenden: Wertpapiere) im Portfoliozusammenhang unter Unsicherheit (Risiko) herzuleiten.

Geschichte

Das CAPM wurde von William F. Sharpe, John Lintner und Jan Mossin in den sechziger Jahren unabhängig voneinander entwickelt und baut auf der Portfoliotheorie von Harry Markowitz auf.

Problemstellung

Gegenstand der Portfoliotheorie ist die Investitionsentscheidung eines (zumeist) risikoaversen Anlegers bei Auswahl aus risikobehafteten und risikolosen Wertpapieren. Unter der Normalverteilungsannahme für Wertpapierrenditen ist diese Entscheidung alleine von der erwarteten Rendite und dem Risiko der Wertpapiere abhängig. Dabei wird die erwartete Rendite aus dem Mittelwert, das Risiko aus der Standardabweichung vergangener Kursdaten abgeleitet. Grundgedanke der Portfoliotheorie nach Markowitz ist die Möglichkeit der Diversifikation durch Bildung von Wertpapierportfolien.

Das CAPM geht einen Schritt weiter und bestimmt theoretische Gleichgewichtskurse, die sich einstellen, wenn risikoaverse Marktteilnehmer entsprechend der Portfoliotheorie effiziente Portfolios zusammenstellen.

Die Preisbildung eines Wertpapiers hat Auswirkungen auf die Preisbildung der anderen Wertpapiere. Die Gleichgewichtspreise müssen daher simultan bestimmt werden.

Gleichgewichtspreise sind wichtig für aggregierte Risikozuschläge oder Risikoabschläge:

• Bei der Unternehmensbewertung dienen sie zur Bestimmung der Kapitalkosten (WACC).
• Mit den Gleichgewichtspreisen lässt sich die Performance von Aktienfonds beurteilen. Damit lässt sich eine Aussage treffen, ob das zusätzliche Risiko angemessen ist bezogen auf die durchschnittliche zusätzliche Rendite.

Aufbau des Modells

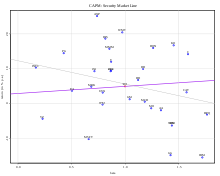SML (violett) des CAPM. Markt ist hier der Dow Jones Industrial Average Index, geschätzt wurden zwischen Jan 2004 und Nov 2006 monatliche Daten, der Zinssatz wurde als konstant 2,9 % angenommen. Die Regressionsgerade ist grau eingezeichnet.

Die Vorstufe des CAPM ist das Modell der Kapitalmarktlinie (KML, engl. Capital Market Line, CML), wohingegen das Modell der Wertpapiermarktlinie (WML, engl. Security Market Line, SML) das eigentliche Kernmodell bildet. Das CAPM baut auf den gleichen Voraussetzungen auf wie die Portfoliotheorie. Hinzu kommen noch die stark vereinfachenden Annahmen des vollkommenen Kapitalmarkts, Risikoaversion und homogene Erwartungen der Anleger sowie normalverteilte Wertpapierrenditen.

Aus diesen Annahmen folgt, dass im Marktgleichgewicht sämtliche Anleger ein in gleicher Weise zusammengesetztes Portfolio halten, sofern risikobehaftete Wertpapiere und eine risikolose Anlage (der Kapitalmarkt) zur Verfügung stehen. Genauer gesagt hält jeder Anleger eine Mischung aus dem Marktportfolio M und der risikolosen Anlage. In diesem sog. Marktportfolio sind alle gehandelten risikobehaftenen Wertpapiere im Verhältnis ihrer Marktwerte vorhanden. Die Annahme des Gleichgewichtszustands bedeutet: Wenn es nicht-μ-σ-effiziente Wertpapiere geben würde, dann würden sie verkauft und gegen μ-σ-effiziente Wertpapiere eingetauscht werden. Der Verkauf solcher Wertpapiere drückt deren Preis (falls die Competitivity-Bedingung nicht angenommen wird), lässt also die Rendite des betroffenen Wertpapiers steigen. Im Gleichgewichtszustand sind alle solchen Transaktionen bereits abgeschlossen, was bedeutet, dass es keine Wertpapiere mehr auf dem betrachteten Kapitalmarkt gibt, die nicht μ-σ-effizient sind. Daher besteht das Marktportfolio nur noch aus μ-σ-effizienten Wertpapieren und muss daher selbst effizient sein.

Sind die erwarteten Renditen und die Risiken der einzelnen Wertpapiere bekannt, lässt sich auch die erwartete Rendite und das Risiko des Marktportfolios berechnen. Die erwartete Rendite des Marktportfolios wird in der Kapitalmarkttheorie als „Kapitalkosten unter Risiko“ oder auch „risikoadjustierte Kapitalkosten“ bezeichnet.

Durch die Möglichkeit, unbegrenzt risikolos Geld anzulegen oder aufzunehmen, kann der Anleger in einem nächsten Schritt je nach Grad seiner Risikoaversion die gewünschte Risikoposition durch Mischung der risikolosen Anlagemöglichkeit mit einer Anlage in das risikoeffiziente Marktportfolio (bzw. bei geringerer Risikoaversion durch Kreditaufnahme und Anlage in das Marktportfolio) erzeugen. Diese Aufteilung des anzulegenden Kapitals in ein stets identisch strukturiertes Marktportfolio unabhängig von der persönlichen Risikoneigung wird als Tobin-Separation oder “Two Fund Separation” bezeichnet.

Modell der Kapitalmarktlinie (Capital Market Line)

Um in dieser Modellwelt die erwartete Rendite bzw. den Kurs eines einzelnen Wertpapiers im Portfoliozusammenhang auf mathematisch-statistischem Wege herzuleiten, werden folgende Festlegungen getroffen:

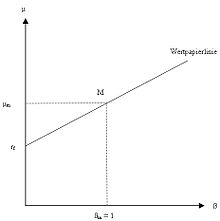
Der Unterschied zwischen der erwarteten Rendite des Marktportfolios M („Kapitalkosten unter Ungewissheit“) und dem sicheren Zinssatz wird Marktpreis für das Risiko genannt. Die Risikomenge eines jeden Wertpapiers in einem wohl diversifizierten Portfolio wird Beta (β) genannt. Das Risiko des Marktportfolios M selbst beträgt 1. Der β-Faktor eines individuellen Wertpapiers ist definiert als der Quotient aus der statistischen Kovarianz des betreffenden Wertpapiers zum Marktportfolio M und der Varianz des Marktportfolios. Der Beta-Faktor bezieht sich ausschließlich auf das nicht weiter reduzierbare Risiko im Portfoliozusammenhang (das so genannte „systematische Risiko“) und stellt somit den maßgeblichen Beitrag zum Risiko eines jeden Portfolios dar.

Nach einer sich anschließenden mathematischen Optimumsbestimmung ergibt sich nun die zentrale Aussage des CAPM:

$\mu_i=r_f+(\mu_m-r_f)\cdot\beta_i$ mit $\beta_i=\frac{Cov(r_M;r_i)}{\sigma_M^2}$

Der Beta-Wert für die sichere Anlage ist $\beta_{r_f}=\frac{Cov(r_f;r_m)}{\sigma_M^2}=0.$
Der Beta-Wert für das Marktportfolio beträgt $\beta_M=\frac{COV(r_M;r_M)}{\sigma_M^2}=\frac{Var(r_M)}{\sigma_M^2}=1.$

Formel zur Berechnung des risikolosen Zinssatzes aus den anderen (bekannten) Parametern:

$r= \frac{\beta_i \mu_M-\mu_i}{\beta_i-1}$

Wertpapierlinie (Security Market Line)

Die erwartete Rendite μ_i eines risikobehafteten Wertpapiers (zum Beispiel Aktie) setzt sich im Marktgleichgewicht zusammen aus dem risikolosen Zinssatz r_f und einer Risikoprämie. Die Risikoprämie ist das Produkt aus dem Marktpreis für das Risiko (μ_m − r_f) und der Risikomenge β_i der betrachteten Anlagemöglichkeit.

Dabei gilt: Je höher der Beta-Faktor eines Wertpapiers, desto höher fällt seine erwartete Rendite aus und umgekehrt. Mit anderen Worten: Investoren sind nur dann bereit, ein Wertpapier mit einem hohen Risiko (β) zu halten, wenn eine entsprechend hohe Rendite zu erwarten ist.

Unter den gesetzten Annahmen einperiodiger Planung lässt sich für jedes Wertpapier die so ermittelte Rendite auf einfache Weise in einen Gleichgewichtskurs überführen. Der Gleichgewichtskurs dient als Maßstab dafür, ob ein einzelnes Wertpapier(portfolio) im Einklang mit seinem Risiko durch den Markt bewertet wird.

Anwendungen

• Aktienbewertung
• Performanceanalyse
• Bewertung von Investitionsprojekten, Unternehmensbewertung
• Portfoliomanagement
• Marktwertmaximierende Investitionsentscheidung

Kritische Würdigung des CAPM

Die strengen Prämissen des CAPM mögen auf den ersten Blick unrealistisch erscheinen. Jedoch konnte in zahlreichen, sich einander widersprechenden Studien das Modell empirisch nicht eindeutig falsifiziert werden. Offensichtlich ist jedoch, dass sich am Kapitalmarkt Effekte beobachten lassen, die im Widerspruch zum CAPM stehen. Dazu gehören je nach empirischer Untersuchung der Januareffekt oder der Kleinfirmeneffekt. Allerdings hat bereits Sharpe im Jahr 1964 geäußert, dass eine Theorie nicht in der Realitätsnähe ihrer Prämissen überprüft werden sollte, sondern in der Annehmbarkeit ihrer Implikationen. So liefert das CAPM nicht nur die bekannteste Erklärung für die Austauschbeziehung (Trade-off) zwischen Rendite und Risiko, sondern ist z.B. ein wichtiges Instrument bei der Performancemessung von Investmentfonds. In den 1970er und 80er Jahren wurden des Weiteren einige der ursprünglichen Modellannahmen durch realistischere ersetzt und das Modell auf dieser Basis neu aufgestellt. Es zeigte sich, dass auch unter weniger strengen Annahmen die Kernaussage des Modells der Wertpapierlinie weiterhin Bestand hat.

Dies überrascht nicht, da die aus Modellen abgeleiteten Aussagen zwangsläufig logisch wahr sein müssen, sofern kein logischer Denkfehler innerhalb des Modells vorliegt. Einer empirischen Überprüfung entzieht sich das CAPM deshalb, weil sich das Markt-Portfolio aller risikobehafteten Vermögenswerte nicht rekonstruieren lässt (Kritik von Roll). Aufgrund dessen greift man auf Teil-Portfolios zurück. Tests dieser Teil-Portfolios geben aber nur Aufschluss über die Risikoeffizienz dieser Teil-Portfolios; ein Rückschluss auf das Markt-Portfolio ist nicht möglich. Eine empirische Überprüfung der Risikoeffizienz des Markt-PFs ist gemäß Richard Roll somit nicht möglich. Überdies kann das CAPM dem Anspruch, die Börsenkurse in der Realität zu erklären, nicht gerecht werden, da sich für reale Kapitalmärkte kaum ein Gleichgewichtszustand postulieren lässt.

Problematisch für die empirische Überprüfung des CAPM ist des Weiteren, dass es sich bei dem CAPM um ein ex-ante-Modell handelt. Tests auf die Risikoeffizienz des Markt-PFs werden allerdings mit ex-post-Daten durchgeführt. Weitere Probleme bei der empirischen Überprüfung sind der Selection Bias sowie Strukturbrüche des Portfolios.

Weiterhin wird für das CAPM implizit eine gaußsche Normalverteilung der Renditen unterstellt. An den Kapitalmärkten konnten jedoch in jüngerer Zeit Renditeschwankungen mit Streuung mit einem Vielfachen der Streuung ("fat tails") beobachtet werden. Diese Beobachtung der Renditeverteilung steht jedoch in einem klaren Widerspruch zu den Annahmen des CAPM.

Weblinks

• Das CAPM

Literatur

• William Sharpe, Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk, 1964, in: Journal of Finance, Seiten 425-442
• Arnold, Glen, Corporate Financial Management, 3. Auflage, Harlow u.a.2005, S. 276-358 und S. 872 -905.
• Brealey/Myers, Principles of Corporate Finance, New York 1996, S. 143-190.