Mischverteilung

Der Begriff Mischverteilung oder zusammengesetzte Verteilung stammt aus der Wahrscheinlichkeitsrechnung.

Es wird zur Einführung ein Merkmal X betrachtet, das zwei Grundgesamtheiten G₁ und G₂ entstammt. Im stochastischen Modell handelt es sich also eigentlich um zwei Zufallsvariablen X₁ und X₂, idealerweise vom gleichen Verteilungstyp. Die Anteile der beiden Merkmale sind a₁ und a₂. Beobachtet wird die Verteilung von X, die bestimmt wird von der totalen Wahrscheinlichkeit

$P(X \le x) = P(X \le x|X \mbox{ aus } G_1) \cdot a_1 + P(X \le x|X \mbox{ aus } G_2) \cdot a_2$

bzw. als Mischverteilung mit den entsprechenden Verteilungen

$P(X \le x) = F_1(x) \cdot a_1 + F_2(x) \cdot a_2$.

Definition

Lässt sich die Dichtefunktion einer stetigen Zufallsvariablen X als

$f(x) = \sum_{k=1}^K a_k f_k ( x)$

schreiben, so sagt man, dass X einer Mischverteilung folgt. Dabei sind die f_k(x) Dichtefunktionen von stetigen Zufallsvariablen X_k und die a_k Wahrscheinlichkeiten mit

$\sum_{k=1}^{K} a_k = 1$.

Man kann leicht zeigen, dass unter diesen Bedingungen auch

$\int_{-\infty}^{\infty} f(x) dx = 1$

gilt.

Entsprechend ergibt sich die Wahrscheinlichkeitsfunktion der diskreten Mischverteilung als

$f(x_i) = \sum_{k=1}^K a_k f_k (x_i)$

Eigenschaften

Für die Momente von X gilt:

$E(X^p) = \sum_{k=1}^K a_k \, E(X_k^p),~p \in \{1,2,3,...\}.$

Dies folgt (im stetigen Fall) aus

$E(X^p) = \int_{-\infty}^{\infty} x^p f(x) dx = \int_{-\infty}^{\infty} x^p \left( \sum_{k=1}^K a_k f_k (x) \right) dx = \sum_{k=1}^K a_k \left( \int_{-\infty}^{\infty} x^p f_k(x) dx \right).$

Eine analoge Rechnung ergibt die Formel für den diskreten Fall.

Beispiel

Verteilung des Gewichts der Forellen (g)

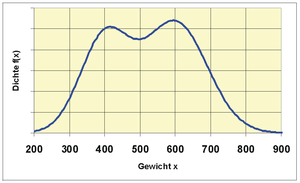
Ein Forellenzüchter verkauft Forellen in großen Mengen. Es wird im Herbst beim Leeren der Teiche eine Bestandsaufnahme gemacht. Dabei werden die herausgefischten Forellen gewogen. Es ergibt sich die Verteilung des Gewichts, wie in der Grafik zu ersehen ist. Die Zweigipfligkeit der Verteilung deutet auf eine Mischverteilung hin. Es stellt sich heraus, dass die Forellen zwei verschiedenen Teichen entstammen. Die Forellengewichte aus dem ersten Teich sind normalverteilt mit dem Erwartungswert 400 g und der Varianz 4900 g² und die aus dem zweiten Teich mit dem Erwartungswert 600 g und der Varianz 8100 g². Aus dem ersten Teich stammen 40% der Forellen, aus dem zweiten 60%.

Siehe auch

Bayessches Theorem, Diskriminanzanalyse, Kontaminierte Normalverteilung