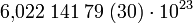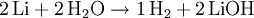- Mol (Einheit)
-
Einheit Norm SI-Einheitensystem Einheitenname Mol Einheitenzeichen mol Beschriebene Größe(n) Stoffmenge Größensymbol(e) n Dimensionssymbol N In SI-Einheiten SI-Basiseinheit Benannt nach Molekül Das Mol (Einheitenzeichen: mol) ist die SI-Basiseinheit der Stoffmenge. Wichtig ist das Mol für Mengenangaben bei chemischen Reaktionen.
Der Begriff „Mol“ wurde 1893 von Wilhelm Ostwald geprägt und ist vermutlich von „Molekül“ abgeleitet. Ältere Bezeichnungen sind Grammatom (nur für Elemente) und Grammmolekül (nur für Verbindungen).
Inhaltsverzeichnis
Definition
Im SI-Einheitensystem ist das Mol eine Basiseinheit und so definiert:
- Das Mol ist die Stoffmenge eines Systems, das aus ebenso viel Einzelteilchen besteht, wie Atome in 12 Gramm des Nuklids Kohlenstoff-12 (12C) enthalten sind; sein Symbol ist „mol“.
- Wenn das Mol benutzt wird, müssen die verwendeten Einzelteilchen angegeben werden; es kann sich dabei um Atome, Moleküle, Ionen, Elektronen, sonstige Teilchen oder spezifizierte Gruppen solcher Teilchen handeln.[1]
Anders ausgedrückt haben 12 Gramm Kohlenstoff-12 genau 1 Mol Atome. 1 Mol natürlicher Kohlenstoff hingegen hat aufgrund des Isotopengemischs eine Masse von 12,0107 Gramm. Teilchenzahl und Stoffmenge sind einander proportional, sodass eine beliebige dieser beiden Größen als Maß für die andere dienen kann.
Die Teilchenzahl pro 1 Mol Stoffmenge (Avogadro-Konstante) beträgt:
Ein Mol eines Stoffes enthält also ca. 602 Trilliarden Teilchen dieses Stoffes.
Folgende Zahlenwerte sind identisch:
- Der Zahlenwert der Masse eines Teilchens in der atomaren Masseneinheit u (welcher in der Chemie früher als „relative Atommasse“ oder „Atomgewicht“ bezeichnet wurde).
- Der Zahlenwert der Masse von einem Mol dieses Teilchens in Gramm (Beispiel unten: Molare Masse).
Historisches
Im SI ist 1971 das Mol als Basiseinheit eingeführt worden. Damit wurde der Anwendungsbereich des SI auf die Chemie ausgedehnt. Vor Etablierung des SI ist das Mol überwiegend als Masseneinheit angesehen worden. So heißt es in DIN 1310 „Gehalt von Lösungen“ vom April 1927: „Als Masseneinheiten dienen ... das Mol, d. h. soviel Gramm des Stoffes, wie sein Molekulargewicht angibt...“. Allerdings wurde durch die Anwendung des Molekular„gewichts“ hier eine Stoffmasse - keine -menge heutiger Sicht - beschrieben und als „Stoffmenge“ bezeichnet. In der heutigen Mol-Definition des SI hingegen wird die Stoffmenge von Teilchenzahl und Masse formal klar unterschieden.
Molares Volumen
Das molare Volumen eines Stoffes ist eine stoffspezifische Eigenschaft, die angibt, welches Volumen ein Mol eines Stoffes ausfüllt. Für ideale Gase gilt, dass ein Mol bei Normalbedingungen (273,15 K, 101325 Pa) ein Volumen von 22,414 Litern einnimmt. Für reale Gase, Feststoffe und Flüssigkeiten ist das molare Volumen hingegen stoffabhängig.
Molare Masse
Die molare Masse M ist der Quotient aus Masse und Stoffmenge eines Stoffes. In der Einheit g/mol besitzt sie denselben Zahlenwert wie die Atommasse, also die Masse eines Atomes, in u (atomare Masseneinheit). Ihre Bedeutung ist äquivalent zum früheren „Atomgewicht“ in der Chemie.
Berechnung von Stoffmengen
Zur Berechnung wird folgende Formel verwendet:
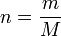
Dabei bezeichnet n die Stoffmenge, m die Masse und M die molare Masse. M kann für chemische Elemente Tabellenwerken entnommen und für chemische Verbindungen bekannter Zusammensetzung aus solchen Werten errechnet werden.
Die atomare Masse, die für jedes chemische Element in Tabellen angegeben wird, bezieht sich dabei auf das natürliche Isotopengemisch. So ist zum Beispiel als Atommasse für Kohlenstoff 12,0107 u angegeben. Dieser Wert ist zum Beispiel für in 13C angereichertes Material nicht anzuwenden. Während bei stabilen Elementen die Abweichungen von Isotopenmischungen, wie sie in der Natur vorkommen, relativ gering sind, kann insbesondere bei radioaktiven Elementen das Isotopengemisch stark von der Herkunft und dem Alter des Materials abhängen.
Verwendung der Einheit Mol bei Konzentrationsangaben
Die Einheit Mol findet häufig Verwendung in zusammengesetzten Einheiten zur Angabe von Konzentrationen (Lösungen, Säuregehalt von Lösungen usw.). Eine der häufigsten Verwendungen ist die x-molare Lösung (das x steht darin für eine beliebige rationale positive Zahl). Die Bedeutung ist
- Beispiel:
- Eine 2,5-molare A-Lösung enthält 2,5 Mol des gelösten Stoffes A in 1 Liter der Lösung.
- Siehe hierzu auch: Molarität
Beispiele
Masse von 1 Mol Helium
- 1 Atom Helium wiegt ungefähr 4 u (ein Helium-Atom hat 2 Protonen und 2 Neutronen, die Elektronen sind in diesem Beispiel wegen ihrer sehr geringen Masse vernachlässigt. Helium-Gas ist einatomar, daher bezieht sich im folgenden Beispiel das Mol auf He-Atome, ohne dass das einer besonderen Erwähnung bedarf.)
- 1 mol Helium wiegt also etwa 4 g und enthält ungefähr 6,022·1023 Helium-Atome (Avogadro'sche Zahl).
Masse von 1 Mol Wasser
- 1 mol eines Stoffes enthält ungefähr 6,022·1023 Teilchen.
- Das Volumen von 1 mol eines idealen Gases unter Normalbedingungen beträgt etwa 22,4 Liter.
- 1 Wassermolekül H2O besteht aus 1 Sauerstoffatom + 2 Wasserstoffatomen.
- Das Sauerstoffatom besitzt 16 Nukleonen (Kernteilchen, also Neutronen und Protonen), Wasserstoff 1 Kernteilchen (ein Proton)
- Ein Wassermolekül enthält demnach 18 Nukleonen.
- Die Masse eines Kernteilchens ist ungefähr 1,6605·10-24 g.
- 1 Wassermolekül hat somit die Masse 18 · 1,6605·10-24 g
- Die Masse von 1 mol Wasser ist das 6,022·1023-fache der Masse eines Wassermoleküls
- Die Masse von 1 mol Wasser ist somit 6,022·1023 · 18 · 1,6605·10-24 g = 18 g
Herstellung von Lithiumhydroxid aus Lithium und Wasser
Bei der Bildung von LiOH werden also pro zwei Lithiumatomen zwei Wassermoleküle verbraucht. Weil in jedem Mol von jeder Substanz gleich viele Teilchen vorhanden sind (siehe oben), braucht man 2 mol Lithium und 2 mol Wasser oder eine beliebige andere Stoffmenge im 2:2-Verhältnis.
- 2-mal 6,94 g Lithium und 2-mal 18 g Wasser reagieren also zu 1-mal 2 g Wasserstoff und 2-mal 23,94 g Lithiumhydroxid
Präfixe
SI-Präfixe Name Yotta Zetta Exa Peta Tera Giga Mega Kilo Hekto Deka Symbol Y Z E P T G M k h da Faktor 1024 1021 1018 1015 1012 109 106 103 102 101 Name Yokto Zepto Atto Femto Piko Nano Mikro Milli Zenti Dezi Symbol y z a f p n µ m c d Faktor 10−24 10−21 10−18 10−15 10−12 10−9 10−6 10−3 10−2 10−1 Literatur
- ↑ Übersetzt aus http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf
- ↑ CODATA (2006): Avogadro constant, NIST.
Siehe auch
Wikimedia Foundation.