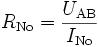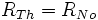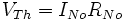Norton-Äquivalent

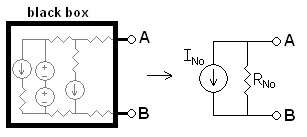
In der Theorie linearer elektrischer Netzwerke besagt das Norton-Theorem (auch Mayer-Norton-Theorem), dass jede mögliche Kombination von Spannungsquellen, Stromquellen und Widerständen bezüglich zweier Klemmen elektrisch äquivalent zu einer Parallelschaltung aus einer Stromquelle und einem Widerstand R ist. Diese Ersatzschaltung wird Norton-Äquivalent oder im deutschen Sprachraum Ersatzstromquelle genannt.

Jede elektrische Schaltung, die ausschließlich aus Spannungsquellen, Stromquellen und Widerständen besteht, kann in ein Norton-Äquivalent umgewandelt werden.

Berechnung des Norton-Äquivalents

Das Norton-Äquivalent besteht aus einem Widerstand R_No und einer Stromquelle I_No. Um die zwei Unbekannten R_No und I_No zu bestimmen, benötigt man zwei Gleichungen. Diese Gleichungen können auf verschiedene Art und Weise erstellt werden. Meistens gebraucht man jedoch folgende:

• Den Ausgangsstrom I_AB bei Kurzschluss bestimmen. Dieser Kurzschlussstrom ist der Norton-Äquivalentstrom I_No.

Um den Norton-Äquivalentwiderstand R_No zu bestimmen, gibt es verschiedene Methoden:

• Man ersetzt alle Spannungsquellen durch Kurzschlüsse und streicht alle Stromquellen (d.h. man ersetzt sie durch Open Circuits). Dann berechnet man den Ersatzwiderstand. Dieser ist gleich dem Norton-Äquivalentwiderstand.
• Wenn man die Leerlaufspannung U_AB kennt, benutzt man das ohmsche Gesetz, um R_No zu bestimmen:

$R_\mathrm{No} = {U_\mathrm{AB} \over I_\mathrm{No}} \,$

Beweis des Norton-Theorems

In diesem Artikel oder Abschnitt fehlen folgende wichtige Informationen: siehe Diskussion Du kannst Wikipedia helfen, indem du sie recherchierst und einfügst.

Der Beweis des Norton-Theorems basiert auf dem Überlagerungsprinzip.

Umwandlung zwischen Norton- und Thévenin-Äquivalent

Norton-Thévenin-Äquivalent-Umwandlung

Ein Norton-Äquivalent kann in ein Thévenin-Äquivalent umgewandelt werden anhand folgender Gleichungen:

$R_{Th} = R_{No} \,$

$V_{Th} = I_{No} R_{No} \,$

Frage zum Verständnis

Frage: »In zwei schwarzen Kistchen seien eine Stromquelle mit Parallelwiderstand und eine Spannungsquelle mit Serienwiderstand verborgen, so dass obige Gleichungen erfüllt sind. Kann man von außen feststellen, in welchem schwarzen Kistchen sich die Norton-Schaltung befindet?«

Antwort: Ja! Das Kistchen mit der Norton-Schaltung ist wärmer, denn es verbraucht dauernd die Leistung 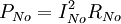$P_{No}=I_{No}^{2} R_{No}$. Die Thévenin-Schaltung verbraucht keine Leistung und wird deshalb nicht wärmer. Die Äquivalenz besteht also nur bezüglich der Ausgangsklemmen.

Diese Frage bewährt sich sehr, um in Kursen die Grenzen der Theorie von Norton- und Thévenin-Äquivalent zu verdeutlichen.

Erweiterung für Wechselstrom

Das Norton-Theorem kann auch auf Einfrequenz-Wechselstromsysteme verallgemeinert werden, indem man statt der ohmschen Widerstände Wechselstromwiderstände verwendet.

Historie

Das Norton-Theorem ist eine Erweiterung des Thévenin-Theorems. Es wurde 1926 gleichzeitig und unabhängig durch Hans Ferdinand Mayer (1895-1980) (bei Siemens & Halske) und Edward Lawry Norton (1898-1983) (bei Bell Labs) entdeckt. Mayer veröffentlichte seine Entdeckung in der Zeitschrift Telegraphen- und Fernsprech-Technik, Norton publizierte seine Entdeckung in einem internen Arbeitsbericht der Bell Labs. Dieses Theorem wird als Vereinfachungstechnik in der Schaltkreisanalyse verwendet.

Weblinks

• RWTH Aachen: Ersatzquellen. (PDF, 18,7 kB)

Siehe auch

• Elektrizität
• Thévenin-Theorem
• Kirchhoffsche Regeln
• Ohmsches Gesetz
• Überlagerungsprinzip
• Millman-Theorem
• Open circuit
• Kurzschluss (Strom)
• Spannungsteiler
• Parallelschaltung
• Reihenschaltung
• Stern-Dreieck-Transformation