Polarisationsweiche

Polarisationsapparat nach Nörrenberg für den Physikunterricht

Die Polarisation ist eine Eigenschaft optischer Wellen, welche die Richtung des Feldvektors des elektrischen Feldes beschreibt, und zwar im Vakuum oder in optisch-isotropen Medien (Gasen, Flüssigkeiten, kubischen Kristallen) in Bezug auf den Wellenvektor 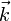$\vec k$. Sie beschränkt sich auf Transversalwellen (unter den angegebenen Voraussetzungen sind optische Wellen immer transversal). Bei nicht-kubischen Kristallen gibt es Abweichungen, die zu dem Phänomen der Doppelbrechung führen. Bei longitudinalen Wellenphänomenen, z. B. sog. Plasmaschwingungen oder Kompressions-Schallwellen, kann kein Polarisationsphänomen auftreten, da die Schwingung in Ausbreitungsrichtung (das ist die Richtung des k-Vektors) erfolgt. Optische Filter, mit denen sich Licht unterschiedlicher Polarisation beeinflussen lässt, werden Polarisatoren genannt.

Polarisationsarten

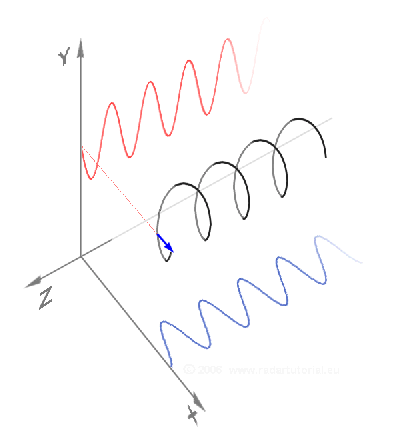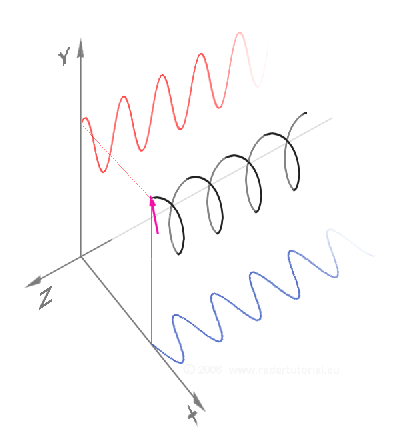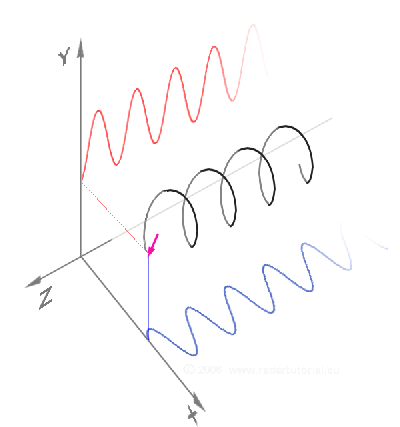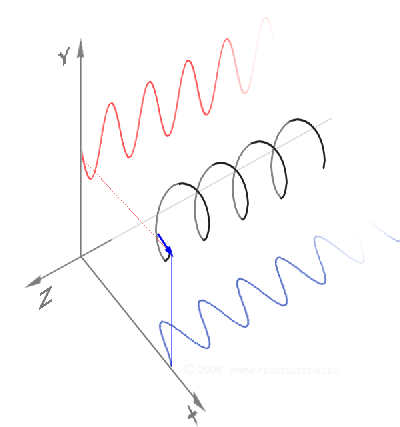
Eine Transversalwelle ist durch zwei Richtungen charakterisiert: Den Wellenvektor, der in Ausbreitungsrichtung zeigt, und den Feldvektor des elektrischen Feldes, der unter den angegebenen Voraussetzungen immer senkrecht auf dem Wellenvektor steht. Das lässt jedoch im dreidimensionalen Raum noch einen Rotationsfreiheitsgrad offen, nämlich die Rotation um den Wellenvektor. Man unterscheidet drei Arten von Polarisation, die man durch Richtung und Betrag des Feldvektors in einem festen Raumpunkt beschreiben kann:

• lineare Polarisation: Der Feldvektor zeigt immer in eine feste Richtung und die Auslenkung ändert bei Voranschreiten der Welle ihren Betrag und ihr Vorzeichen periodisch (mit fester Amplitude).
• zirkulare Polarisation (auch als drehende Polarisation bezeichnet): Der Feldvektor dreht sich bei Voranschreiten der Welle mit konstanter Winkelgeschwindigkeit um den Wellenvektor und ändert seinen Betrag dabei nicht.
• elliptische Polarisation: Der Feldvektor rotiert um den Wellenvektor und ändert dabei periodisch den Betrag. Die Spitze des Feldvektors beschreibt dabei eine Ellipse.

linear polarisierte Welle

zirkular polarisierte Welle

elliptisch polarisierte Welle

Lineare und zirkulare Polarisation können auch als Grenzfälle der elliptischen Polarisation aufgefasst werden, umgekehrt lässt sich aber auch jede elliptische Polarisation als eine Überlagerung einer linear- und einer zirkularpolarisierten Welle beschreiben.

Der Hintergrund dieser Tatsache ist, dass die Polarisation einer beliebigen Transversalwelle mit drei Größen vollständig beschrieben ist. Dies sind die Projektion des Feldvektors auf zwei orthogonale Achsen senkrecht zum Wellenvektor und der Phasenunterschied zwischen diesen beiden Projektionen. Die beiden orthogonalen Achsen können fest im Raum stehen (z. B. „horizontal“ oder „vertikal“), sie können aber auch um den Wellenvektor rotieren (rechts- oder linkszirkular).

Überlagerung

Jede beliebige Polarisation kann als Überlagerung zweier Basispolarisationen dargestellt werden. Häufig werden die folgenden beiden Varianten verwendet:

1. Zwei linear polarisierte Wellen, deren Polarisationsrichtungen senkrecht aufeinander stehen, werden überlagert. Abhängig von der Phasenbeziehung und dem Intensitätsverhältnis der beiden Wellen ergeben sich folgende Ausgangspolarisationen:
   • Bei verschwindender Phasendifferenz (oder einer Phasendifferenz, die einem Vielfachen von π entspricht) und unterschiedlicher Amplitude ist die Ausgangspolarisation linear und die Richtung hängt vom Amplitudenverhältnis ab.
   • Bei einem Phasenunterschied von π/2 und gleichen Intensitäten ist die Ausgangspolarisation zirkular.
   • In jedem anderen Fall ist die Ausgangspolarisation elliptisch.
2. Zwei zirkular polarisierte Wellen, eine rechts- und eine linksdrehend, werden überlagert. Abhängig von der Phasenbeziehung und dem Intensitätsverhältnis der beiden Wellen ergeben sich folgende Ausgangspolarisationen:
   • Bei gleichen Intensitäten und variabler Phasendifferenz ist die Ausgangspolarisation linear und die Richtung hängt von der Phasenlage der Basispolarisationen ab.
   • Wenn eine der Basispolarisationen eine verschwindende Amplitude hat, ist die Ausgangspolarisation die jeweils andere zirkulare Polarisation.
   • In jedem anderen Fall ist die Ausgangspolarisation elliptisch.

Die rote und die blaue Welle stellen linear polarisiertes, die schwarze zirkular polarisiertes Licht dar

Polarisation elektromagnetischer Wellen

Elektromagnetische Wellen, also auch Lichtwellen, sind – wie erwähnt – unter den angegebenen Voraussetzungen Transversalwellen. Zur Beschreibung ihrer Polarisation bezieht man sich üblicherweise auf das elektrische Feld und lässt das magnetische, das senkrecht auf dem elektrischen steht, außer Acht. In zirkularpolarisiertem Licht zeigen die Spins aller Photonen in dieselbe Richtung. Dennoch kann auch ein einzelnes Photon linearpolarisiert werden, indem zwei entgegengesetzt zirkularpolarisierte Zustände überlagert werden.

Polarisiertes Licht kann grundsätzlich erzeugt werden durch:

• Absorption
• Streuung
• Reflexion
• Doppelbrechung

Unpolarisiertes Licht kann nur durch Überlagerung inkohärenter Wellen erzeugt werden.

Die Messung der Polarisationsebene von Licht erfolgt durch Reflexion (Brewster-Winkel) oder Polarisationsfilter, bei Rundfunkwellen durch Dipole.

Erzeugung polarisierter Mikrowellen

Polarisations-Weiche Kathrein für zirkulare Links/Rechts Polarisation aus einem TV-SAT LNB KATHREIN  UAS 52 ca. 1987

Nachrichten- und Fernsehsatelliten nutzen entweder zwei verschiedene lineare Polarisationsebenen (horizontal/vertikal) oder zwei zirkulare Polarisationsrichtungen (links- oder rechtsdrehend), um die knappen, für den Satellitenfunk zur Verfügung stehenden Frequenzbänder besser ausnutzen zu können.

• Im Ku-Band (10,7–12,75 GHz) wird heute fast ausschließlich lineare Polarisation verwendet. Anfang der 1990er-Jahre sollten allerdings reine Fernsehsatelliten zirkular polarisiert senden (siehe: BSS Band).
• Im C-Band (3,7–4,2 GHz) sendeten dagegen bis vor kurzem fast alle Satelliten zirkular polarisiert, jedoch wird in letzter Zeit auch im C-Band lineare Polarisation häufiger verwendet.
• Von der Merkursonde MESSENGER ist bekannt, dass ihre Antennen die Signale zirkular polarisiert im X-Band senden.

Linear polarisierte Mikrowellen werden dadurch erzeugt, dass der Sendedipol entweder „horizontal“ oder „vertikal“ ausgerichtet ist. Die so erzeugten Mikrowellen sind in der Ebene polarisiert, in der sich der Sendedipol befindet. Zum Empfang der linear polarisierten Signale muss sich der Empfangsdipol in der Ebene befinden, in der die zu empfangende Welle schwingt.

Radiowellen niederer Frequenzen werden fast immer polarisiert abgestrahlt. Die Art der Polarisierung hängt von der Ausrichtung der Antenne ab. Sender im UHF/VHF-Bereich arbeiten – von Mobilfunksendern abgesehen – im Regelfall mit horizontaler Polarisation, da hierbei weniger Störungen auftreten. Im Kurzwellenbereich sind sowohl horizontale wie auch vertikale Polarisation üblich. Sender im Längst-, Lang- und Mittelwellenbereich arbeiten fast durchweg mit vertikaler Polarisation, da diese eine bessere Ausbreitung der Bodenwelle ermöglicht.

Zirkularpolarisation wird für Rundfunkzwecke nur selten angewandt. Sie wird für Steilstrahlantennen im Mittelwellenbereich manchmal verwendet.

Mathematische Beschreibung der Polarisation

Der Polarisationszustand kann durch die vierdimensionalen reellwertigen Stokes-Vektoren oder durch die zweidimensionalen komplexwertigen Jones-Vektoren beschrieben werden. Quasimonochromatisches Licht kann alternativ auch durch die Kohärenzmatrix beschrieben werden. Die Beschreibung der Wirkung eines polarisationsverändernden optischen Elementes erfolgt dann durch Multiplikation mit einer entsprechenden Müller-Matrix beziehungsweise einer Jones-Matrix.

Sichtbarkeit für Mensch und Tier

Entgegen der oft gehörten Meinung, der Mensch könne die Polarisationsrichtung des Lichts nicht erkennen, ist er dazu sehr wohl in der Lage (siehe Haidinger-Büschel). Ebenso sind einige Tierarten wie Fangschreckenkrebse dazu in der Lage^{[1] [2]}.

Einzelnachweise

1. ↑ www.fangschreckenkrebse.de
2. ↑ Englischer Wikipedia-Artikel zum Fangschreckenkrebs (englisch: Mantis Shrimp)

Weblinks

• Virtuelles Polarisationsmikroskop
• Polarisation bei atomaren Übergängen
• Animation von Zirkularwellen mit Polarisator
• JAVA-Applet zur Visualisierung von Polarisationszuständen

Videos

• Video vom „anderthalb Lexikon“ über Polarisation (langsame Verbindung; schnelle Verbindung)