- Pseudovektor
-
Ein Pseudovektor, auch Drehvektor, Axialvektor oder axialer Vektor genannt, ist in der Physik eine vektorielle Größe, die, wenn man das Spiegelbild des untersuchten physikalischen Systems bei einer Punktspiegelung betrachtet, ihre Richtung beibehält, während polare oder Schubvektoren in solchem Fall ihre Richtung umkehren.
Zum Beispiel wird die Winkelgeschwindigkeit eines Körpers auf einer Kreisbahn, weil sich der Drehsinn bei einer Punktspiegelung des Koordinatensystems nicht ändert, durch einen axialen Vektor beschrieben, während die Bahngeschwindigkeit in solchem Fall in die entgegengesetzte Richtung zeigt und daher durch einen polaren Vektor beschrieben wird.
Die Richtung eines axialen Vektors ist bezüglich einer Orientierung des Raumes, üblicherweise der rechtshändigen, definiert. Axialvektoren treten typischerweise auf, wenn ein physikalischer Zusammenhang durch das Kreuzprodukt (welches bei rechtshändigen Koordinatensystemen die Rechte-Hand-Regel verwendet) ausgedrückt wird.
Inhaltsverzeichnis
Definition
Transformationsverhalten unter einer Bewegung des Systems
Zu einem gegebenen physikalischen System betrachte man ein zweites, welches zu jedem Zeitpunkt aus dem ersten durch dieselbe räumliche Bewegung hervorgeht (d. h. durch eine längen- und winkeltreue Abbildung, keine Bewegung im kinematischen Sinne!). Dabei sind auch ungleichsinnige (orientierungsumkehrende) Bewegungen erlaubt. Zu einem festen Zeitpunkt t wird also ein Teilchen im ersten System, welches sich am Ort P(t) befindet, auf ein Teilchen am Ort P'(t) im bewegten System abgebildet. Masse und Ladung des Teilchens bleiben dabei unverändert. Für kontinuierliche Verteilungen heißt das, dass eine Dichte ρ auf eine Dichte ρ' mit ρ'(t,P') = ρ(t,P) abgebildet wird. Man sagt, eine physikalische Größe habe ein bestimmtes Transformationverhalten unter der Bewegung, wenn diese Transformation die physikalische Größe auf die entsprechende Größe im bewegten System abbildet. Zum Beispiel hat das bewegte Teilchen am Ort P' die transformierte Geschwindigkeit v', welche durch die Geschwindigkeit v des ursprünglichen Teilchens am Ort P bestimmt ist.
Axiale und polare Vektoren
Setzt sich die Bewegung nur aus Verschiebungen und Drehungen zusammen, so ist das Transformationsverhalten für alle vektoriellen Größen dieselbe. Betrachtet man dagegen den Fall einer Punktspiegelung im Raum am Zentrum PZ, d. h.
 , wobei
, wobei  und
und  die Ortsvektoren eines Teilchens und seines Spiegelbildes sind, so sind zwei Fälle zu unterscheiden. Ein polarer Vektor, wie etwa die Geschwindigkeit
die Ortsvektoren eines Teilchens und seines Spiegelbildes sind, so sind zwei Fälle zu unterscheiden. Ein polarer Vektor, wie etwa die Geschwindigkeit  des Teilchens, ist dadurch charakterisiert, dass er wie die Ortsvektoren transformiert:
des Teilchens, ist dadurch charakterisiert, dass er wie die Ortsvektoren transformiert:  . Ein axialer Vektor, wie etwa die Winkelgeschwindigkeit
. Ein axialer Vektor, wie etwa die Winkelgeschwindigkeit  des Teilchens, wird dagegen unter der Punktspiegelung auf sich selbst abgebildet:
des Teilchens, wird dagegen unter der Punktspiegelung auf sich selbst abgebildet:  . Die Eigenschaft einer vektoriellen Größe, axial oder polar zu sein, legt bereits das Transformationsverhalten unter einer beliebigen Bewegung fest. Denn jede Bewegung lässt sich durch eine Hintereinanderausführung von Translationen, Drehungen und Punktspiegelungen darstellen.
. Die Eigenschaft einer vektoriellen Größe, axial oder polar zu sein, legt bereits das Transformationsverhalten unter einer beliebigen Bewegung fest. Denn jede Bewegung lässt sich durch eine Hintereinanderausführung von Translationen, Drehungen und Punktspiegelungen darstellen.Aktive und passive Transformation
Diese Betrachtungen[1] zum Transformationsverhalten einer vektoriellen Größe unter einer aktiven Bewegung des Systems hat nichts zu tun mit dem Transformationsverhalten der Komponenten des Vektors unter einer gewöhnlichen Koordinatentransformation. Letzteres ist dasselbe für axiale und polare Vektoren, nämlich das von Komponenten eines Tensors vom Rang eins. Es handelt sich also um echte Vektoren im Sinne der Tensorrechnung, weswegen der Begriff Pseudovektor in diesem Zusammenhang irreführend ist. Tatsächlich gibt es Autoren[2][3], die diese unterschiedlichen Begriffe nicht klar trennen. Viele Autoren [4][5] beschreiben eine ungleichsinnige Bewegung des Systems als Koordinatentransformation bei gleichzeitiger Änderung der Orientierung, bezüglich welcher das Kreuzprodukt zu berechnen ist. Dies entspricht einer passiven Transformation, wobei der Beobachter die gleiche Transformation erfährt wie das Koordinatensystem. Anschaulich bedeutet das, dass die rechte Hand bei einer Punktspiegelung des Koordinatensystems zu einer linken Hand wird. Rechnerisch wird das realisiert durch die Einführung eines Pseudotensors, dessen Komponenten unabhängig von der Orientierung eines orthonormalen Koordinatensystems durch das Levi-Civita-Symbol gegeben sind. Dieser vollständig antisymmetrischen Pseudotensor (auch Tensordichte vom Gewicht -1 genannt) ist also kein Tensor. In diesem Sinne ist auch der Begriff Pseudovektor zu verstehen, welcher in dieser Betrachtung bei einer Punktspiegelung des Koordinatensystems seine Richtung ändert (dessen Komponenten dagegen unverändert bleiben). Diese passive Sichtweise liefert die gleichen Ergebnisse bezüglich der Unterscheidung axialer und polarer Vektoren wie die aktive.
Beispiele
- Für den Zusammenhang von Ortsvektor
 , Geschwindigkeit
, Geschwindigkeit  und Winkelgeschwindigkeit
und Winkelgeschwindigkeit  eines Teilchens gilt
eines Teilchens gilt  . Unter einer Punktspiegelung
. Unter einer Punktspiegelung  prüft man leicht nach, dass
prüft man leicht nach, dass  . Orts- und Geschwindigkeitvektor sind also Polarvektoren. Damit gilt für die Winkelgeschwindigkeit
. Orts- und Geschwindigkeitvektor sind also Polarvektoren. Damit gilt für die Winkelgeschwindigkeit  des gespiegelten Teilchens
des gespiegelten Teilchens  . Also muss
. Also muss  gelten, d. h. die Winkelgeschwindigkeit ist ein Axialvektor.
gelten, d. h. die Winkelgeschwindigkeit ist ein Axialvektor. - Aus der Formel für die Lorentzkraft
 folgt, dass das Magnetfeld
folgt, dass das Magnetfeld  ein axialer Vektor sein muss, denn die Kraft
ein axialer Vektor sein muss, denn die Kraft  ist zur Beschleunigung proportional und damit ein polarer Vektor.
ist zur Beschleunigung proportional und damit ein polarer Vektor. - Der Drehimpuls ist definiert als
 . Es folgt
. Es folgt  , also ist der Drehimpuls ein Axialvektor.
, also ist der Drehimpuls ein Axialvektor. - Die Wirbelstärke
 mit dem Nabla-Operator
mit dem Nabla-Operator  ist ein Axialvektor.
ist ein Axialvektor.
Rechenregeln
- Das Kreuzprodukt zweier polarer oder zweier axialer Vektoren ist ein Axialvektor.
- Das Kreuzprodukt aus einem polaren und einem axialen Vektor ist ein Polarvektor.
- Das Skalarprodukt zweier polarer oder zweier axialer Vektoren ist ein Skalar (d. h. behält sein Vorzeichen unter einer beliebigen Bewegung).
- Das Skalarprodukt aus einem polaren und einem axialen Vektor ist ein Pseudoskalar (d. h. ändert sein Vorzeichen unter einer Punktspiegelung).
Zusammenhang mit antisymmetrischen Tensoren
Einem axialen Vektor kann man über Hodge-Dualität einen antisymmetrischen Tensor zweiter Stufe zuordnen. In Koordinaten ausgedrückt gehört zu einem Vektor ai die 2-Form
 mit dem Levi-Civita-Symbol
mit dem Levi-Civita-Symbol  und unter Verwendung der Summenkonvention. Als Matrix geschrieben erhält man:
und unter Verwendung der Summenkonvention. Als Matrix geschrieben erhält man: .
.
Für das Magnetfeld B etwa erhält man auf diese Weise die räumlichen Komponenten des elektromagnetischen Feldstärketensors. Dieser Zusammenhang kann benutzt werden, um Größen wie den Drehimpuls für Räume der Dimension ungleich drei zu verallgemeinern. Nur im R3 hat eine antisymmetrische 2-Form genauso viele unabhängige Komponenten wie ein Vektor. Im R4 beispielsweise sind es nicht 4, sondern 6 unabhängige Komponenten.
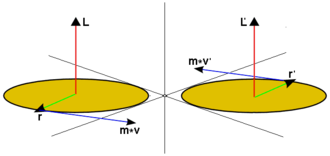
Beispiel: Spiegelung einer rotierenden Scheibe an einer Ebene
Betrachten wir das Beispiel einer rotierenden horizontalen Scheibe. Die Scheibe habe eine rote Oberseite und eine gelbe Unterseite. Die Rotation wird durch den Winkelgeschwindigkeitsvektor beschrieben. Nehmen wir an, die Rotationsrichtung sei so, dass der Winkelgeschwindigkeitsvektor von der roten Oberseite nach oben wegzeigt. Nun betrachten wir das horizontale Spiegelbild dieser rotierenden Scheibe. Die vertikalen Anteile von Orts- und Geschwindigkeitsvektoren haben sich umgekehrt, die Oberseite ist nun gelb und die Unterseite rot. Der Drehsinn dagegen bleibt erhalten. Also hat sich der Winkelgeschwindigkeitsvektor durch die Spiegelung nicht umgekehrt.
Einzelnachweise
- ↑ Richard P. Feynman, Robert B. Leighton, Matthew Sands: Lectures on physics. Vol. 1, Addison-Wesley, 1964, S. 52-6ff..
- ↑ axialer Vektor. In: Lexikon der Physik. Spektrum Akademischer Verlag, abgerufen am 23. Juli 2008: „Die Komponenten axialer Vektoren bleiben bei einer Spiegelung des Koordinatensystems, d.h. bei einer Vorzeichenumkehr aller drei Koordinaten, ungeändert;...“
- ↑ Eric W. Weisstein: Pseudovector. In: MathWorld - A Wolfram Web Resource. abgerufen am 23. Juli 2008: „A typical vector (...) is transformed to its negative under inversion of its coordinate axes.“
- ↑ Arnold Sommerfeld: Mechanik. In: Vorlesungen über Theoretische Physik. 8. Auflage. Band I, Harri Deutsch, 1994, ISBN 3-87144-374-3, S. 105.
- ↑ Herbert Goldstein, Charles Poole, John Safko: Classical mechanics. 3. Auflage. Addison-Wesley, 2000, S. 169.
Siehe auch
- Für den Zusammenhang von Ortsvektor
Wikimedia Foundation.