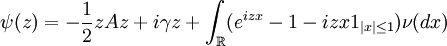- Levy-Prozess
-
Die Klasse der Lévy-Prozesse, benannt nach dem französischen Mathematiker Paul Lévy (1886-1971), fasst eine große Menge von stochastischen Prozessen zusammen, die durch die gemeinsame Eigenschaft der stationären, unabhängigen Zuwächse vereint werden. Lévy-Prozesse kommen überall dort zur Anwendung, wo die zeitliche Entwicklung einer Größe beschrieben werden soll, die zwar zufälligen, aber über die Zeit (in Verteilung) gleich bleibenden und voneinander unabhängigen Einflüssen ausgesetzt ist. Viele wichtige Prozesse wie der Wiener-Prozess oder der Poisson-Prozess sind Lévy-Prozesse.
Inhaltsverzeichnis
Definition
Sei
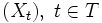 ein stochastischer Prozess über der Indexmenge T (meist
ein stochastischer Prozess über der Indexmenge T (meist 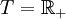 oder
oder 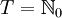 ). Man sagt, Xt habe unabhängige Zuwächse, wenn für alle
). Man sagt, Xt habe unabhängige Zuwächse, wenn für alle  die Zufallsvariablen
die Zufallsvariablen 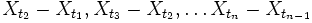 (die Zuwächse von Xt) unabhängig sind.
(die Zuwächse von Xt) unabhängig sind.Ist die Verteilung der Zuwächse über gleich langen Zeitintervallen dieselbe, d. h. gilt
so nennt man Xt einen Prozess mit stationären Zuwächsen.
Als Lévy-Prozesse bezeichnet man genau jene Prozesse Xt, die unabhängige und stationäre Zuwächse aufweisen.
Zeitdiskrete Lévy-Prozesse
Gilt speziell
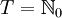 , so lässt sich die Klasse der Lévy-Prozesse sehr einfach charakterisieren: Es gibt nämlich für alle solchen Prozesse
, so lässt sich die Klasse der Lévy-Prozesse sehr einfach charakterisieren: Es gibt nämlich für alle solchen Prozesse 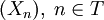 eine Darstellung
eine Darstellungwobei
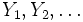 unabhängig und identisch wie X1 − X0 verteilt sind. Andererseits ist für jede beliebige Startverteilung X0, jede Verteilungsfunktion F und jede unabhängige Folge von Zufallsvariablen
unabhängig und identisch wie X1 − X0 verteilt sind. Andererseits ist für jede beliebige Startverteilung X0, jede Verteilungsfunktion F und jede unabhängige Folge von Zufallsvariablen 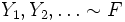 durch
durch 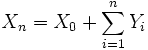 ein Lévy-Prozess X definiert. Im zeitdiskreten Fall ist ein Lévy-Prozess also im Prinzip nichts anderes als ein Random Walk mit beliebiger, aber gleich bleibender Sprungverteilung. Das einfachste Beispiel für einen zeitdiskreten Lévy-Prozess ist demnach auch der einfache, symmetrische Random Walk, bei dem 2(X1 − X0) − 1 symmetrisch Bernoulli-verteilt ist. Hier bewegt sich der Prozess X, startend bei X0 = 0 (f.s.), in jedem Schritt mit Wahrscheinlichkeit ½ um Eins nach oben, andernfalls um Eins nach unten.
ein Lévy-Prozess X definiert. Im zeitdiskreten Fall ist ein Lévy-Prozess also im Prinzip nichts anderes als ein Random Walk mit beliebiger, aber gleich bleibender Sprungverteilung. Das einfachste Beispiel für einen zeitdiskreten Lévy-Prozess ist demnach auch der einfache, symmetrische Random Walk, bei dem 2(X1 − X0) − 1 symmetrisch Bernoulli-verteilt ist. Hier bewegt sich der Prozess X, startend bei X0 = 0 (f.s.), in jedem Schritt mit Wahrscheinlichkeit ½ um Eins nach oben, andernfalls um Eins nach unten.Zeitstetige Lévy-Prozesse
 Ein Gamma-Prozess ist ein Lévy-Prozess, bei dem die Inkremente (Zuwächse) unabhängig und gammaverteilt sind. Dies ist möglich, da die Gammaverteilung unendlich teilbar ist. Man sieht sofort (support auf der positiven reellen Achse), dass der Prozess fast sicher wächst, er ist also ein subordinator. Der Prozess hat unendliche Aktivität und keine Diffusionskomponente. Die beiden zufälligen Pfade sind von Trajektorien von Gamma-Prozessen, mit den shape-Parametern 0.7 (rot) und 0.25 (blau)
Ein Gamma-Prozess ist ein Lévy-Prozess, bei dem die Inkremente (Zuwächse) unabhängig und gammaverteilt sind. Dies ist möglich, da die Gammaverteilung unendlich teilbar ist. Man sieht sofort (support auf der positiven reellen Achse), dass der Prozess fast sicher wächst, er ist also ein subordinator. Der Prozess hat unendliche Aktivität und keine Diffusionskomponente. Die beiden zufälligen Pfade sind von Trajektorien von Gamma-Prozessen, mit den shape-Parametern 0.7 (rot) und 0.25 (blau)Im Fall
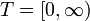 ist die Charakterisierung nicht mehr so leicht: so gibt es zum Beispiel keinen zeitstetigen Lévy-Prozess, bei dem X1 wie oben Bernoulli-Verteilt ist.
ist die Charakterisierung nicht mehr so leicht: so gibt es zum Beispiel keinen zeitstetigen Lévy-Prozess, bei dem X1 wie oben Bernoulli-Verteilt ist.Jedoch sind zeitstetige Lévy-Prozesse eng verwandt mit dem Begriff der unendlichen Teilbarkeit: Ist nämlich
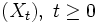 ein Lévy-Prozess, so ist X1 − X0 unendlich teilbar. Andererseits legt eine Startverteilung X0 und eine unendlich teilbare Zufallsvariable Y die Verteilung eines Lévy-Prozesses X durch X1 = X0 + Y eindeutig fest. Jedem Lévy-Prozess entspricht eine unendlich teilbare Verteilungsfunktion und umgekehrt.
ein Lévy-Prozess, so ist X1 − X0 unendlich teilbar. Andererseits legt eine Startverteilung X0 und eine unendlich teilbare Zufallsvariable Y die Verteilung eines Lévy-Prozesses X durch X1 = X0 + Y eindeutig fest. Jedem Lévy-Prozess entspricht eine unendlich teilbare Verteilungsfunktion und umgekehrt.Wichtige Beispiele für zeitstetige Lévy-Prozesse sind der Wiener-Prozess (auch Brownsche Bewegung genannt), bei dem die unendlich teilbare Zufallsvariable normalverteilt ist, oder der Poisson-Prozess, bei dem Y Poisson-verteilt ist. Doch auch viele andere Zufallsvariablen, beispielsweise die Gammaverteilung oder die Cauchy-Verteilung, können zur Konstruktion von Lévy-Prozessen herangezogen werden. Der Wiener-Prozess ist der einzige stetige Lévy-Prozess (neben dem deterministischen Prozess), d.h. aus der Stetigkeit eines Lévy-Prozesses folgt schon die Normalverteilung der Inkremente. Es existiert jedoch kein Lévy-Prozess mit gleichverteilten Zuständen.
Wichtig ist auch der Begriff der endlichen und unendlichen Aktivität: Gibt es in einem Intervall unendlich viele (und damit unendlich kleine) Sprünge oder nicht? Auskunft darüber gibt auch das Lévy-Maß.
Weiterhin sind subordinators wichtig, dh Lévy-Prozesse mit fast sicher wachsenden (ansteigenden) Pfaden. Ein Beispiel dafür ist der Gamma-Prozess. Die Differenz von zwei Gamma-Prozessen wird als variance-gamma-process bezeichnet.
Weitere Definition
Ein stochastischer Prozess
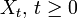 über einem Wahrscheinlichkeitsraum
über einem Wahrscheinlichkeitsraum 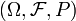 heißt Lévy-Prozess, wenn
heißt Lévy-Prozess, wenn- X0 = 0,
- Xt unabhängige und stationäre Zuwächse hat und
- Xt stochastisch stetig ist, d. h. für beliebige
 und
und 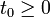 gilt
gilt
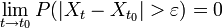 .
.
Lévy-Chintschin Formel
Für jeden Lévy-Prozess Xt mit dem charakteristischen Tripel (A, ν, γ) gilt:
mit
Benannt ist diese Darstellung der charakteristischen Funktion eines Lévy-Prozesses nach Paul Lévy und Alexander Jakowlewitsch Chintschin.
Wichtige Eigenschaften
- Mit Hilfe der charakteristischen Funktion des Prozesses
-
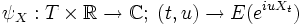
lässt sich ein einfaches Kriterium für Lévy-Prozesse aufstellen: so ist ein stochastischer Prozess genau dann ein Lévy-Prozess, wenn Funktionen k, l existieren, sodass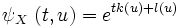
gilt.
- Die Erwartungswertfunktion eines Lévy-Prozesses Xt ist linear in t, d. h.
-
- E(Xt) = E(X0) + tE(X1 − X0). Analog gilt für die Varianz
- Var(Xt) = Var(X0) + tVar(X1 − X0) (vorausgesetzt die entsprechenden Momente existieren zum Zeitpunkt 1). Für die Kovarianzfunktion gilt
- Cov(Xs,Xt) = Var(Xmin(s,t)) = Var(X0) + min(s,t)Var(X1 − X0).
- Falls E(X1 − X0) = 0 gilt, so ist (Xt) ein Martingal.
Literatur
- J. Bertoin: Lévy Processes. Cambridge Tracts in Mathematics, Vol. 121, Cambridge University Press 2002, ISBN 0-52164-632-4
- A. E. Kyprianou: Introductory Lectures on fluctuations of Lévy process with applications. Universitext, Springer.
- Philip E. Protter: Stochastic Integration and Differential Equations. Springer, Berlin 2003, ISBN 3-540-00313-4
- Rama Cont, Peter Tankov: Financial Modelling with Jump Processes. Chapman & Hall, 2003, ISBN 1-584-88413-4
- Ken-iti Sato: Lévy Processes and Infinitely Divisible Distributions. Cambridge studies in advanced mathematics, 1999, ISBN 0-521-55302-4
Weblinks
Wikimedia Foundation.

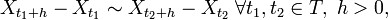
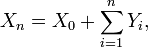

![E[e^{i z X_t}]=e^{t\psi(z)}](/pictures/dewiki/52/4b6345fb4f20a84e8b4b3c3ca4e5969d.png)