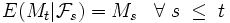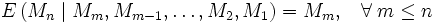Submartingal

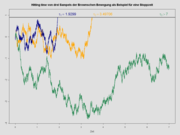
Pfade von zwei kompensierten zusammengesetzten Poisson-Prozessen. Die Intensität (Sprunghäufigkeit) des blauen Prozesses ist mit 2.4 genau vier mal so hoch wie die des roten Prozesses. Im gezeichneten Intervall [0,35] springt der blaue Prozess 66 mal, der rote 16 mal, also cira vier mal so oft. Bei beiden Prozessen sind die Sprünge normalverteilt mit Mittel 0.25. Diese Sprünge nach oben werden durch den negativen Drift genau so ausgegleichen (kompensiert), dass beide Prozesse Martingale sind. Da der blaue Prozess öfter nach oben springt ist sein negativer Drift stärker.

In der Wahrscheinlichkeitstheorie ist ein Martingal ein stochastischer Prozess, in dem der Erwartungswert einer Beobachtung gleich dem Wert der vorigen Beobachtung ist.

In die Mathematik wurden Martingale von Paul Pierre Lévy eingeführt.

Definition

Sei 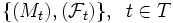$\{(M_t),(\mathcal{F}_t)\}, \;\; t \in T$ ein stochastischer Prozess mit einer beliebigen, geordneten Indexmenge T.

M_t heißt ein Martingal bezüglich einer Filtrierung 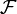$\mathcal{F}$, wenn M_t für jedes 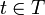$t \in T$ integrierbar ist, an die Filtrierung 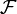$\mathcal{F}$ adaptiert ist und

$E(M_t| \mathcal{F}_s) = M_s \;\;\; \forall\; s\; \le\; t$

(P-)fast sicher gilt.

Die letzte Bedingung kann so interpretiert werden, dass ein Martingal ein faires Spiel ist, da der Erwartungswert einer zukünftigen Beobachtung gleich der letzten getätigten Beobachtung ist. Wenn der Wert eines Martingals zum Zeitpunkt s bekannt ist, dann ist der Erwartungswert zukünftiger Beobachtungen nicht von Werten abhängig, die vor s beobachtet wurden.

Damit gilt noch nicht zwingend die Markov-Eigenschaft, dass die Verteilung von M_t lediglich von M_s abhängt. Zum Beispiel kann die Streuung des Martingals auch von Beobachtungen vor s abhängen.

Definition im Falle der natürlichen Filtrierung

Im zeitdiskreten Fall wird ein stochastischer Prozess 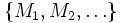$\{M_1, M_2, \ldots\}$ als Martingal bezüglich seiner natürlichen Filtrierung bezeichnet, wenn der bedingte Erwartungswert einer zukünftigen Beobachtung

$E \left( M_n \mid M_{m},M_{m-1} , \ldots,M_2,M_1 \right)=M_m, \;\;\;\forall\; m \le n$

gleich dem zuletzt beobachteten Wert ist.

Ist 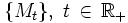$\{M_t\}, \; t \, \in \, \mathbb{R}_+ \$ ein zeitstetiger stochastischer Prozess, so lautet obige Bedingung

$E(M_t| {M_s};s \in [a,b])=M_b\;\;\; \forall\; a \;\le\; b\; \le\; t$.

Sub- und Supermartingal

Als Submartingal bezeichnet man einen stochastischen Prozess X_t, der im Gegensatz zum Martingal tendenziell steigt:

$E(X_t\,|\,X_s = x) \geq x \;\; \forall \; s<t$

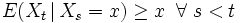
Dementsprechend ist ein Supermartingal ein stochastischer Prozess X_t, der tendenziell fällt:

$E(X_t\,|\,X_s = x)\leq x\;\; \forall \; s<t$

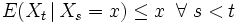
Exponentialmartingal

Ist die quadratische Variation 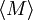$\langle M\rangle$ eines stetigen beschränkten Martingals M_t (oder eines mit endlichen exponentiellen Momenten) endlich, so ist der stochastische Prozess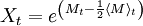

$X_t=e^{\left(M_t-\frac{1}{2}\langle M\rangle_t\right)}$

ebenfalls ein Martingal und heißt Exponentialmartingal von M_t

Beispiele für Martingale

Wiener-Prozess als Beispiel für ein Martingal

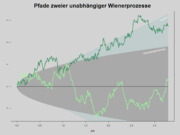
• Ein Wiener-Prozess W_t ohne Drift ist ein Martingal, ebenso wie eine geometrische brownsche Bewegung ohne Drift.
• Jedes gestoppte Martingal ist wieder ein Martingal.
• Ein Poisson-Prozess mit Rate λ, der um seine Drift bereinigt wird, also 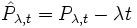$\hat P_{\lambda,t}=P_{\lambda,t}-\lambda t$, ist ein Martingal.
• Ein symmetrischer Random Walk, bei dem die Wahrscheinlichkeit für eine Aufwärtsbewegung ebenso wie für eine Abwärtsbewegung 1 / 2 ist, ist ein Martingal.

Gestoppte Brownsche Bewegung als Beispiel für ein Martingal

• Nach dem Lemma von Itō gilt: Jedes Itō-Integral (mit beschränktem Integranden) ist ein Martingal. Nach dem Ito'schen Martingaldarstellungssatz lässt sich umgekehrt jedes Martingal (sogar jedes lokale Martingal) bezüglich einer von einer Brown'schen Bewegung erzeugten Filtration als Ito-Integral bezüglich eben dieser Brown'schen Bewegung darstellen.
• Jedes stetige Martingal ist entweder von unendlicher Variation oder konstant.

Herkunft des Wortes

Das Wort stammt aus dem Provenzalischen und ist über das Französische in die Weltsprache der Mathematik übergegangen. Das Martingal bezeichnet im Reitsport einen optionalen Teil der Pferdeausrüstung, der das Pferd daran hindern soll, den Kopf nach oben zu reißen und zu steigen. Der Name Martingal bezieht sich auf die französische Stadt Martigues im Departement Bouches du Rhone am Rande der Camargue, wo dieser Hilfszügel erfunden wurde.

Seit dem 18. Jahrhundert steht Martingal auch für eine Strategie im Glücksspiel (vgl. Martingalespiel), bei der nach einem verlorenen Spiel der Einsatz erhöht, im einfachsten Fall verdoppelt wird, so dass im Falle unerschöpflichen Vermögens, unerschöpflicher Zeit, und Nichtexistenz eines Höchsteinsatzes sicherer Gewinn eintritt. ^[1]

Siehe auch

• Lokales Martingal
• Semimartingal

Belege und Quellen

1. ↑ H. Bauer, Wahrscheinlichkeitstheorie; deGruyter,1991